Генератор случайных чисел, который производит распределение по закону мощности?
Я пишу некоторые тесты для приложения командной строки c++ Linux. Я хотел бы создать кучу целых чисел с распределением power-law/long-tail. Это означает, что я получаю некоторые цифры очень часто, но большинство из них относительно редко.
В идеале было бы просто несколько магических уравнений, которые я мог бы использовать с rand() или одной из случайных функций stdlib. Если нет, простой в использовании кусок C / C++ было бы здорово.
спасибо!
4 ответов
этой страница в Wolfram MathWorld обсуждает, как получить распределение мощности из равномерного распределения (что обеспечивает большинство генераторов случайных чисел).
короткий ответ (вывод по приведенной выше ссылке):
x = [(x1^(n+1) - x0^(n+1))*y + x0^(n+1)]^(1/(n+1))
здесь y единый вариативной, n распределение власти, x0 и x1 определите диапазон распределения и x ваша власть-закон распространяется вариативной.
если вы знаете распределение, которое хотите (называемое функцией распределения вероятности (PDF)), и оно правильно нормализовано, вы можете интегрировать его, чтобы получить кумулятивную функцию распределения (CDF), а затем инвертировать CDF (если это возможно), чтобы получить преобразование, которое вам нужно от uniform [0,1] рассылки по вашему желанию.
Итак, вы начинаете с определения распределения, которое хотите.
P = F(x)
(для x в [0,1]) затем интегрировано, чтобы дать
C(y) = \int_0^y F(x) dx
если этот можно перевернуть вы получите
y = F^{-1}(C)
так называем rand() и подключите результат как C в последней строке и используйте y.
этот результат называется фундаментальной теоремой выборки. Это хлопот из-за требования нормализации и необходимости аналитически инвертировать функцию.
попеременно вы можете использовать метод отклонения: бросьте число равномерно в желаемом диапазоне, затем бросьте другое число и сравните с PDF в месте indeicated на свой первый бросок. Отклонить, если второй бросок превышает PDF. Как правило, неэффективно для PDF-файлов с большим количеством областей с низкой вероятностью, таких как с длинными хвостами...
промежуточный подход включает в себя инвертирование CDF грубой силой: вы храните CDF как таблицу поиска и выполняете обратный поиск, чтобы получить результат.
настоящий вонючка здесь это просто x^-n дистрибутивы не являются нормируемыми в диапазоне [0,1], поэтому вы не можете использовать теорема отсчетов. Попробуйте (x+1)^-n вместо этого...
Я не могу прокомментировать математику, необходимую для создания распределения закона мощности (у других сообщений есть предложения), но я бы предложил вам ознакомиться с объектами случайных чисел стандартной библиотеки TR1 C++ в <random>. Они обеспечивают больше функциональности, чем std::rand и std::srand. Новая система определяет модульный API для генераторов, двигателей и распределений и поставляет кучу пресетов.
включенные пресеты распределения являются:
uniform_intbernoulli_distributiongeometric_distributionpoisson_distribution-
binomial_distribution uniform_realexponential_distributionnormal_distributiongamma_distribution
когда вы определяете ваше распределение закона силы, вы должны мочь заткнуть его внутри с существующими генераторами и двигателями. Книга Расширения Стандартной Библиотеки C++ Пит Бекер многие глава о <random>.
вот статья о том, как создавать другие дистрибутивы (с примерами для Коши, Хи-квадрат, Student t и Snedecor F)
Я просто хотел провести реальное моделирование в качестве дополнения к (по праву) принято отвечать. Хотя в R код настолько прост, что является (псевдо)-псевдо-кодом.
одна крошечная разница между формула вольфрама MathWorld в принятом ответе и других, возможно, более распространенных, уравнениях есть тот факт, что показатель степенного закона n (который обычно обозначается как "Альфа") не несет явный отрицательный знак. Так выбрали Альфа-значение должно быть отрицательным, и обычно между 2 и 3.
x0 и x1 подставка для нижнего и верхнего пределов распространения.
так вот:
x1 = 5 # Maximum value
x0 = 0.1 # It can't be zero; otherwise X^0^(neg) is 1/0.
alpha = -2.5 # It has to be negative.
y = runif(1e5) # Number of samples
x = ((x1^(alpha+1) - x0^(alpha+1))*y + x0^(alpha+1))^(1/(alpha+1))
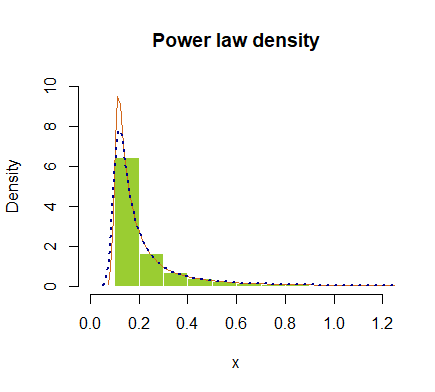
hist(x, prob = T, breaks=40, ylim=c(0,10), xlim=c(0,1.2), border=F,
col="yellowgreen", main="Power law density")
lines(density(x), col="chocolate", lwd=1)
lines(density(x, adjust=2), lty="dotted", col="darkblue", lwd=2)
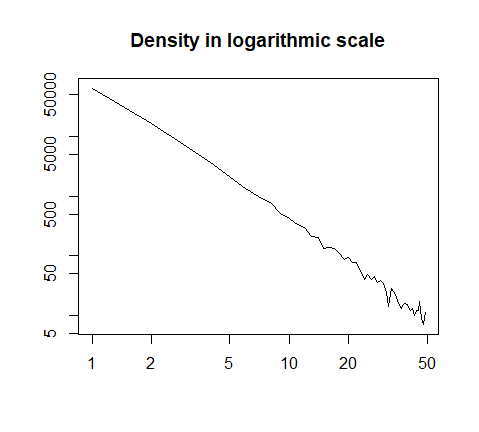
или нанесены в логарифмическом масштабе:
h = hist(x, prob=T, breaks=40, plot=F)
plot(h$count, log="xy", type='l', lwd=1, lend=2,
xlab="", ylab="", main="Density in logarithmic scale")
вот краткое изложение данных:
> summary(x)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.1000 0.1208 0.1584 0.2590 0.2511 4.9388