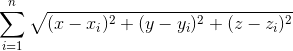Геометрическая медиана многомерных точек
У меня есть массив точек 3D:
a = np.array([[2., 3., 8.], [10., 4., 3.], [58., 3., 4.], [34., 2., 43.]])
Как я могу вычислить геометрическая медиана из этих пунктов?
3 ответов
я реализовал алгоритм Иегуды Варди и Куньхуэй Чжана для геометрической медианы, описанный в их статье "многомерная L1-медиана и связанная с ней глубина данных". Все векторизовано в numpy, поэтому должно быть очень быстро. Я не использовал веса-только невесомые точки.
import numpy as np
from scipy.spatial.distance import cdist, euclidean
def geometric_median(X, eps=1e-5):
y = np.mean(X, 0)
while True:
D = cdist(X, [y])
nonzeros = (D != 0)[:, 0]
Dinv = 1 / D[nonzeros]
Dinvs = np.sum(Dinv)
W = Dinv / Dinvs
T = np.sum(W * X[nonzeros], 0)
num_zeros = len(X) - np.sum(nonzeros)
if num_zeros == 0:
y1 = T
elif num_zeros == len(X):
return y
else:
R = (T - y) * Dinvs
r = np.linalg.norm(R)
rinv = 0 if r == 0 else num_zeros/r
y1 = max(0, 1-rinv)*T + min(1, rinv)*y
if euclidean(y, y1) < eps:
return y1
y = y1
в дополнение к условиям лицензии SO по умолчанию, я выпускаю код выше под лицензией zlib, если вы так предпочитаете.
расчет геометрических медиана итерационный алгоритм Weiszfeld реализуется в Python в этой суть или в функции ниже скопировано с OpenAlea программное обеспечение (лицензия CeCILL-C),
import numpy as np
import math
import warnings
def geometric_median(X, numIter = 200):
"""
Compute the geometric median of a point sample.
The geometric median coordinates will be expressed in the Spatial Image reference system (not in real world metrics).
We use the Weiszfeld's algorithm (http://en.wikipedia.org/wiki/Geometric_median)
:Parameters:
- `X` (list|np.array) - voxels coordinate (3xN matrix)
- `numIter` (int) - limit the length of the search for global optimum
:Return:
- np.array((x,y,z)): geometric median of the coordinates;
"""
# -- Initialising 'median' to the centroid
y = np.mean(X,1)
# -- If the init point is in the set of points, we shift it:
while (y[0] in X[0]) and (y[1] in X[1]) and (y[2] in X[2]):
y+=0.1
convergence=False # boolean testing the convergence toward a global optimum
dist=[] # list recording the distance evolution
# -- Minimizing the sum of the squares of the distances between each points in 'X' and the median.
i=0
while ( (not convergence) and (i < numIter) ):
num_x, num_y, num_z = 0.0, 0.0, 0.0
denum = 0.0
m = X.shape[1]
d = 0
for j in range(0,m):
div = math.sqrt( (X[0,j]-y[0])**2 + (X[1,j]-y[1])**2 + (X[2,j]-y[2])**2 )
num_x += X[0,j] / div
num_y += X[1,j] / div
num_z += X[2,j] / div
denum += 1./div
d += div**2 # distance (to the median) to miminize
dist.append(d) # update of the distance evolution
if denum == 0.:
warnings.warn( "Couldn't compute a geometric median, please check your data!" )
return [0,0,0]
y = [num_x/denum, num_y/denum, num_z/denum] # update to the new value of the median
if i > 3:
convergence=(abs(dist[i]-dist[i-2])<0.1) # we test the convergence over three steps for stability
#~ print abs(dist[i]-dist[i-2]), convergence
i += 1
if i == numIter:
raise ValueError( "The Weiszfeld's algoritm did not converged after"+str(numIter)+"iterations !!!!!!!!!" )
# -- When convergence or iterations limit is reached we assume that we found the median.
return np.array(y)
кроме того, вы можете использовать реализацию C, упомянутую в этом ответ, и интерфейс его к python С, например,ctypes.
проблема может быть легко аппроксимирована minimize модуль scipy. В этом модуле он предоставляет различные алгоритмы оптимизации, от nelder-mead до newton-CG. Алгоритм нельдера-МИД особенно полезен, если вы не хотите возиться с производными высокого порядка, ценой потери некоторой точности. Тем не менее, вам просто нужно знать функцию, которая будет сведена к минимуму для алгоритм нелдера-МИД на работу.
теперь, ссылаясь на тот же массив на вопросы, если мы используем метод @orlp, мы получим следующее:
geometric_median(a)
# array([12.58942481, 3.51573852, 7.28710661])
для метода Nelder-mead вы увидите ниже. Минимизируемая функция-это функция расстояния от всех точек, т. е.
вот код:
from scipy.optimize import minimize
x = [point[0] for point in a]
y = [point[1] for point in a]
z = [point[2] for point in a]
x0 = np.array([sum(x)/len(x),sum(y)/len(y), sum(z)/len(z)])
def dist_func(x0):
return sum(((np.full(len(x),x0[0])-x)**2+(np.full(len(x),x0[1])-y)**2+(np.full(len(x),x0[2])-z)**2)**(1/2))
res = minimize(dist_func, x0, method='nelder-mead', options={'xtol': 1e-8, 'disp': True})
res.x
# array([12.58942487, 3.51573846, 7.28710679])
обратите внимание, что я использую для обозначения всех точек в качестве начальных значений для alogrithm. Результат довольно близок к методу @orlp, который является более точным. Как я уже упоминал, вы жертвуете немного, но все равно получаете неплохо аппроксимирует.
производительность алгоритма Nelder Mead
Для этого я создал test_array С 10000 входами пунктов от нормального распределения центризованного на 3.2. Поэтому геометрическая медиана должна быть достаточно близка к [3.2, 3.2, 3.2].
np.random.seed(3)
test_array = np.array([[np.random.normal(3.2,20),
np.random.normal(3.2,20),
np.random.normal(3.2,20)] for i in np.arange(10000)])
для метода @orlp,
%timeit geometric_median(test_array)
# 12.1 ms ± 270 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
# array([2.95151061, 3.14098477, 3.01468281])
для нелдера-МИДа,
%timeit res.x
# 565 ms ± 14.8 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
# array([2.95150898, 3.14098468, 3.01468276])
метод@orlp очень быстр пока мед Nelder не плох. Однако метод Nelder mead является общим в то время как @orlp специфичен для геометрической медианы. Метод, который вы хотели бы выбрать, будет зависеть от вашей цели. Если вы просто хотите приблизительный, я выберу Нелдера непринужденно. Если вы хотите быть точным, метод @orlp является более быстрым и точным.