градиентный спуск с использованием python и numpy
def gradient(X_norm,y,theta,alpha,m,n,num_it):
temp=np.array(np.zeros_like(theta,float))
for i in range(0,num_it):
h=np.dot(X_norm,theta)
#temp[j]=theta[j]-(alpha/m)*( np.sum( (h-y)*X_norm[:,j][np.newaxis,:] ) )
temp[0]=theta[0]-(alpha/m)*(np.sum(h-y))
temp[1]=theta[1]-(alpha/m)*(np.sum((h-y)*X_norm[:,1]))
theta=temp
return theta
X_norm,mean,std=featureScale(X)
#length of X (number of rows)
m=len(X)
X_norm=np.array([np.ones(m),X_norm])
n,m=np.shape(X_norm)
num_it=1500
alpha=0.01
theta=np.zeros(n,float)[:,np.newaxis]
X_norm=X_norm.transpose()
theta=gradient(X_norm,y,theta,alpha,m,n,num_it)
print theta
моя тета из вышеуказанного кода -100.2 100.2, но он должен быть!--2--> в matlab, который является правильным.
4 ответов
Я думаю, что ваш код слишком сложный, и ему нужно больше структуры, потому что иначе вы потеряетесь во всех уравнениях и операциях. В конце концов эта регрессия сводится к четырем операциям:
- вычислить гипотезу h = X * theta
- вычислить убыток = h-y и, возможно, квадрат стоимости (убыток^2) / 2m
- вычислить градиент = X ' * loss / m
- обновить параметры theta = Theta-alpha * градиент
в вашем случае, я думаю, вы спутали m С n. Вот!--2--> обозначает количество примеров в обучающей выборке, а не ряд особенностей.
давайте посмотрим на мой вариант кода:
import numpy as np
import random
# m denotes the number of examples here, not the number of features
def gradientDescent(x, y, theta, alpha, m, numIterations):
xTrans = x.transpose()
for i in range(0, numIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis - y
# avg cost per example (the 2 in 2*m doesn't really matter here.
# But to be consistent with the gradient, I include it)
cost = np.sum(loss ** 2) / (2 * m)
print("Iteration %d | Cost: %f" % (i, cost))
# avg gradient per example
gradient = np.dot(xTrans, loss) / m
# update
theta = theta - alpha * gradient
return theta
def genData(numPoints, bias, variance):
x = np.zeros(shape=(numPoints, 2))
y = np.zeros(shape=numPoints)
# basically a straight line
for i in range(0, numPoints):
# bias feature
x[i][0] = 1
x[i][1] = i
# our target variable
y[i] = (i + bias) + random.uniform(0, 1) * variance
return x, y
# gen 100 points with a bias of 25 and 10 variance as a bit of noise
x, y = genData(100, 25, 10)
m, n = np.shape(x)
numIterations= 100000
alpha = 0.0005
theta = np.ones(n)
theta = gradientDescent(x, y, theta, alpha, m, numIterations)
print(theta)
сначала я создаю небольшой случайный набор данных, который должен выглядеть так:
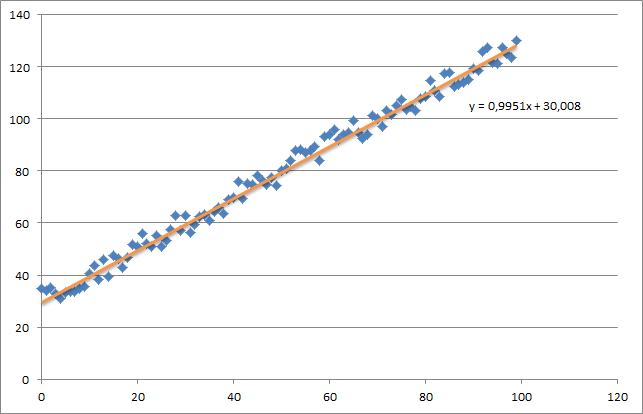
как вы можете видеть, я также добавил сгенерированную линию регрессии и формулу, которая была рассчитана превосходить.
вам нужно позаботиться о интуиции регрессии, используя градиентный спуск. Когда вы выполняете полный пакетный проход над данными X, вам нужно уменьшить M-потери каждого примера до одного обновления веса. В этом случае это среднее значение суммы по градиентам, таким образом, деление на m.
следующее, что вам нужно позаботиться о том, чтобы отслеживать сходимость и регулировать скорость обучения. В этом отношении вы всегда должны отслеживать свою стоимость каждую итерацию, может быть, даже сюжет.
если вы запустите мой пример, тета возвращен будет выглядеть так:
Iteration 99997 | Cost: 47883.706462
Iteration 99998 | Cost: 47883.706462
Iteration 99999 | Cost: 47883.706462
[ 29.25567368 1.01108458]
что на самом деле довольно близко к уравнению, которое было вычислено excel (y = x + 30). Обратите внимание, что когда мы передали смещение в первый столбец, первое тета-значение обозначает вес смещения.
ниже вы можете найти мою реализацию градиентного спуска для задачи линейной регрессии.
сначала вы вычисляете градиент, как X.T * (X * w - y) / N и обновите текущую тэту с помощью этого градиента одновременно.
- X: feature matrix
- y: целевые значения
- w: веса / значения
- N: размер тренировочного набора
вот python код:
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import random
def generateSample(N, variance=100):
X = np.matrix(range(N)).T + 1
Y = np.matrix([random.random() * variance + i * 10 + 900 for i in range(len(X))]).T
return X, Y
def fitModel_gradient(x, y):
N = len(x)
w = np.zeros((x.shape[1], 1))
eta = 0.0001
maxIteration = 100000
for i in range(maxIteration):
error = x * w - y
gradient = x.T * error / N
w = w - eta * gradient
return w
def plotModel(x, y, w):
plt.plot(x[:,1], y, "x")
plt.plot(x[:,1], x * w, "r-")
plt.show()
def test(N, variance, modelFunction):
X, Y = generateSample(N, variance)
X = np.hstack([np.matrix(np.ones(len(X))).T, X])
w = modelFunction(X, Y)
plotModel(X, Y, w)
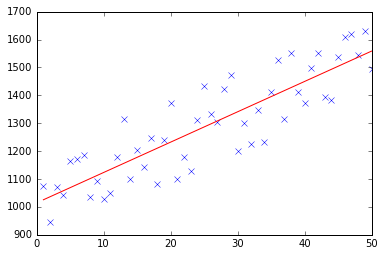
test(50, 600, fitModel_gradient)
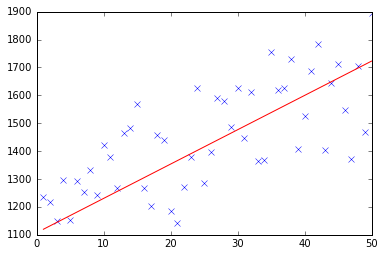
test(50, 1000, fitModel_gradient)
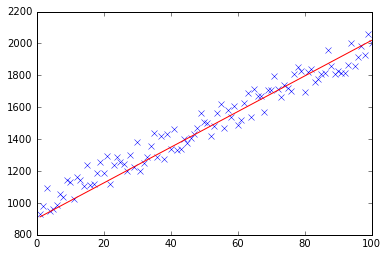
test(100, 200, fitModel_gradient)
Я знаю, что этот вопрос уже был ответом, но я сделал некоторое обновление функции GD:
### COST FUNCTION
def cost(theta,X,y):
### Evaluate half MSE (Mean square error)
m = len(y)
error = np.dot(X,theta) - y
J = np.sum(error ** 2)/(2*m)
return J
cost(theta,X,y)
def GD(X,y,theta,alpha):
cost_histo = [0]
theta_histo = [0]
# an arbitrary gradient, to pass the initial while() check
delta = [np.repeat(1,len(X))]
# Initial theta
old_cost = cost(theta,X,y)
while (np.max(np.abs(delta)) > 1e-6):
error = np.dot(X,theta) - y
delta = np.dot(np.transpose(X),error)/len(y)
trial_theta = theta - alpha * delta
trial_cost = cost(trial_theta,X,y)
while (trial_cost >= old_cost):
trial_theta = (theta +trial_theta)/2
trial_cost = cost(trial_theta,X,y)
cost_histo = cost_histo + trial_cost
theta_histo = theta_histo + trial_theta
old_cost = trial_cost
theta = trial_theta
Intercept = theta[0]
Slope = theta[1]
return [Intercept,Slope]
res = GD(X,y,theta,alpha)
эта функция уменьшает Альфа над итерацией, делая функцию слишком сходящейся быстрее см. оценка линейной регрессии с градиентным спуском (самый крутой спуск) для примера в R. я применяю ту же логику, но в Python.
следуя реализации @thomas-jungblut в python, я сделал то же самое для Octave. Если вы нашли что-то не так, пожалуйста, дайте мне знать, и я исправлю+обновление.
данные поступают из txt-файла со следующими строками:
1 10 1000
2 20 2500
3 25 3500
4 40 5500
5 60 6200
подумайте об этом как о очень грубой выборке для функций [количество спален] [mts2] и последней колонки [цена аренды], которую мы хотим предсказать.
вот реализация Октавы:
%
% Linear Regression with multiple variables
%
% Alpha for learning curve
alphaNum = 0.0005;
% Number of features
n = 2;
% Number of iterations for Gradient Descent algorithm
iterations = 10000
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% No need to update after here
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
DATA = load('CHANGE_WITH_DATA_FILE_PATH');
% Initial theta values
theta = ones(n + 1, 1);
% Number of training samples
m = length(DATA(:, 1));
% X with one mor column (x0 filled with '1's)
X = ones(m, 1);
for i = 1:n
X = [X, DATA(:,i)];
endfor
% Expected data must go always in the last column
y = DATA(:, n + 1)
function gradientDescent(x, y, theta, alphaNum, iterations)
iterations = [];
costs = [];
m = length(y);
for iteration = 1:10000
hypothesis = x * theta;
loss = hypothesis - y;
% J(theta)
cost = sum(loss.^2) / (2 * m);
% Save for the graphic to see if the algorithm did work
iterations = [iterations, iteration];
costs = [costs, cost];
gradient = (x' * loss) / m; % /m is for the average
theta = theta - (alphaNum * gradient);
endfor
% Show final theta values
display(theta)
% Show J(theta) graphic evolution to check it worked, tendency must be zero
plot(iterations, costs);
endfunction
% Execute gradient descent
gradientDescent(X, y, theta, alphaNum, iterations);