хэш-функция, обеспечивающая уникальный uint из целочисленной пары координат

Кантор перечисление пар

   n = ((x + y)*(x + y + 1)/2) + y

может быть интересно, так как он ближе всего к вашему исходному canvaswidth * y + x, но будет работать для любого x или y. Но для хэша int32 реального мира, а не для отображения пар целых чисел на целые числа, вам, вероятно, лучше с Бит-манипуляцией, такой как Боб Дженкин mix и называя это с x, y и солью.

Как Эмиль, но обрабатывает 16-битные переполнения в x таким образом, который производит меньше столкновений и принимает меньше инструкций для вычисления:

hash = ( y << 16 ) ^ x;

ваш "идеал" невозможно.

вы хотите отображение (x, y)- > i, где x, y и i-все 32-разрядные величины, которые гарантированно не генерируют повторяющиеся значения i.

вот почему: предположим, что существует функция hash (), так что hash (x, y) дает разные целочисленные значения. Существует 2^32 (около 4 миллиардов) значений для x и 2^32 значения y. Таким образом, хэш(x, y) имеет 2^64 (около 16 миллионов триллионов) возможных результатов. Но есть только 2^32 возможных значения в 32-битном int, поэтому результат hash () не будет вписываться в 32-битный int.

см. также http://en.wikipedia.org/wiki/Counting_argument

Как правило, вы всегда должны проектировать свои структуры данных для борьбы с коллизиями. (Если ваши хэши не очень длинные (по крайней мере, 128 бит), очень хорошо (используйте криптографические хэш-функции), и вы чувствуете себя счастливым).

возможно?

hash = ((y & 0xFFFF) << 16) | (x & 0xFFFF);

работает до тех пор, пока x и y могут храниться как 16-битные целые числа. Не знаю, сколько столкновений это вызывает для больших целых чисел. Одна из идей может заключаться в том, чтобы все еще использовать эту схему, но объединить ее со схемой сжатия, например, взять модуль 2^16.

Если вы можете сделать a = ((y & 0xffff)

uint32_t hash( uint32_t a)
    a = (a ^ 61) ^ (a >> 16);
    a = a + (a << 3);
    a = a ^ (a >> 4);
    a = a * 0x27d4eb2d;
    a = a ^ (a >> 15);
    return a;
}

таким образом, вы получаете случайный результат, а не высокие биты из одного измерения и низкие биты из другого.

в соответствии с вашим случаем использования можно использовать дерева квадрантов и замените точки строкой имен ветвей. Это на самом деле разреженное представление для точек и потребуется пользовательская структура Quadtree, которая расширяет холст, добавляя ветви при добавлении точек с холста, но это позволяет избежать конфликтов, и у вас будут преимущества, такие как быстрый поиск ближайшего соседа.

Если вы уже используете языки или платформы, которые все объекты (даже примитивные, такие как целые числа) имеют встроенные хэш-функции (языки платформы Java, такие как Java, языки платформы .NET, такие как C#. И другие, такие как Python, Ruby и т. д. ). Вы можете использовать встроенные значения хэширования в качестве строительного блока и добавить свой "вкус хэширования" в микс. Например:

// C# code snippet 
public class SomeVerySimplePoint { 

public int X;
public int Y;

public override int GetHashCode() {
   return ( Y.GetHashCode() << 16 ) ^ X.GetHashCode();
}

}

а также с тестовыми случаями, такими как" предопределенный набор миллионов точек", работающий против каждого возможного хэширования сравнение алгоритмов для различных аспектов, таких как время вычисления, требуемая память, количество ключевых столкновений и крайние случаи (слишком большие или слишком маленькие значения) могут быть удобны.

можно сделать

a >= b ? a * a + a + b : a + b * b

взято отсюда.

это работает для пунктов в положительной плоскости. Если ваши координаты тоже могут быть в отрицательной оси, то вам придется сделать:

A = a >= 0 ? 2 * a : -2 * a - 1;
B = b >= 0 ? 2 * b : -2 * b - 1;
A >= B ? A * A + A + B : A + B * B;

но ограничить выход до uint вам придется сохранить верхнюю границу для ваших входов. а если так, то получается, что вы знаете границы. Другими словами, в программировании непрактично писать функцию, не имея представления о целочисленном введите ваши входы и выходы, и если да, то определенно будет нижняя граница и верхняя граница для каждого целочисленного типа.

public uint GetHashCode(whatever a, whatever b)
{
    if (a > ushort.MaxValue || b > ushort.MaxValue || 
        a < ushort.MinValue || b < ushort.MinValue)
    {    
        throw new ArgumentOutOfRangeException();
    }

    return (uint)(a * short.MaxValue + b); //very good space/speed efficiency
    //or whatever your function is.
}

если вы хотите, чтобы выход был строго uint для неизвестного диапазона входных данных, то будет разумное количество столкновений в зависимости от этого диапазона. Я бы предложил иметь функцию, которая может переполняться, но unchecked. Решение Эмиля великолепно, в C#:

return unchecked((uint)((a & 0xffff) << 16 | (b & 0xffff))); 

посмотреть отображение двух целых чисел в одно, уникальным и детерминированным способом для множества вариантов..

хеш Фибоначчи работает очень хорошо для целых пар

множитель 0x9E3779B9

другие размеры слова 1 / phi = (sqrt(5)-1)/2 * 2^W раунд до odd

А1 + А2*множитель

Это даст очень разные значения для близких пар

Я не знаю о результате со всеми парами!--1-->

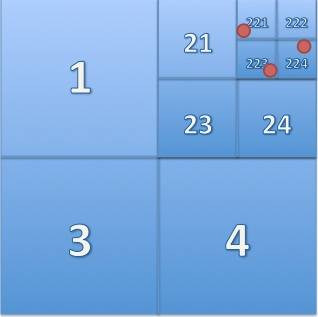
вы можете рекурсивно разделить плоскость XY на ячейки, а затем разделить эти ячейки на подэлементы и т. д.

Густаво Нимейер изобрел в 2008 году свою систему геокодирования Geohash.

подробнее:

https://en.wikipedia.org/wiki/Geohash https://aws.amazon.com/fr/blogs/mobile/geo-library-for-amazon-dynamodb-part-1-table-structure/ https://github.com/awslabs/dynamodb-geo