Интерполяция / масштабирование билинейных изображений-пример расчета
Я хотел бы спросить вас о некоторых деталях билинейной интерполяции / масштабирования. Предположим, что у нас есть такая матрица:
|100 | 50 |
|70 | 20 |
это изображение в оттенках серого 2 x 2. Теперь я хотел бы масштабировать его в два раза, и моя матрица выглядит так:
| 100 | f1 | 50 | f2 |
| f3 | f4 | f5 | f6 |
| 70 | f7 | 20 | f8 |
Итак, если мы хотим вычислить f4, расчет определяется как
f1 = 100 + 0.5(50 - 100) = 75
f7 = 70 + 0.5(20 - 70) = 45
и наконец:
f4 = 75 + 0.5(45 - 75) = 60
однако я не могу понять, какие вычисления правильны для Ф3 или f1
делаем ли мы билинейное масштабирование в каждом направлении отдельно? Следовательно, это означало бы, что:
f3 = 100 + 0.5(70 - 100) = 85
f1 = 100 + 0.5(50 - 100) = 75
кроме того, как я должен относиться f2, f6, f8. Эти точки просто копируются, как в алгоритме ближайшего соседа?
1 ответов
я хотел бы указать вам на эту очень проницательную графику из Википедии, которая иллюстрирует, как сделать билинейную интерполяцию для одной точки:
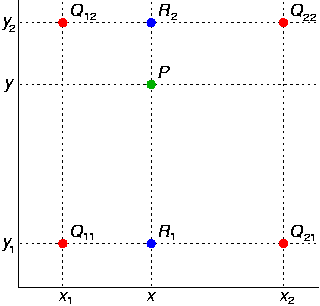
источник: Википедия
как вы можете видеть, четыре красные точки чем знаменит. Эти моменты вы знаете перед рукой и P это точка, которую мы хотим интерполировать. Таким образом, мы должны сделать два шага (как вы указали в ваших сообщениях.) Чтобы справиться с x координата (горизонтальная), мы должны вычислить, что интерполированное значение является строкой мудрой для верхней строки красных точек и нижней строки красных точек. Это приводит к двум синим точкам R1 и R2. Чтобы справиться с y координата (вертикальная), мы используем две синие точки и интерполируем вертикально, чтобы получить окончательный P точка.
при изменении размера изображения, даже если мы визуально не видим, что я собираюсь сказать, но представьте что это изображение 3D сигнала f. Каждая точка в матрице на самом деле является 3D-координатой, где расположение столбца равно x значением, расположение строки y значение и z значение-это значение количества / оттенков серого самой матрицы. Поэтому делаю z = f(x,y) значение матрицы в точке (x,y) в матрице. В нашем случае, поскольку вы имеете дело с изображениями, каждый стоимостью (x,y) - целые числа, которые идут от 1 до строки / столбцы, как у нас, в зависимости от того, какое измерение вы смотрите.
поэтому, учитывая координату, которую вы хотите интерполировать в (x,y), и учитывая красные координаты на изображении выше, которые мы называем их x1,y1,x2,y2 в соответствии с диаграммой-в частности, с соглашением диаграммы и ссылкой на то, как доступны изображения:x1 = 1, x2 = 2, y1 = 2, y2 = 1 синий координатами R1 и R2 вычисляются с помощью столбца интерполяции 1D, используя одну и ту же строку, обе точки совпадают on:
R1 = f(x1,y1) + (x - x1)/(x2 - x1)*(f(x2,y1) - f(x1,y1))
R2 = f(x1,y2) + (x - x1)/(x2 - x1)*(f(x2,y2) - f(x1,y2))
важно отметить, что (x - x1) / (x2 - x1) это вес / доля из того, сколько смеси выход состоит из двух значений, видимых в f(x1,y1) и f(x2,y1) на R1 или f(x1,y2) и f(x2,y2) на R2. В частности, x1 является отправной точкой и (x2 - x1) разница в x значения. Вы можете проверить, что подстановка x1 as x дает нам 0, а x2 as x дает нам 1. Этот вес колеблется между [0,1] который необходим для вычислений для работы.
следует отметить, что происхождение изображения находится в левом верхнем углу и так (1,1) в левом верхнем углу. Как только вы найдете R1 и R2 можно найти P путем интерполяции строки мудрый:
P = R2 + (y - y2)/(y2 - y1)*(R1 - R2)
опять (y - y2) / (y2 - y1) обозначьте пропорцию / смесь того, сколько R1 и R2 свой вклад в конечный результат P. Таким образом, вы из расчета f5 правильно, потому что вы использовали четыре известные точки: верхний левый-100, верхний правый-50, нижний левый-70 и нижний правый-20. В частности, если вы хотите вычислить f5, это означает, что (x,y) = (1.5,1.5) потому что мы на полпути между 100 и 50 из-за того, что вы масштабируете изображение на два. Если вы подключите эти значения к приведенному выше вычислению, вы получите значение 60, как и ожидалось. Веса для обоих вычислений также приведут к 0.5, которым это то, что вы получили в своих расчетах, и это то, что мы ожидаем.
если вы вычисляете f1, что соответствует (x,y) = (1.5,1) и если вы подставите это в приведенное выше уравнение, вы увидите, что (y - y2)/(y2 - y1) дает вам 0 или вес равен 0, и поэтому то, что вычисляется, просто R2, соответствующий линейной интерполяции только по верхней строке. Аналогично, если мы вычислили f7, это означает, что мы хотим интерполировать на (x,y) = (1.5,2). В этом случае, вы увидите, что (y - y2) / (y2 - y1) is 1 или вес 1 и поэтому P = R2 + (R1 - R2), что упрощает до R1 и является линейной интерполяцией только по нижней строке.
теперь есть случай f3 и f5. Оба они соответствуют (x,y) = (1,1.5) и (x,y) = (2,1.5) соответственно. Подставляя эти значения в R1 и R2 и P для обоих случаев дайте:
f3
R1 = f(1,2) + (1 - 1)/(2 - 1)*(f(2,2) - f(1,2)) = f(1,2)
R2 = f(1,1) + (1 - 1)/(2 - 1)*(f(1,2) - f(1,1)) = f(1,1)
P = R1 + (1.5 - 1)*(R1 - R2) = f(1,2) + 0.5*(f(1,2) - f(1,1))
P = 70 + 0.5*(100 - 70) = 85
f5
R1 = f(1,2) + (2 - 1)/(2 - 1)*(f(2,2) - f(1,2)) = f(2,2)
R2 = f(1,1) + (2 - 1)/(2 - 1)*(f(1,2) - f(1,1)) = f(1,2)
P = R1 + (1.5 - 1)*(R1 - R2) = f(2,2) + 0.5*(f(2,2) - f(1,2))
P = 20 + 0.5*(50 - 20) = 35
так что это нам говорит? Это означает, что вы интерполируете только по y-направлению. Это очевидно, когда мы смотрим на P. Более тщательное изучение расчетов P для каждого f3 и f5, вы видите, что мы рассматриваем значения только вдоль вертикального направления.
таким образом, если вы хотите однозначного ответа, f1 и f7 найдены путем интерполяции вдоль x / направление столбца только вдоль той же строки. f3 и f5 найдены путем интерполяции y / направление строки вдоль того же столбца. f4 использует смесь f1 и f7 для вычисления конечного значения, как вы уже видели.
чтобы ответить на ваш последний вопрос, f2, f6 и f8 заполняется на основе личных предпочтений. Эти значения считаются за пределами, с x и y значения как 2.5 и это вне нашего [1,2] сетка для (x,y). В MATLAB реализация этого по умолчанию заключается в заполнении любых значений за пределами определенных границ, чтобы быть не-числом (NaN), но иногда люди экстраполируют с помощью линейной интерполяции, копируют значения границ или выполняют некоторые сложные дополнения, такие как симметричное или круговое заполнение. Это зависит от того, в какой ситуации вы находитесь, но нет правильного и окончательного ответа о том, как заполнить f2, f6 и f8 - все зависит от вашего приложения и то, что делает самое разумное для тебя.
в качестве бонуса мы можем проверить правильность моих вычислений в MATLAB. Сначала определим сетку (x,y) точки в [1,2] диапазон, затем измените размер изображения так, чтобы оно было в два раза больше, где мы указываем разрешение 0,5 на точку, а не 1. Я собираюсь назвать вашу определенную матрицу A:
A = [100 50; 70 20]; %// Define original matrix
[X,Y] = meshgrid(1:2,1:2); %// Define original grid of points
[X2,Y2] = meshgrid(1:0.5:2.5,1:0.5:2.5) %// Define expanded grid of points
B = interp2(X,Y,A,X2,Y2,'linear'); %// Perform bilinear interpolation
оригинал (x,y) сеть точек выглядит так:
>> X
X =
1 2
1 2
>> Y
Y =
1 1
2 2
расширенная сетка для расширения размер матрицы в два раза больше выглядит как:
>> X2
X2 =
1.0000 1.5000 2.0000 2.5000
1.0000 1.5000 2.0000 2.5000
1.0000 1.5000 2.0000 2.5000
1.0000 1.5000 2.0000 2.5000
>> Y2
Y2 =
1.0000 1.0000 1.0000 1.0000
1.5000 1.5000 1.5000 1.5000
2.0000 2.0000 2.0000 2.0000
2.5000 2.5000 2.5000 2.5000
B вывод с помощью X и Y в качестве исходной сетки точек и X2 и Y2 - это точки, которые мы хотим интерполировать.
получаем:
>> B
B =
100 75 50 NaN
85 60 35 NaN
70 45 20 NaN
NaN NaN NaN NaN
