Иррациональное представление чисел на любом языке программирования?
кто-нибудь знает о иррациональном типе представления числа/объекте/классе/что угодно в любой язык программирования?
все предложения приветствуются.
проще говоря, если у меня есть два иррациональных объекта, оба представляющих квадратный корень из пяти, и я умножаю эти объекты, я хочу вернуть целое число пять, а не плавать 4 точечных лотов 9s.
в частности, мне нужно, чтобы представление могло собирать термины, а не просто разрешать каждый раз к целому числу / float. Например, если я хочу добавить квадратный корень из пяти к одному, я не хочу, чтобы он возвращал некоторое приближение integer/float, я хочу, чтобы он возвращал объект, который я могу добавить/умножить с другим иррациональным объектом, так что я могу сказать объекту разрешить в самое позднее время, чтобы минимизировать ошибку приближения float.
спасибо!
7 ответов
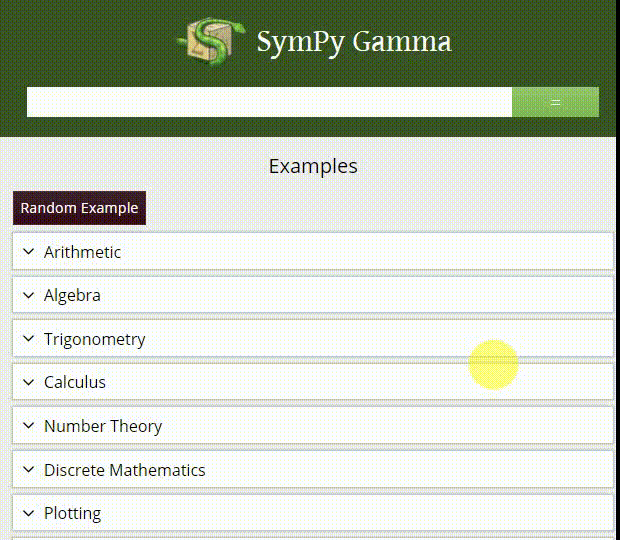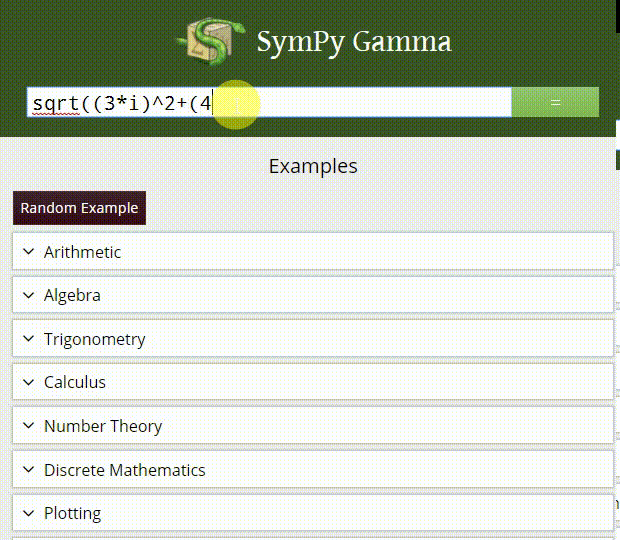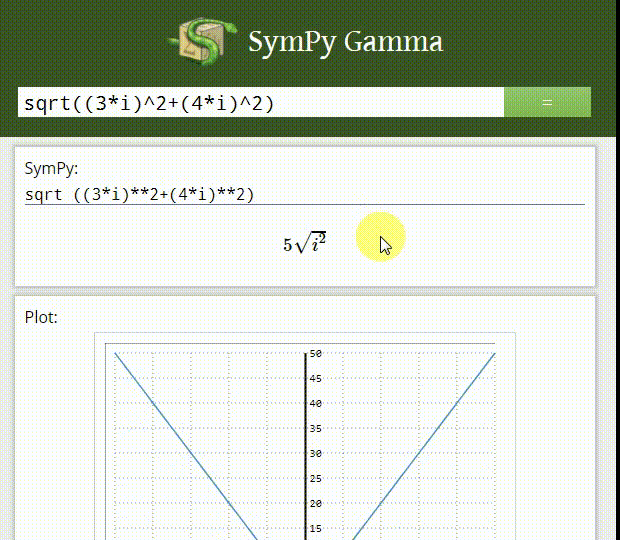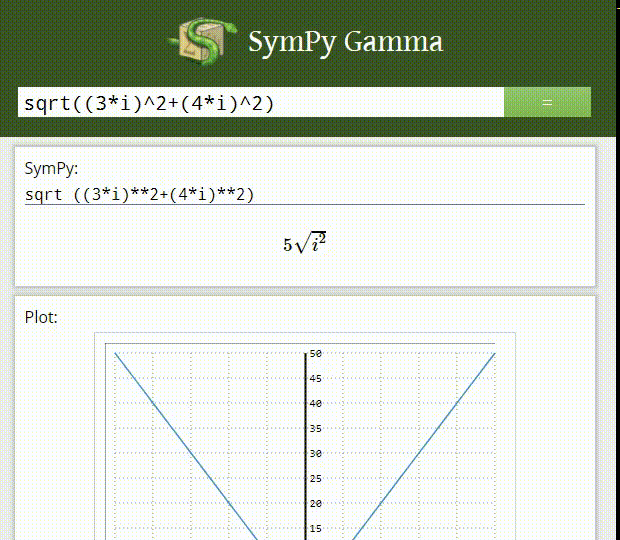
то, что вы ищете называется символьной математики. Вы можете попробовать некоторую систему компьютерной алгебры, такую как Maxima, Maple или Mathematica. Для этой цели также существуют библиотеки, например SymPy библиотека для Python.
можно попробовать sympy поскольку вы, похоже, после символических вычислений и поддаетесь использованию Python.
похоже, что уже упоминалось SymPy было бы самым подходящим способом - поскольку вы можете делать то, что вам нужно, и не требовать, чтобы ваше программное обеспечение было написано на специальном языке, таком как математические продукты, упомянутые.
С другой стороны, если вы не хотите вводить дополнительные зависимости, а ваши иррациональные случаи ограничены умножениями квадратных корней, в Python это легко задача:
class Irrational(float):
def __new__(cls, base, radix=1):
self = float.__new__(cls, base ** (1.0/radix))
self.base = base
self.radix = radix
return self
def __mul__(self, other):
if isinstance(other, Irrational) and other.radix == self.radix:
return Irrational(self.base * other.base, self.radix)
return float.__mul__(self, other)
пример:
>>> a = Irrational(5,2)
>>> a
2.2360679774997898
>>> a * Irrational(5,2)
5.0
Вы можете продолжить его дальше и включить операции ohter и угловые случаи. Но для выражений compes вы скоро поймете, что вам все равно придется использовать символическую математику.
для компиляции некоторых вещей, которые другие сказали, а также добавить несколько решений для других языков...
C++
Пиранья
попробуйте пиранью bluescarni "библиотека компьютерной алгебры"
// Include the standard I/O header.
#include <iostream>
// Include the global Piranha header.
#include <piranha/piranha.hpp>
// Import the names from the Piranha namespace.
using namespace piranha;
int main()
{
// Piranha initialisation.
init();
// Print the rational number 4/3 to screen.
std::cout << rational{4, 3} << '\n';
}
также Python обертка ("Pyranha") доступна.
SymEngine
SymEngine еще один с++-символическую математическая библиотека, с обертками для Python, Рубин, Юлия и Хаскелл. SymEngine прекрасно интегрируется с SymPy и Sage, как для Python.
Java
SymJa
попробуйте библиотеку Symja axkr
>>> sin(30*degree)
1/2
>>> sin(pi/2)
1
>>> a+a+4*b^2+3*b^2
2*a+7*b^2
кроме того, вы можете использовать языка Jython и SymPy in Ява.
Python
SymPy
как уже упоминалось, SymPy-это переход к символической математике в Python:
Рубин
символическое
Brainopia это является символической математической библиотекой (без внешних зависимостей) для Руби:
0 * x # => 0
2 + x + 1 # => x + 3
-(x-y) + 2*x # => x + y
(x**2)**3 / x # => x**5
Symbolic::Math.cos(x**2).diff(x)
# => -2*(sin(x**2))*x
Symbolic::Math.cos(x).taylor(x,0,3)
# => -0.5*x**2+1.0
пожалуйста, не стесняйтесь редактировать или изменять этот ответ с другими библиотеками символической математики. как правило, я не включил никаких математических библиотек "произвольной точности", потому что это не то же самое, что бесконечной точностью библиотека символической математики. Я также не включил устаревшие пакеты, которые не были обновлены в последнее время.
фундаментальный числовой тип в Matlab является матрицей сложных поплавков. В частности, если вы вводите x = 1, то, что вы действительно назначаете x, является матрицей 1x1 с ее [0,0] элементом, равным 1+0i.
в ruby есть http://flt.rubyforge.org/ который дает вам то, что вы хотите, я верю.
Я помню, что MathMorph в Smalltalk имеет представление для алгебраических чисел (которое включает радикалы) как корень многочлена одной переменной с целыми коэффициентами, лежащими в определенном интервале.
Вы найдете интересные приложения теоремы штурмаhttp://en.wikipedia.org/wiki/Sturm%27s_theorem
Вам придется немного погуглить и покопаться в старых архивах, хотя MathMorph-старый проект...