Исключить выбросы из расчета коэффициента корреляции
предположим, что у нас есть два числовых вектора x и y. Коэффициент корреляции Пирсона между x и y дано
cor (x, y)
как я могу автоматически рассматривать только подмножество x и y в расчет (скажем 90%), чтобы максимизировать коэффициент корреляции?
5 ответов
если вы действительно хотите сделать это (удалить наибольшие (абсолютные) остатки), затем мы можем использовать линейную модель для оценки решения наименьших квадратов и связанных остатков, а затем выбрать средний n% данных. Вот пример:
во-первых, генерировать фиктивные данные:
require(MASS) ## for mvrnorm()
set.seed(1)
dat <- mvrnorm(1000, mu = c(4,5), Sigma = matrix(c(1,0.8,1,0.8), ncol = 2))
dat <- data.frame(dat)
names(dat) <- c("X","Y")
plot(dat)
Далее, мы приспосабливаем линейную модель и извлекаем остатки:
res <- resid(mod <- lm(Y ~ X, data = dat))
на quantile() функция может дать нам необходимые квантили остатки. Вы предложили сохранить 90% данных, поэтому нам нужны верхние и нижние 0,05 квантиля:
res.qt <- quantile(res, probs = c(0.05,0.95))
выберите те наблюдения с остатками в середине 90% данных:
want <- which(res >= res.qt[1] & res <= res.qt[2])
затем мы можем визуализировать это, причем красные точки будут теми, которые мы сохраним:
plot(dat, type = "n")
points(dat[-want,], col = "black", pch = 21, bg = "black", cex = 0.8)
points(dat[want,], col = "red", pch = 21, bg = "red", cex = 0.8)
abline(mod, col = "blue", lwd = 2)
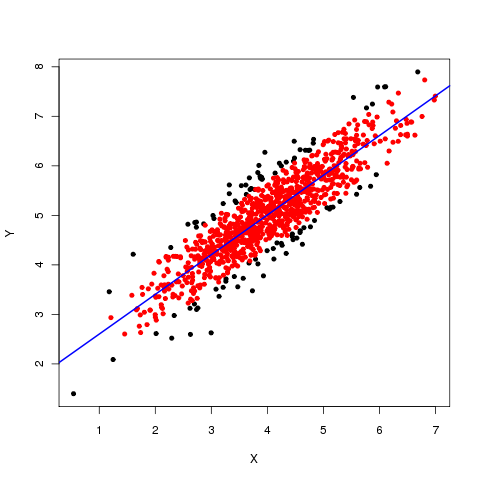
корреляции для полных данных и выбранного подмножества:
> cor(dat)
X Y
X 1.0000000 0.8935235
Y 0.8935235 1.0000000
> cor(dat[want,])
X Y
X 1.0000000 0.9272109
Y 0.9272109 1.0000000
> cor(dat[-want,])
X Y
X 1.000000 0.739972
Y 0.739972 1.000000
имейте в виду, что здесь мы могли бы бросить из совершенно хороших данных, потому что мы просто выбираем 5% с наибольшими положительными остатками и 5% с наибольшим отрицательным. Альтернативой является выбор 90% с наименьшим абсолютное невязок:
ares <- abs(res)
absres.qt <- quantile(ares, prob = c(.9))
abswant <- which(ares <= absres.qt)
## plot - virtually the same, but not quite
plot(dat, type = "n")
points(dat[-abswant,], col = "black", pch = 21, bg = "black", cex = 0.8)
points(dat[abswant,], col = "red", pch = 21, bg = "red", cex = 0.8)
abline(mod, col = "blue", lwd = 2)
С этим немного другим подмножеством корреляция немного ниже:
> cor(dat[abswant,])
X Y
X 1.0000000 0.9272032
Y 0.9272032 1.0000000
другой момент заключается в том, что даже тогда мы выбрасываем хорошие данные. Возможно, вы захотите взглянуть на расстояние Кука как на показатель силы выбросов, и отбросьте только те значения, которые превышают определенный порог расстояния Кука. Википедия имеет информацию о расстоянии Кука и предлагаемых порогах. The cooks.distance() функция может использоваться для извлечения значений из mod:
> head(cooks.distance(mod))
1 2 3 4 5 6
7.738789e-04 6.056810e-04 6.375505e-04 4.338566e-04 1.163721e-05 1.740565e-03
и если вы вычислите порог(ы), предложенный в Википедии, и удалите только те, которые превышают порог. Для этих данных:
> any(cooks.distance(mod) > 1)
[1] FALSE
> any(cooks.distance(mod) > (4 * nrow(dat)))
[1] FALSE
ни одно из расстояний повара не превышает предлагаемых порогов (неудивительно, учитывая, как я сгенерировал данные.)
сказав Все это, почему вы хотите это сделать? Если вы просто пытаетесь избавиться от данных, чтобы улучшить корреляцию или создать значительную связь, это звучит немного подозрительно и немного похоже на выемку данных.
используя method = "spearman" на cor будет робастно к загрязнению и легко для того чтобы снабдить в виду того что оно только включает заменять cor(x, y) С cor(x, y, method = "spearman").
повторяя анализ Прасада, но используя вместо этого корреляции Спирмена, мы обнаруживаем, что корреляция Спирмена действительно устойчива к загрязнению здесь, восстанавливая лежащую в основе нулевую корреляцию:
set.seed(1)
# x and y are uncorrelated
x <- rnorm(1000)
y <- rnorm(1000)
cor(x,y)
## [1] 0.006401211
# add contamination -- now cor says they are highly correlated
x <- c(x, 500)
y <- c(y, 500)
cor(x, y)
## [1] 0.995741
# but with method = "spearman" contamination is removed & they are shown to be uncorrelated
cor(x, y, method = "spearman")
## [1] -0.007270813
это, возможно, уже было очевидно для ОП, но просто чтобы убедиться... Вы должны быть осторожны, потому что пытается maxmimize корреляция, возможно, на самом деле, как правило,включить останцы. (@Gavin коснулся этого момента в своем ответе/комментариях.) Я бы первый удаление выбросов, затем вычисление корреляции. В более общем плане мы хотим вычислить корреляцию, которая устойчива к выбросам (и в R есть много таких методов).
чтобы наглядно проиллюстрировать это, давайте создадим два вектора x и y, которые являются некоррелированными:
set.seed(1)
x <- rnorm(1000)
y <- rnorm(1000)
> cor(x,y)
[1] 0.006401211
теперь давайте добавим точку выброса (500,500):
x <- c(x, 500)
y <- c(y, 500)
теперь соотношение любой подмножество, включающее точку выброса, будет близко к 100%, а корреляция любого достаточно большого подмножества, исключающего выброс, будет близка к нулю. В частности,
> cor(x,y)
[1] 0.995741
если вы хотите оценить "истинную" зависимость, которая не чувствительна к выбросам, вы можете попробовать robust пакет:
require(robust)
> covRob(cbind(x,y), corr = TRUE)
Call:
covRob(data = cbind(x, y), corr = TRUE)
Robust Estimate of Correlation:
x y
x 1.00000000 -0.02594260
y -0.02594260 1.00000000
вы можете играть с параметрами covRob, чтобы решить, как обрезать данные.
обновление: есть еще rlm (надежная линейная регрессия) в MASS пакета.
вот еще одна возможность с выбросами в плен. Используя подобную схему, как Прасад:
library(mvoutlier)
set.seed(1)
x <- rnorm(1000)
y <- rnorm(1000)
xy <- cbind(x, y)
outliers <- aq.plot(xy, alpha=0.975) #The documentation/default says alpha=0.025. I think the functions wants 0.975
cor.plot(x, y)
color.plot(xy)
dd.plot(xy)
uni.plot(xy)
в других ответах 500 застрял в конце x и y как выброс. Это может вызвать или не вызвать проблемы с памятью на вашем компьютере, поэтому я опустил его до 4, чтобы избежать этого.
x1 <- c(x, 4)
y1 <- c(y, 4)
xy1 <- cbind(x1, y1)
outliers1 <- aq.plot(xy1, alpha=0.975) #The documentation/default says alpha=0.025. I think the functions wants 0.975
cor.plot(x1, y1)
color.plot(xy1)
dd.plot(xy1)
uni.plot(xy1)
вот изображения из данных x1, y1, xy1:
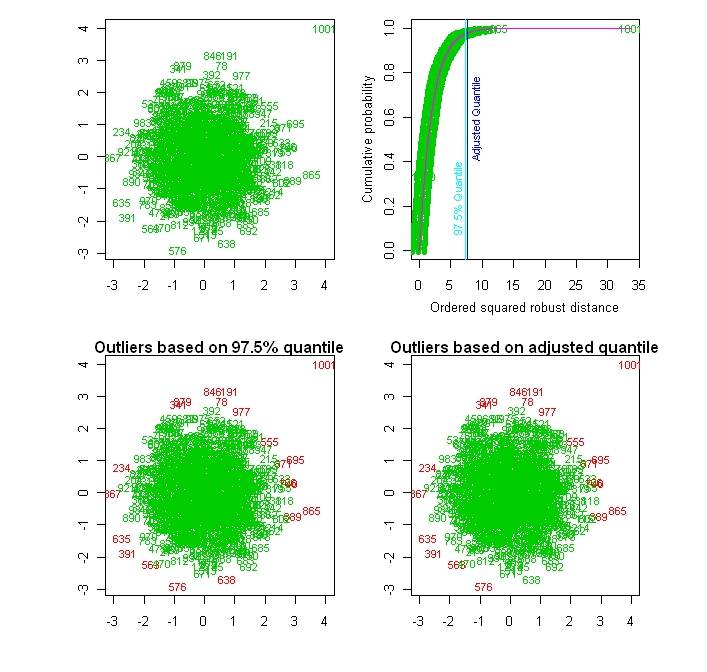
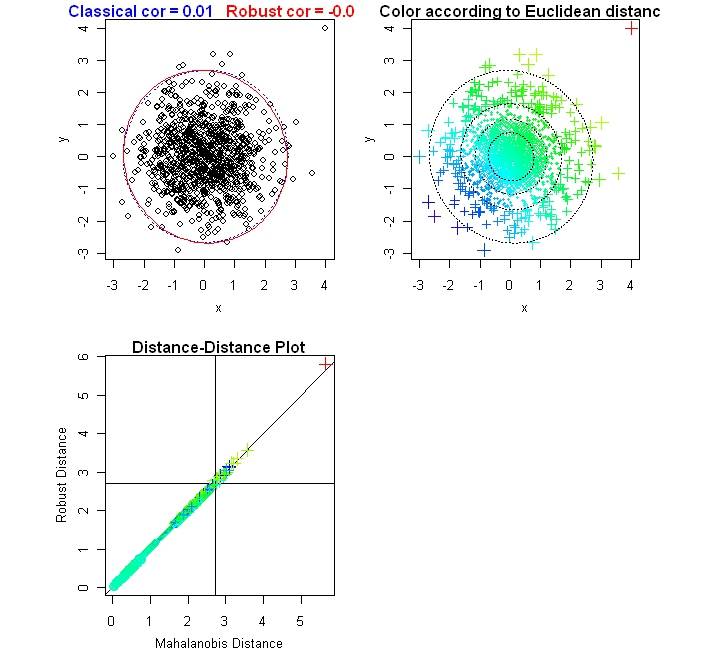
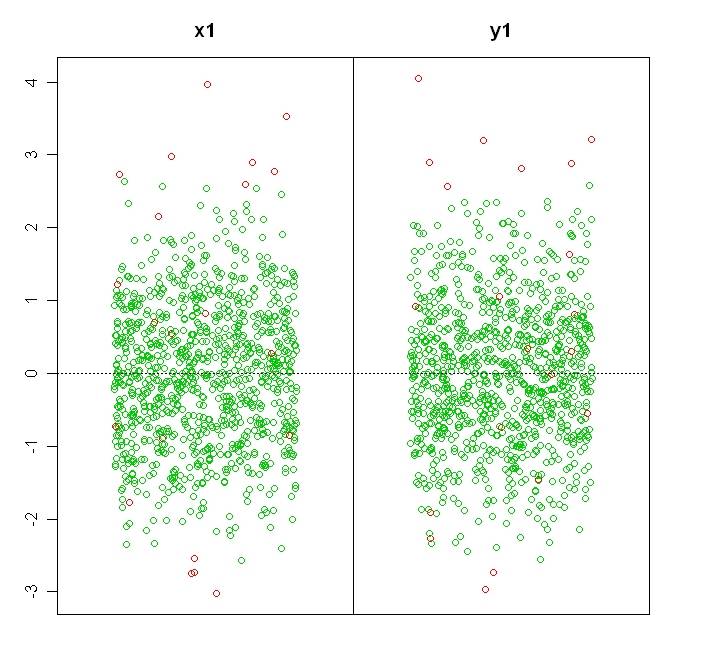
вы можете попробовать загрузить свои данные, чтобы найти самый высокий коэффициент корреляции, например:
x <- cars$dist
y <- cars$speed
percent <- 0.9 # given in the question above
n <- 1000 # number of resampling
boot.cor <- replicate(n, {tmp <- sample(round(length(x)*percent), replace=FALSE); cor(x[tmp], y[tmp])})
и после max(boot.cor). Не расстраивайтесь, если все коэффициенты корреляции будут одинаковыми:)
