Использование адаптивных размеров шага с scipy.интегрировать.ода
(краткая) документация для scipy.integrate.ode говорит, что два метода (dopri5 и dop853) имеют управление stepsize и плотный выход. Глядя на примеры и сам код, я вижу только очень простой способ выхода из интегратора. А именно, похоже, что вы просто шагаете интегратор вперед по некоторому фиксированному dt, получаете значение(ы) функции в это время и повторяете.
моя проблема имеет довольно переменные временные рамки, поэтому я хотел бы просто получить значения в любое время шаги, которые необходимо оценить для достижения требуемых допусков. То есть на раннем этапе все меняется медленно, поэтому временные шаги вывода могут быть большими. Но по мере того, как вещи становятся интересными, временные шаги вывода должны быть меньше. На самом деле я не хочу плотного вывода через равные промежутки времени, я просто хочу временные шаги, используемые адаптивной функцией.
EDIT: плотный выход
родственным понятием (почти противоположным) является "плотный выход", в результате чего предпринятые шаги так же велики, как stepper заботится о том, чтобы взять, но значения функции интерполируются (обычно с точностью, сопоставимой с точностью stepper) на все, что вы хотите. Фортран базовых scipy.integrate.ode по-видимому, способен на это, но ode не имеет интерфейса. odeint, С другой стороны, основан на другом коде и, очевидно, делает плотный вывод. (Вы можете выводить каждый раз, когда вызывается ваша правая сторона, чтобы увидеть, когда это произойдет, и увидеть, что это не имеет ничего общего с выводом раз.)
таким образом, я все еще могу воспользоваться адаптивностью, пока я могу решить, какие шаги времени выхода я хочу раньше времени. К сожалению, для моей любимой системы я даже не знаю, каковы приблизительные временные рамки как функции времени, пока я не запустил интеграцию. Поэтому мне придется объединить идею сделать один шаг интегратора с этим понятием плотного вывода.
EDIT 2: плотный выход снова
по-видимому, scipy 1.0.0 представил поддержку для плотного выхода через новый интерфейс. В частности, они рекомендуют отойти от scipy.integrate.odeint и к scipy.integrate.solve_ivp, который в качестве ключевого слова dense_output. Если установлено значение True, возвращаемый объект имеет атрибут sol который вы можете вызвать с массивом времен, который затем возвращает значения интегрированных функций в это время. Это все еще не решает проблему для этого вопроса, но это полезно во многих случаях.
5 ответов
С SciPy 0.13.0,
промежуточные результаты
dopriсемейство решателей ODE может теперь доступ кsoloutфункции обратного вызова.
import numpy as np
from scipy.integrate import ode
import matplotlib.pyplot as plt
def logistic(t, y, r):
return r * y * (1.0 - y)
r = .01
t0 = 0
y0 = 1e-5
t1 = 5000.0
backend = 'dopri5'
# backend = 'dop853'
solver = ode(logistic).set_integrator(backend)
sol = []
def solout(t, y):
sol.append([t, *y])
solver.set_solout(solout)
solver.set_initial_value(y0, t0).set_f_params(r)
solver.integrate(t1)
sol = np.array(sol)
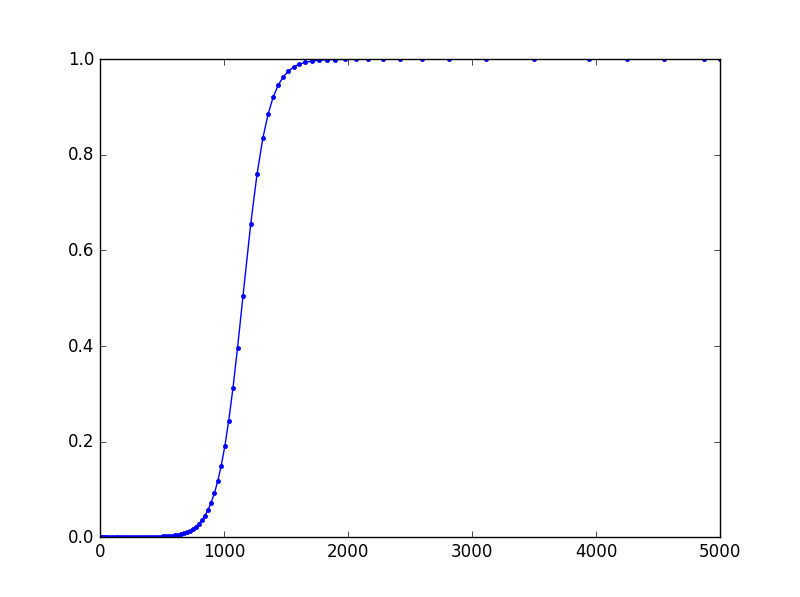
plt.plot(sol[:,0], sol[:,1], 'b.-')
plt.show()
результат, кажется, немного отличается от Tim D, хотя они оба используют один и тот же бэкэнд. Я подозреваю, что это связано с свойством FSAL dopri5. В подходе Тима я думаю, что результат k7 от седьмого этап отбрасывается, поэтому k1 рассчитывается заново.
Примечание: есть известный ошибка с set_solout не работает, если вы установите его после установки начальных значений. Это было зафиксировано как SciPy 0.17.0.
Я смотрю на это, чтобы попытаться получить тот же результат. Оказывается, вы можете использовать хак, чтобы получить пошаговые результаты, установив nsteps=1 в экземпляре ode. Он будет генерировать UserWarning на каждом шагу (это может быть поймано и подавлено).
import numpy as np
from scipy.integrate import ode
import matplotlib.pyplot as plt
import warnings
def logistic(t, y, r):
return r * y * (1.0 - y)
r = .01
t0 = 0
y0 = 1e-5
t1 = 5000.0
#backend = 'vode'
backend = 'dopri5'
#backend = 'dop853'
solver = ode(logistic).set_integrator(backend, nsteps=1)
solver.set_initial_value(y0, t0).set_f_params(r)
# suppress Fortran-printed warning
solver._integrator.iwork[2] = -1
sol = []
warnings.filterwarnings("ignore", category=UserWarning)
while solver.t < t1:
solver.integrate(t1, step=True)
sol.append([solver.t, solver.y])
warnings.resetwarnings()
sol = np.array(sol)
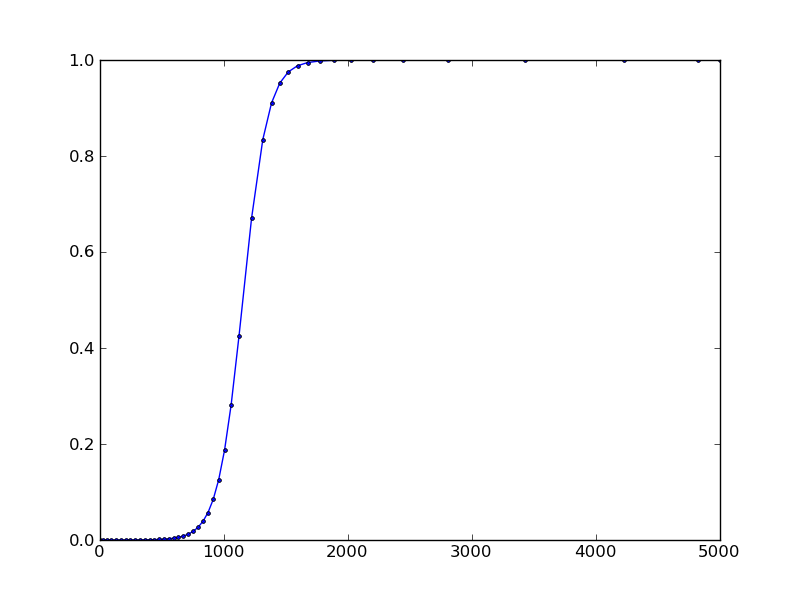
plt.plot(sol[:,0], sol[:,1], 'b.-')
plt.show()
результат:
на integrate метод принимает аргумент типа boolean step это говорит методу о возврате одного внутреннего шага. Однако, похоже, что решатели "dopri5" и "dop853" не поддерживают его.
следующий код показывает, как вы можете получить внутренние шаги, предпринятые решателем, когда используется решатель "vode":
import numpy as np
from scipy.integrate import ode
import matplotlib.pyplot as plt
def logistic(t, y, r):
return r * y * (1.0 - y)
r = .01
t0 = 0
y0 = 1e-5
t1 = 5000.0
backend = 'vode'
#backend = 'dopri5'
#backend = 'dop853'
solver = ode(logistic).set_integrator(backend)
solver.set_initial_value(y0, t0).set_f_params(r)
sol = []
while solver.successful() and solver.t < t1:
solver.integrate(t1, step=True)
sol.append([solver.t, solver.y])
sol = np.array(sol)
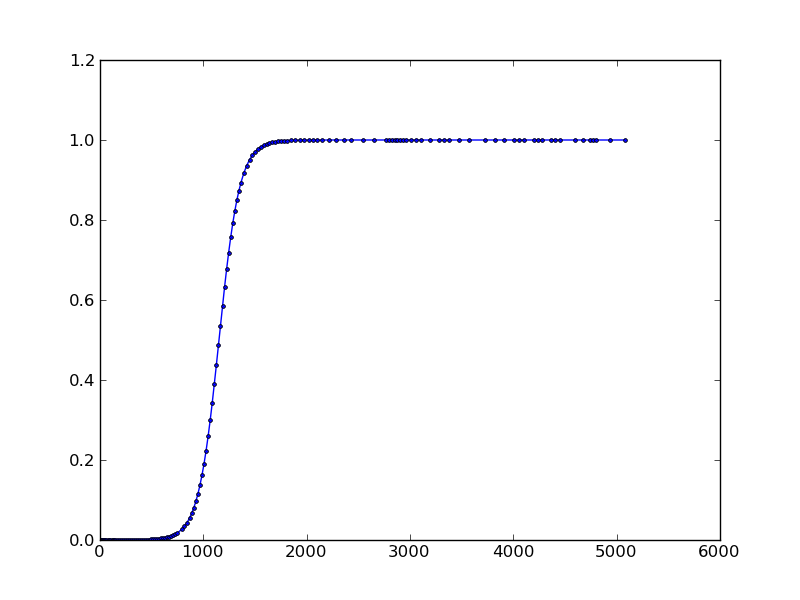
plt.plot(sol[:,0], sol[:,1], 'b.-')
plt.show()
результат:
FYI, хотя ответ уже принят, я должен указать для исторической записи, что плотный выход и произвольная выборка из в любом месте вдоль вычисленной траектории изначально поддерживается в PyDSTool. Это также включает запись всех адаптивно определенных временных шагов, используемых внутри решателя. Это взаимодействует с обоими dopri853 и radau5 и автоматически генерирует код C, необходимый для взаимодействия с ними, а не полагаясь на (гораздо медленнее) обратные вызовы функции python для определения правой стороны. Ни одна из этих функций изначально или оперативно предоставляется в любом другом Python-ориентированный решатель, насколько мне известно.
вот еще один вариант, который также должен работать с dopri5 и dop853. В принципе, решатель вызовет logistic() функция так часто, как это необходимо для расчета промежуточных значений, так что мы храним результаты:
import numpy as np
from scipy.integrate import ode
import matplotlib.pyplot as plt
sol = []
def logistic(t, y, r):
sol.append([t, y])
return r * y * (1.0 - y)
r = .01
t0 = 0
y0 = 1e-5
t1 = 5000.0
# Maximum number of steps that the integrator is allowed
# to do along the whole interval [t0, t1].
N = 10000
#backend = 'vode'
backend = 'dopri5'
#backend = 'dop853'
solver = ode(logistic).set_integrator(backend, nsteps=N)
solver.set_initial_value(y0, t0).set_f_params(r)
# Single call to solver.integrate()
solver.integrate(t1)
sol = np.array(sol)
plt.plot(sol[:,0], sol[:,1], 'b.-')
plt.show()