Использование BFS для взвешенных графов
я пересматривал алгоритмы кратчайшего пути с одним источником, и в видео учитель упоминает, что BFS / DFS не может использоваться непосредственно для поиска кратчайших путей на взвешенного графа (Я думаю, все это уже знают) и сказал, чтобы выяснить причину самостоятельно.
Мне было интересно узнать точную причину / объяснение, почему его нельзя использовать для взвешенных графиков. Это из-за веса ребер или что-то еще ? Может кто-нибудь объясните мне, как я чувствую себя немного запутался.
PS: я прошел этой сомнение и этой вопрос.
2 ответов
рассмотрим такой график:
A---(3)-----B
| |
\-(1)-C--(1)/
самый короткий путь от A до B через C (с общим весом 2). Нормальный BFS будет проходить путь непосредственно от A до B, отмечая B, как видно, и A до C, отмечая C, как видно.
на следующем этапе, распространяясь от C, B уже отмечен, как видно, поэтому путь от C до B не будет рассматриваться как потенциальный более короткий путь, и BFS скажет вам, что самый короткий путь от A до B имеет вес 3.
вы может использовать алгоритм Дейкстры вместо BFS найти кратчайший путь на взвешенном графике. Функционально алгоритм очень похож на BFS и может быть написан аналогично BFS. Единственное, что меняется-это порядок, в котором вы считаете узлов.
например, на приведенном выше графике, начиная с A, BFS будет обрабатывать A --> B, затем A --> C и останавливаться там, потому что все узлы были замечены.
С другой стороны, алгоритм Дейкстры будет действуйте следующим образом:
- рассмотрим A --> C (так как это самый низкий вес края от A)
- рассмотрим C --> B (так как это край с наименьшим весом из любого узла, которого мы достигли до сих пор, что мы еще не рассматривали)
- рассмотреть и игнорировать A --> B, так как B уже был замечен.
обратите внимание, что разница заключается просто в ордер в котором края проверены. A BFS рассмотрит все ребра от одного узла перед переходом к другим узлам, в то время как алгоритм Дейкстры всегда будет учитывать самый низкий-вес невидимый edge, из набора ребер, подключенных к все узлы, которые наблюдались до сих пор. Это звучит запутанно, но псевдокод очень прост:
create a heap or priority queue
place the starting node in the heap
dist[2...n] = {∞}
dist[1] = 0
while the heap contains items:
vertex v = top of heap
pop top of heap
for each vertex u connected to v:
if dist[u] > dist[v] + weight of v-->u:
dist[u] = dist[v] + weight of edge v-->u
place u on the heap with weight dist[u]
эта GIF из Википедии обеспечивает хорошую визуализацию того, что происходит:
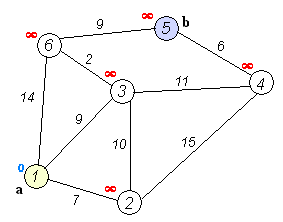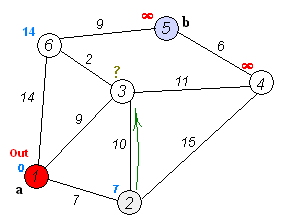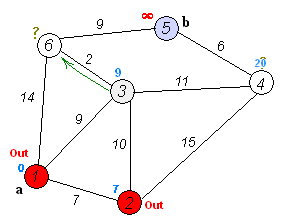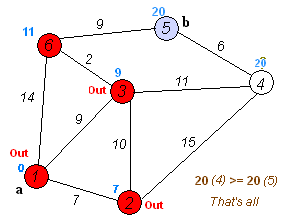
обратите внимание, что это выглядит очень похоже код ДЦ, единственное реальное различие-использование кучи, отсортированной по расстоянию до узла, вместо обычной структуры данных очереди.
хотя это правда, но вы могли бы использовать BFS/DFS в взвешенных графах с небольшим изменением графика, Если веса вашего графика являются целыми положительными числами, вы можете заменить ребро на вес n С n края с весом 1 с n-1 средние узлы. Что-то вроде этого:--8-->
A-(4)-B
будет:
A-(1)-M1-(1)-M2-(1)-M3-(1)-B
и не учитывайте эти средние узлы (например,M1,M2, M3 ) в ваших конечных результатах BFS/DFS.
эта сложность алгоритма равна O (V * M) и M-максимальный вес наших ребер, если мы знаем, что в наших конкретных графах M<log V этот алгоритм может быть рассмотрен, но в целом этот алгоритм может не иметь такой хорошей производительности.
