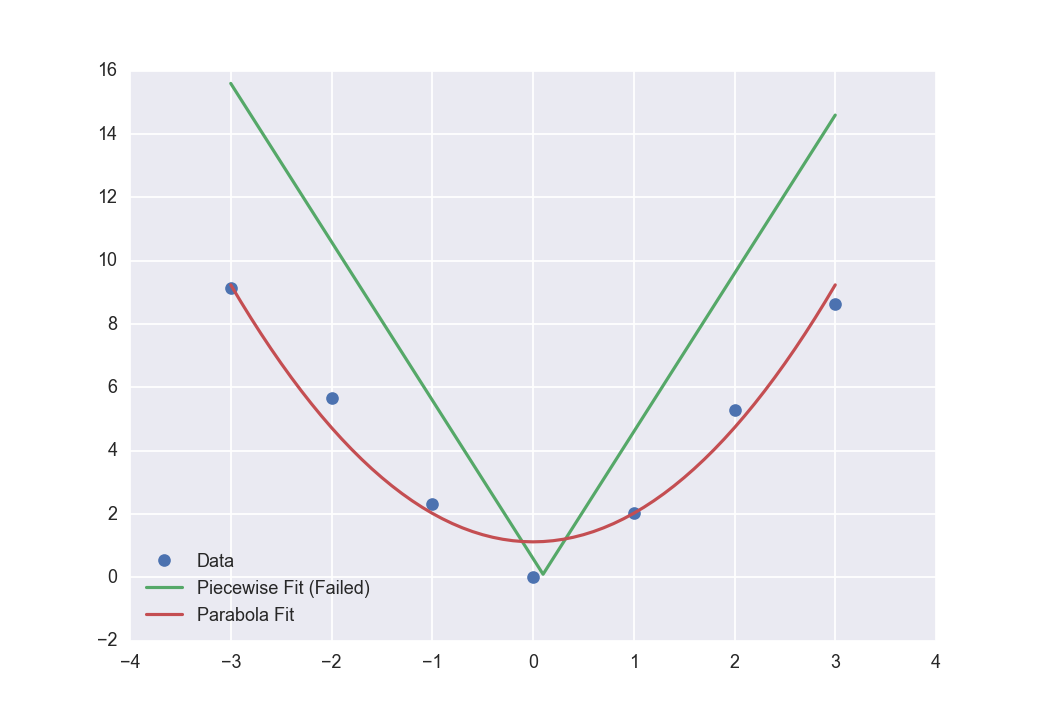
Использование кривой Scipy с кусочной функцией
Я получаю предупреждение оптимизации:
OptimizeWarning: Covariance of the parameters could not be estimated
category=OptimizeWarning)
при попытке соответствовать моей кусочной функции моим данным с помощью scipy.optimize.curve_fit. То есть никакой подгонки не происходит. Я могу легко поместить параболу в свои данные, и я предоставляю curve_fit С тем, что я чувствую, являются хорошими начальными параметрами. Полный пример кода ниже. Кто-нибудь знает, почему curve_fit может не ладить с np.piecewise? Или я делаю ошибку?
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
def piecewise_linear(x, x0, y0, k1, k2):
y = np.piecewise(x, [x < x0, x >= x0],
[lambda x:k1*x + y0-k1*x0, lambda x:k2*x + y0-k2*x0])
return y
def parabola(x, a, b):
y = a * x**2 + b
return y
x = np.array([-3, -2, -1, 0, 1, 2, 3])
y = np.array([9.15, 5.68, 2.32, 0.00, 2.05, 5.29, 8.62])
popt_piecewise, pcov = curve_fit(piecewise_linear, x, y, p0=[0.1, 0.1, -5, 5])
popt_parabola, pcov = curve_fit(parabola, x, y, p0=[1, 1])
new_x = np.linspace(x.min(), x.max(), 61)
fig, ax = plt.subplots()
ax.plot(x, y, 'o', ls='')
ax.plot(new_x, piecewise_linear(new_x, *popt_piecewise))
ax.plot(new_x, parabola(new_x, *popt_parabola))
ax.set_xlim(-4, 4)
ax.set_ylim(-2, 16)
2 ответов
это проблема с типами, вы должны изменить следующую строку, так что x дается как поплавки:
x = np.array([-3, -2, -1, 0, 1, 2, 3]).astype(np.float)
иначе piecewise_linear Уилл может в конечном итоге кастинг типов.
просто на всякий случай вы также можете сделать начальные точки плавающими здесь:
popt_piecewise, pcov = curve_fit(piecewise_linear, x, y, p0=[0.1, 0.1, -5., 5.])
для полноты я укажу, что подгонка кусочно-линейной функции не требует np.piecewise: любая такая функция может быть построена из абсолютных величин, используя кратные np.abs(x-x0) для каждого изгиба. Следующее дает хорошее соответствие данным:
def pl(x, x0, a, b, c):
y = a*np.abs(x-x0) + b*x + c
return y
popt_pl, pcov = curve_fit(pl, x, y, p0=[0, 0, 0, 0])
print(pl(x, *popt_pl))
вывод близок к исходным значениям y:
[ 8.90899998 5.828 2.74700002 -0.33399996 2.03499998 5.32
8.60500002]