изменение частоты с помощью fft и ifft, не используя целые числа
Я знаю, что могу изменить частоту целыми числами, изменив переменную shift но как я могу изменить частота использование чисел с десятичными знаками, такими как .754 или 1.2345 или 67.456. Если я изменю переменную 'shift' к нецелому, как число, как 5.1 я получаю индексы индекса ошибки должны быть либо целыми положительными числами меньше 2^31, либо logicals в строке mag2s = [mag2 (shift+1: end), нули(1, shift)];
пример кода ниже из вопроса увеличение / уменьшение частоты сигнала с помощью fft и ifft в matlab / octave работает с изменением переменной shift (но он работает только с целыми числами, мне нужно, чтобы он работал с десятичными числами также).
PS: я использую октаву 3.8.1, которая похожа на matlab, и я знаю, что могу изменить частоту, отрегулировав формулу в переменная ya но ya будет сигнал, взятый из источника звука (человеческая речь), поэтому это не будет уравнение. Уравнение просто используется, чтобы сохранить пример простым. И да, Fs велик из-за того, что используемые сигнальные файлы имеют длину около 45 секунд, поэтому я не могу использовать resample, потому что при использовании я получаю ошибку из памяти.
вот анимированный пример видео youtube о том, что я пытаюсь получить, когда я использую тестовое уравнение ya= .5 * sin (2*pi*1*t)+.2 * cos (2*pi*3*t) и то, что я пытаюсь получить, произойдет, если я изменил переменную shift от (0:0.1:5) Юту.be / pf25Gw6iS1U пожалуйста, имейте в виду, что ya будет импортированным аудиосигналом, поэтому у меня не будет уравнения для легкой настройки
clear all,clf
Fs = 2000000;% Sampling frequency
t=linspace(0,1,Fs);
%1a create signal
ya = .5*sin(2*pi*2*t);
%2a create frequency domain
ya_fft = fft(ya);
mag = abs(ya_fft);
phase = unwrap(angle(ya_fft));
ya_newifft=ifft(mag.*exp(i*phase));
% ----- changes start here ----- %
shift = 5; % shift amount
N = length(ya_fft); % number of points in the fft
mag1 = mag(2:N/2+1); % get positive freq. magnitude
phase1 = phase(2:N/2+1); % get positive freq. phases
mag2 = mag(N/2+2:end); % get negative freq. magnitude
phase2 = phase(N/2+2:end); % get negative freq. phases
% pad the positive frequency signals with 'shift' zeros on the left
% remove 'shift' components on the right
mag1s = [zeros(1,shift) , mag1(1:end-shift)];
phase1s = [zeros(1,shift) , phase1(1:end-shift)];
% pad the negative frequency signals with 'shift' zeros on the right
% remove 'shift' components on the left
mag2s = [mag2(shift+1:end), zeros(1,shift)];
phase2s = [phase2(shift+1:end), zeros(1,shift) ];
% recreate the frequency spectrum after the shift
% DC +ve freq. -ve freq.
magS = [mag(1) , mag1s , mag2s];
phaseS = [phase(1) , phase1s , phase2s];
x = magS.*cos(phaseS); % change from polar to rectangular
y = magS.*sin(phaseS);
yafft2 = x + i*y; % store signal as complex numbers
yaifft2 = real(ifft(yafft2)); % take inverse fft
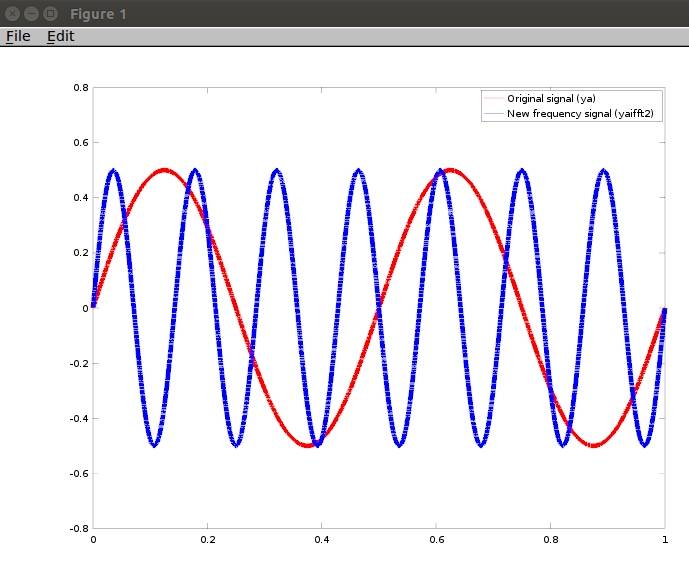
plot(t,ya,'-r',t,yaifft2,'-b'); % time signal with increased frequency
legend('Original signal (ya) ','New frequency signal (yaifft2) ')
3 ответов
хорошо, поэтому вопрос, как я понимаю, это "как я могу сдвинуть свой сигнал на определенную частоту?"
сначала давайте определим Fs, который является нашей частотой дискретизации (т. е. образцы в секунду). Мы собираем сигнал длиной N выборок. Тогда изменение частоты между образцами в области Фурье-Fs / N. поэтому, принимая ваш пример кода Fs-2,000,000 и N-2,000,000, поэтому пространство между каждым образцом составляет 1 Гц, а сдвиг вашего сигнала 5 образцов сдвигает его на 5 Гц.
теперь скажите, что мы хотим вместо этого сдвинуть наш сигнал на 5,25 Гц. Ну, если бы наш сигнал был 8,000,000 образцов, то расстояние было бы Fs/N = 0,25 Гц, и мы бы сдвинули наш сигнал 11 образцов. Итак,как мы получаем сигнал 8,000,000 sample из сигнала 2,000,000 sample? Просто zero pad это! буквально дописать нули до 8,000,000 образцы долго. Почему это работает? Потому что вы, по сути, умножаете свой сигнал на прямоугольное окно, которое эквивалентно свертке функции sinc в частотной области. Это важный момент. Добавляя нули, вы интерполируете в частотной области (у вас больше нет частотной информации о сигнале, который вы просто интерполируете между предыдущими точками DTFT).
мы можем сделать это до любого разрешения, которое вы хотите, но в конечном итоге вам придется иметь дело с тем, что числа в цифровых системах не являются непрерывными, поэтому я рекомендую просто выбрать приемлемый допуск. Допустим, мы хотим быть в пределах 0,01 от желаемой частоты.
Итак, давайте перейдем к фактическому коду. К счастью, большинство из них не меняется.
clear all,clf
Fs = 44100; % lets pick actual audio sampling rate
tolerance = 0.01; % our frequency bin tolerance
minSignalLen = Fs / tolerance; %minimum number of samples for our tolerance
%your code does not like odd length signals so lets make sure we have an
%even signal length
if(mod(minSignalLen,2) ~=0 )
minSignalLen = minSignalLen + 1;
end
t=linspace(0,1,Fs); %our input signal is 1s long
%1a create 2Hz signal
ya = .5*sin(2*pi*2*t);
if (length(ya) < minSignalLen)
ya = [ya, zeros(1, minSignalLen - length(ya))];
end
df = Fs / length(ya); %actual frequency domain spacing;
targetFreqShift = 2.32; %lets shift it 2.32Hz
nSamplesShift = round(targetFreqShift / df);
%2a create frequency domain
ya_fft = fft(ya);
mag = abs(ya_fft);
phase = unwrap(angle(ya_fft));
ya_newifft=ifft(mag.*exp(i*phase));
% ----- changes start here ----- %
shift = nSamplesShift; % shift amount
N = length(ya_fft); % number of points in the fft
mag1 = mag(2:N/2+1); % get positive freq. magnitude
phase1 = phase(2:N/2+1); % get positive freq. phases
mag2 = mag(N/2+2:end); % get negative freq. magnitude
phase2 = phase(N/2+2:end); % get negative freq. phases
% pad the positive frequency signals with 'shift' zeros on the left
% remove 'shift' components on the right
mag1s = [zeros(1,shift) , mag1(1:end-shift)];
phase1s = [zeros(1,shift) , phase1(1:end-shift)];
% pad the negative frequency signals with 'shift' zeros on the right
% remove 'shift' components on the left
mag2s = [mag2(shift+1:end), zeros(1,shift)];
phase2s = [phase2(shift+1:end), zeros(1,shift) ];
% recreate the frequency spectrum after the shift
% DC +ve freq. -ve freq.
magS = [mag(1) , mag1s , mag2s];
phaseS = [phase(1) , phase1s , phase2s];
x = magS.*cos(phaseS); % change from polar to rectangular
y = magS.*sin(phaseS);
yafft2 = x + i*y; % store signal as complex numbers
yaifft2 = real(ifft(yafft2)); % take inverse fft
%pull out the original 1s of signal
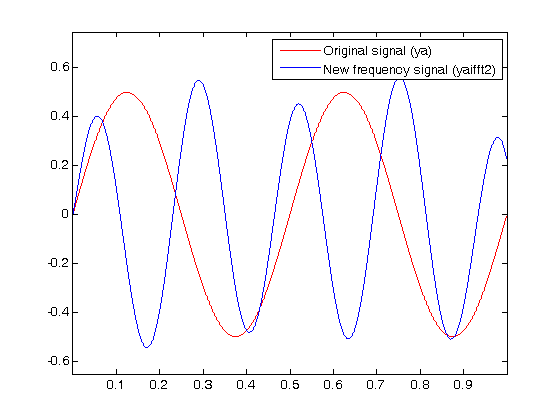
plot(t,ya(1:length(t)),'-r',t,yaifft2(1:length(t)),'-b');
legend('Original signal (ya) ','New frequency signal (yaifft2) ')
окончательный сигнал немного над 4Hz которое чего мы предпологаем. Существует некоторое искажение, видимое из интерполяции, но это должно быть сведено к минимуму с более длинным сигналом с представлением частотной области.
теперь, когда я прошел через все это, вам может быть интересно, есть ли более простой способ. К счастью для нас, Есть. Мы можем воспользоваться свойствами преобразования Гильберта и преобразования Фурье для достижения сдвига частоты, не беспокоясь о Fs или уровнях допуска или интервале между ячейками. А именно, мы знаем, что временной сдвиг приводит к фазовому сдвигу в области Фурье. Ну, время и частота являются дуалами, поэтому сдвиг частоты приводит к сложному экспоненциальному умножению во временной области. Мы не хотим просто делать массовый сдвиг всех частот, потому что это разрушит нашу симметрию в Фурье пространство, ведущее к сложным временным рядам. Поэтому мы используем преобразование Гильберта, чтобы получить аналитический сигнал, состоящий только из положительных частот, сдвинуть его, а затем реконструировать наш временной ряд, предполагая симметричное представление Фурье.
Fs = 44100;
t=linspace(0,1,Fs);
FShift = 2.3 %shift our frequency up by 2.3Hz
%1a create signal
ya = .5*sin(2*pi*2*t);
yaHil = hilbert(ya); %get the hilbert transform
yaShiftedHil = yaHil.*exp(1i*2*pi*FShift*t);
yaShifted = real(yaShiftedHil);
figure
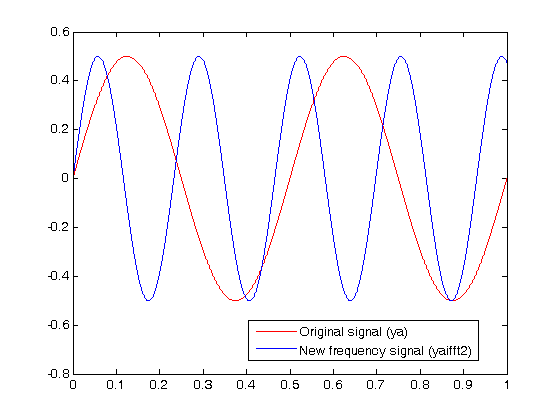
plot(t,ya,'-r',t,yaShifted,'-b')
legend('Original signal (ya) ','New frequency signal (yaifft2) ')
вы можете сделать это с помощью частичной задержки фильтра.
во-первых, позволяет сделать код работоспособным, позволяя Matlab обрабатывать сопряженную симметрию БПФ. Просто сделайте mag1 и phase1 перейти к концу . . .
mag1 = mag(2:end);
phase1 = phase(2:end);
избавиться mag2s и phase2s полностью. Это упрощает строки 37 и 38 . .
magS = [mag(1) , mag1s ];
phaseS = [phase(1) , phase1s ];
использовать на ifft чтобы заставить Matlb обрабатывать симметрию для вас. Затем вы можете отбросить forced real, тоже.
yaifft2 = ifft(yafft2, 'symmetric'); % take inverse fft
С этим очищено, теперь мы можем думать о задержке как фильтр, например
% ----- changes start here ----- %
shift = 5;
shift_b = [zeros(1, shift) 1]; % shift amount
shift_a = 1;
который может быть применен как таковой . . .
mag1s = filter(shift_b, shift_a, mag1);
phase1s = filter(shift_b, shift_a, phase1);
в этом мышлении мы можем использовать фильтр allpass, чтобы сделать очень простой фильтр дробной задержки
код выше дает "M образцов задержки" часть схемы. Затем вы можете добавить фракцию, используя второй каскадный фильтр allpass . .
shift = 5.5;
Nw = floor(shift);
shift_b = [zeros(1, Nw) 1];
shift_a = 1;
Nf = mod(shift,1);
alpha = -(Nf-1)/(Nf+1);
fract_b = [alpha 1];
fract_a = [1 alpha];
%// now filter as a cascade . . .
mag1s = filter(shift_b, shift_a, mag1);
mag1s = filter(fract_b, fract_a, mag1s);
интерполяция с ограниченной полосой с использованием ядра интерполяции windowed-Sinc может использоваться для изменения частоты дискретизации по произвольным соотношениям. Изменение частоты дискретизации изменяет частотное содержание сигнала относительно частоты дискретизации на обратное отношение.