Как генерировать распределения, заданные, средние, SD, перекос и эксцесс в R?

можно ли генерировать распределения в R, для которых известны среднее, SD, перекос и эксцесс? Пока кажется, что лучшим путем было бы создать случайные числа и преобразовать их соответственно. Если есть пакет, предназначенный для генерации конкретных распределений, которые могут быть адаптированы, я еще не нашел его. Спасибо

33
frequency-distribution r skew statistics

6 ответов

в пакете SuppDists есть дистрибутив Johnson. Джонсон даст вам распределение, которое соответствует либо моментам, либо квантилям. Другие комментарии верны, что 4 moments не делает дистрибутив. Но Джонсон обязательно попытается.

вот пример подгонки Johnson к некоторым образцам данных:

require(SuppDists)

## make a weird dist with Kurtosis and Skew
a <- rnorm( 5000, 0, 2 )
b <- rnorm( 1000, -2, 4 )
c <- rnorm( 3000,  4, 4 )
babyGotKurtosis <- c( a, b, c )
hist( babyGotKurtosis , freq=FALSE)

## Fit a Johnson distribution to the data
## TODO: Insert Johnson joke here
parms<-JohnsonFit(babyGotKurtosis, moment="find")

## Print out the parameters 
sJohnson(parms)

## add the Johnson function to the histogram
plot(function(x)dJohnson(x,parms), -20, 20, add=TRUE, col="red")

финальный сюжет выглядит так:

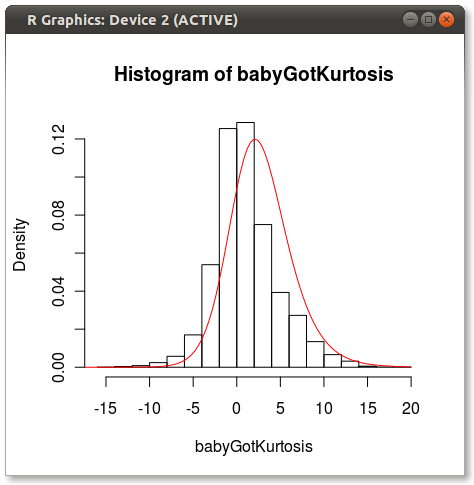
enter image description here

вы можете увидеть немного проблемы, которую другие указывают о том, как 4 моменты не полностью захватывают распределение.

удачи!

редактировать Как отметил Хэдли в комментариях, The Johnson fit смотрит прочь. Я сделал быстрый тест и поместил распределение Джонсона, используя moment="quant" который соответствует распределению Джонсона, используя 5 квантилей вместо 4 моментов. Результаты выглядят намного лучше:

parms<-JohnsonFit(babyGotKurtosis, moment="quant")
plot(function(x)dJohnson(x,parms), -20, 20, add=TRUE, col="red")

который производит следующее:

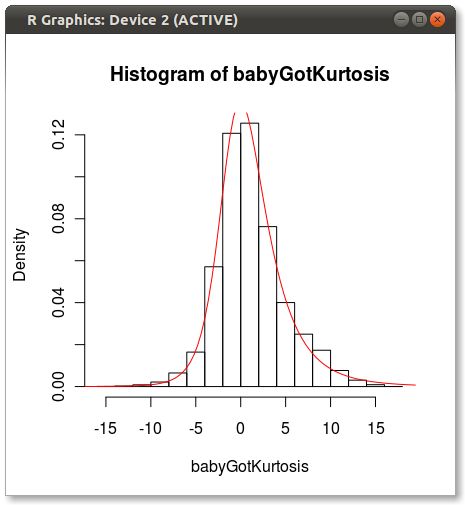
enter image description here

У кого-нибудь есть идеи, почему Джонсон кажется предвзято, когда подходят моменты?

32

Это интересный вопрос, который на самом деле не есть хорошее решение. Я предполагаю, что, хотя вы не знаете других моментов, у вас есть представление о том, как должно выглядеть распределение. Например, это unimodal.

Существует несколько различных способов решения этой проблемы:

  1. предположим базовое распределение и совпадение моментов. Есть много стандартными пакетами R для этого. Одним из недостатков является то, что многомерное обобщение может быть неясно.

  2. Saddlepoint приближений. В этой статье:

    Гиллеспи, К. С. и Реншоу, Е. улучшенная аппроксимация saddlepoint. Математическая Биология 2007,.

    мы смотрим на восстановление pdf / pmf, когда дается только первые несколько минут. Мы обнаружили, что этот подход работает, когда асимметрия не слишком велика.

  3. Лагерра разложения:

    Mustapha, H. and Dimitrakopoulosa, Р. обобщенные разложения Лагерра многомерных плотностей вероятностей с моментами. компьютеры и математика с приложениями 2010,.

    результаты в этой статье кажутся более многообещающими, но я их не закодировал.

12

этот вопрос был задан более 3 лет назад, поэтому я надеюсь, что мой ответ не приходит слишком поздно.

здесь is способ уникальной идентификации распределения при знании некоторых моментов. Таким образом, метод Максимальной Энтропии. Распределение, которое является результатом этого метода, является распределением, которое максимизирует ваше незнание о структуре распределения,учитывая, что вы знаете. Любое другое распределение, которое также имеет моменты, которые вы указали, но не являются распределением MaxEnt, неявно предполагают большую структуру, чем то, что вы вводите. Функционал для максимизации-информационная энтропия Шеннона, $S[p(x)] = - \int p(x)log p (x) dx$. Зная среднее, sd, асимметрию и эксцесс, переводим как ограничения на первый, второй, третий и четвертый моменты распределения соответственно.

проблема заключается в том, чтобы максимизировать S С учетом ограничений: 1) $\int x p (x) dx = " первый момент$", 2) $\int x^2 p (x) dx = "второй момент"$, 3) ... и так далее

рекомендую книгу " Harte, J., максимальная Энтропия и экология: теория изобилия, распределения и энергетика (Oxford University Press, New York, 2011)."

вот ссылка, которая пытается реализовать это в R: https://stats.stackexchange.com/questions/21173/max-entropy-solver-in-r

7

Я согласен, что вам нужна оценка плотности для репликации любого распределения. Однако, если у вас есть сотни переменных, как это типично для моделирования Монте-Карло, вам нужно будет найти компромисс.

один из предложенных подходов заключается в следующем:

  1. используйте преобразование Флейшмана, чтобы получить коэффициент для данного перекоса и эксцесса. Флейшман берет перекос и эксцесс и дает вам коэффициенты
  2. генерировать N нормальных переменных (среднее = 0, std = 1)
  3. преобразуйте данные в (2) с коэффициентами Флейшмана, чтобы преобразовать нормальные данные в заданный перекос и эксцесс
  4. на этом шаге используйте данные из Шага (3) и преобразуйте их в желаемое среднее и стандартное отклонение (std), используя new_data = желаемое среднее + (данные из Шага 3)* желаемое std

полученные данные из шага 4 будут иметь желаемое среднее значение, std, асимметрию и эксцесс.

предостережения:

  1. Флейшман не будет работать для всех комбинаций асимметрии и Куртуа
  2. выше шаги предполагают некоррелированные переменные. Если вы хотите создать коррелированные данные, вам понадобится шаг до преобразования Флейшмана
3

эти параметры фактически не полностью определяют распределение. Для этого нужна плотность или функция распределения.

2

Как писали @David и @Carl выше, существует несколько пакетов, предназначенных для генерации различных дистрибутивов, см., например,представление задачи распределения вероятностей на CRAN.

Если вас интересует теория (Как нарисовать выборку чисел, соответствующих определенному распределению с заданными параметрами), то просто найдите соответствующие формулы, например, см. гамма-распределение на Wiki, и составляют простую систему качества с параметры для вычисления масштаба и формы.

см. конкретный пример здесь, где вычисляются альфа-и бета-параметры требуемого бета-распределения на основе среднего и стандартного отклонения.

0