Как использовать фильтр Калмана в Python для данных о местоположении?

TL; DR, см. код и изображение внизу.

я думаю, что фильтр Калмана может работать довольно хорошо в вашем приложении, но для этого потребуется немного больше думать о динамике/физике воздушного змея.

я настоятельно рекомендую читать этот сайт. У меня нет связи или знаний об авторе, но я потратил около дня, пытаясь разобраться в фильтрах Калмана, и эта страница действительно заставила ее щелкнуть для мне.

кратко; для системы, которая является линейной и которая имеет известную динамику (т. е. если вы знаете состояние и входные данные, вы можете предсказать будущее состояние), она обеспечивает оптимальный способ объединения того, что вы знаете о системе, чтобы оценить ее истинное состояние. Умный бит (о котором заботится вся матричная алгебра, которую вы видите на страницах, описывающих его) - это то, как он оптимально сочетает две части информации, которые у вас есть:

1. измерения (которые при условии "измерения шума", т. е. датчики не совершенны)

2. динамика (т. е. как вы считаете, что состояния развиваются при условии ввода, которые подвержены "процессу шума", что является просто способом сказать, что ваша модель не соответствует реальности идеально).

вы указываете, насколько вы уверены в каждом из них (через матрицы ко-отклонений R и Q соответственно), а Калмана Приобрести определяет насколько вы должны верить своей модели (т. е. вашей текущей оценке вашего состояния) и насколько вы должны верить своим измерениям.

без дальнейших церемоний давайте построим простую модель кайта. Ниже я предлагаю очень простую возможную модель. Возможно,вы знаете больше о динамике змея, поэтому можете создать лучший.

давайте рассматривать кайт как частицу (очевидно, упрощение, настоящий кайт-это расширенное тело, поэтому имеет ориентацию в 3 dimensions), который имеет четыре состояния, которые для удобства можно записать в вектор состояния:

x = [x, x_dot, y, y_dot],

где x и y-положения, а DOT-скорости в каждом из этих направлений. Из вашего вопроса я предполагаю, что есть два (потенциально шумных) измерения, которые мы можем записать в вектор измерения:

z = [x, y],

мы можем записать-вниз измерение матрица (H обсуждали здесь и observation_matrices на pykalman библиотека):

z = Hx =>H = [[1, 0, 0, 0], [0, 0, 1, 0]]

затем нам нужно описать динамику системы. Здесь я предположу, что никакие внешние силы не действуют, и что нет демпфирования движения воздушного змея (с большим знанием вы можете быть в состоянии сделать лучше, это эффективно относится к внешним силам и демпфированию как неизвестный/нарушение unmodeled).

в этом случае динамика для каждого из наших состояний в текущей выборке " k "как функция состояний в предыдущих выборках" k-1 " задается как:

x(k) = x(k-1) + dt*x_dot (k-1)

x_dot(k) = x_dot (k-1)

y(k) = y(k-1) + dt*y_dot (k-1)

y_dot(k) = y_dot (k-1)

где " dt " -это временной шаг. Мы предполагаем, что положение (x, y) обновляется на основе текущего положения и скорости, и скорость остается неизменной. Учитывая, что никакие единицы не заданы, мы можем просто сказать, что единицы скорости таковы, что мы можем опустить "dt" из приведенных выше уравнений, т. е. в единицах position_units/sample_interval (я предполагаю, что ваши измеренные образцы находятся на постоянном интервале). Мы можем суммировать эти четыре уравнения в матрицу динамики (F здесь обсуждается, и transition_matrices на pykalman библиотека):

x(k)= Fx(k-1)=>F = [[1, 1, 0, 0], [0, 1, 0, 0], [0, 0, 1, 1], [0, 0, 0, 1]].

теперь мы можем использовать фильтр Калмана в python. Изменен код:

from pykalman import KalmanFilter
import numpy as np
import matplotlib.pyplot as plt
import time

measurements = np.asarray([(399,293),(403,299),(409,308),(416,315),(418,318),(420,323),(429,326),(423,328),(429,334),(431,337),(433,342),(434,352),(434,349),(433,350),(431,350),(430,349),(428,347),(427,345),(425,341),(429,338),(431,328),(410,313),(406,306),(402,299),(397,291),(391,294),(376,270),(372,272),(351,248),(336,244),(327,236),(307,220)])

initial_state_mean = [measurements[0, 0],
                      0,
                      measurements[0, 1],
                      0]

transition_matrix = [[1, 1, 0, 0],
                     [0, 1, 0, 0],
                     [0, 0, 1, 1],
                     [0, 0, 0, 1]]

observation_matrix = [[1, 0, 0, 0],
                      [0, 0, 1, 0]]

kf1 = KalmanFilter(transition_matrices = transition_matrix,
                  observation_matrices = observation_matrix,
                  initial_state_mean = initial_state_mean)

kf1 = kf1.em(measurements, n_iter=5)
(smoothed_state_means, smoothed_state_covariances) = kf1.smooth(measurements)

plt.figure(1)
times = range(measurements.shape[0])
plt.plot(times, measurements[:, 0], 'bo',
         times, measurements[:, 1], 'ro',
         times, smoothed_state_means[:, 0], 'b--',
         times, smoothed_state_means[:, 2], 'r--',)
plt.show()

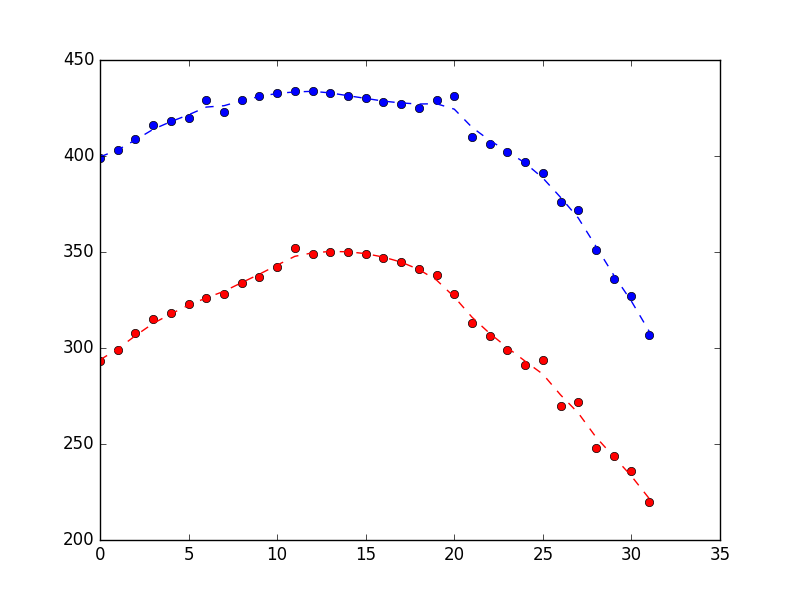
который произвел следующее, показывая, что он выполняет разумную работу по отклонению шума (синий-это позиция x, красный-позиция y, а ось x-просто номер образца).

Предположим, вы смотрите на сюжет выше и думаете, что он выглядит слишком ухабистым. Как можно исправить это? Как обсуждалось выше, фильтр Калмана действует на две части информации:

1. измерения (в данном случае двух наших состояний, x и y)
2. динамика системы (и текущая оценка состояния)

динамика, захваченная в модели выше, очень проста. Буквально они говорят, что позиции будут обновляться текущими скоростями (очевидным, физически разумным способом), и что скорости остаются постоянными (это явно не физически верно,но захватывает нашу интуицию, что скорости должны меняться медленно).

если мы думаем, что оценочное состояние должно быть более плавным, один из способов достичь этого-сказать, что у нас меньше уверенности в наших измерениях, чем в нашей динамике (т. е. у нас выше observation_covariance, по отношению к нашему state_covariance).

начиная с конца кода выше, исправить observation covariance до 10x значение, оцененное ранее, установка em_vars как показано во избежание переоценки ковариация наблюдения (см. здесь)

kf2 = KalmanFilter(transition_matrices = transition_matrix,
                  observation_matrices = observation_matrix,
                  initial_state_mean = initial_state_mean,
                  observation_covariance = 10*kf1.observation_covariance,
                  em_vars=['transition_covariance', 'initial_state_covariance'])

kf2 = kf2.em(measurements, n_iter=5)
(smoothed_state_means, smoothed_state_covariances)  = kf2.smooth(measurements)

plt.figure(2)
times = range(measurements.shape[0])
plt.plot(times, measurements[:, 0], 'bo',
         times, measurements[:, 1], 'ro',
         times, smoothed_state_means[:, 0], 'b--',
         times, smoothed_state_means[:, 2], 'r--',)
plt.show()

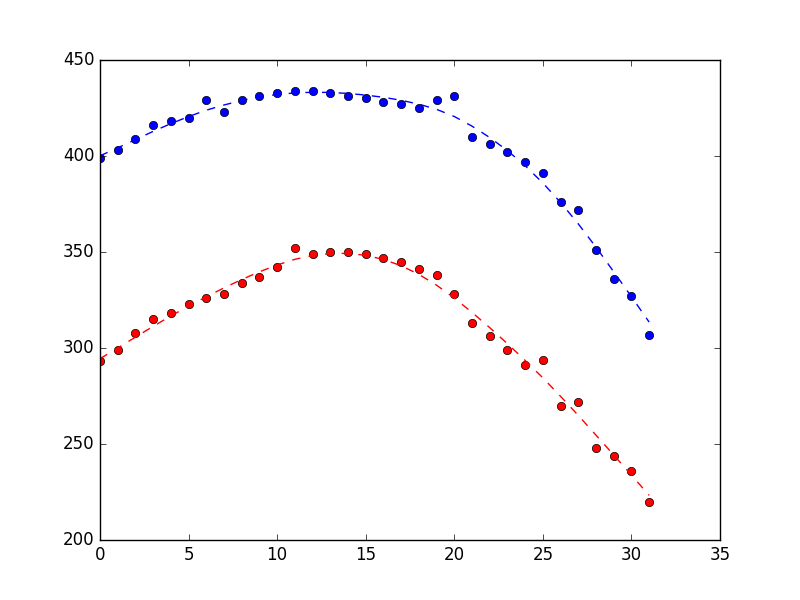
который производит график ниже (измерения как точки, оценки состояния как пунктирная линия). Разница довольно тонкая, но, надеюсь, вы видите, что она более гладкая.

наконец, если вы хотите использовать этот фильтр установлен на линии, вы можете сделать это с помощью filter_update метод. Обратите внимание, что это использует filter метод, а не smooth способ, потому что smooth метод можно только приложить к измерениям серии. Больше здесь:

time_before = time.time()
n_real_time = 3

kf3 = KalmanFilter(transition_matrices = transition_matrix,
                  observation_matrices = observation_matrix,
                  initial_state_mean = initial_state_mean,
                  observation_covariance = 10*kf1.observation_covariance,
                  em_vars=['transition_covariance', 'initial_state_covariance'])

kf3 = kf3.em(measurements[:-n_real_time, :], n_iter=5)
(filtered_state_means, filtered_state_covariances) = kf3.filter(measurements[:-n_real_time,:])

print("Time to build and train kf3: %s seconds" % (time.time() - time_before))

x_now = filtered_state_means[-1, :]
P_now = filtered_state_covariances[-1, :]
x_new = np.zeros((n_real_time, filtered_state_means.shape[1]))
i = 0

for measurement in measurements[-n_real_time:, :]:
    time_before = time.time()
    (x_now, P_now) = kf3.filter_update(filtered_state_mean = x_now,
                                       filtered_state_covariance = P_now,
                                       observation = measurement)
    print("Time to update kf3: %s seconds" % (time.time() - time_before))
    x_new[i, :] = x_now
    i = i + 1

plt.figure(3)
old_times = range(measurements.shape[0] - n_real_time)
new_times = range(measurements.shape[0]-n_real_time, measurements.shape[0])
plt.plot(times, measurements[:, 0], 'bo',
         times, measurements[:, 1], 'ro',
         old_times, filtered_state_means[:, 0], 'b--',
         old_times, filtered_state_means[:, 2], 'r--',
         new_times, x_new[:, 0], 'b-',
         new_times, x_new[:, 2], 'r-')

plt.show()

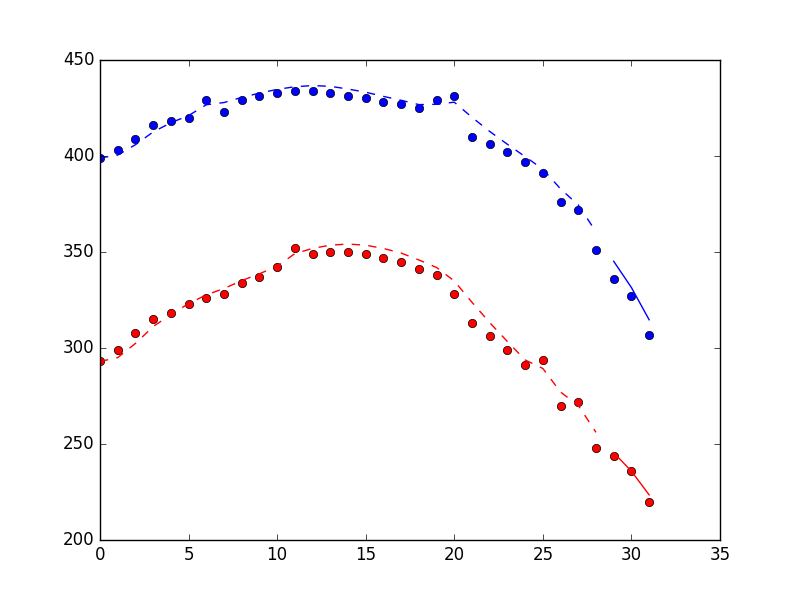
на графике ниже показана производительность метода фильтра, включая 3 точки, найденные с помощью filter_update метод. Точки-это измерения, пунктирная линия-оценки состояния для периода обучения фильтра, сплошная линия-оценки состояния для периода "on-line".

и время (по моим ноутбук.)

Time to build and train kf3: 0.0677888393402 seconds
Time to update kf3: 0.00038480758667 seconds
Time to update kf3: 0.000465154647827 seconds
Time to update kf3: 0.000463008880615 seconds