Как можно вычислить евклидово расстояние с помощью NumPy?
у меня есть две точки в 3D:
(xa, ya, za)
(xb, yb, zb)
и я хочу рассчитать расстояние:
dist = sqrt((xa-xb)^2 + (ya-yb)^2 + (za-zb)^2)
каков наилучший способ сделать это с NumPy или С Python в целом? У меня:
a = numpy.array((xa ,ya, za))
b = numpy.array((xb, yb, zb))
18 ответов
для этого есть функция в SciPy. Это называется Евклидово.
пример:
from scipy.spatial import distance
a = (1, 2, 3)
b = (4, 5, 6)
dst = distance.euclidean(a, b)
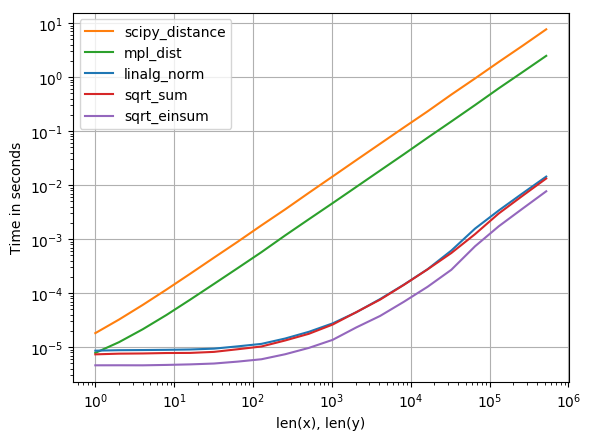
для тех, кто заинтересован в вычислении нескольких расстояний сразу, я сделал небольшое сравнение, используя perfplot (небольшой проект). Оказывается, что
a_min_b = a - b
numpy.sqrt(numpy.einsum('ij,ij->i', a_min_b, a_min_b))
вычисляет расстояния строк в a и b быстрый. На самом деле это справедливо и для одной строки!
код для воспроизведения сюжета:
import matplotlib
import numpy
import perfplot
from scipy.spatial import distance
def linalg_norm(data):
a, b = data
return numpy.linalg.norm(a-b, axis=1)
def sqrt_sum(data):
a, b = data
return numpy.sqrt(numpy.sum((a-b)**2, axis=1))
def scipy_distance(data):
a, b = data
return list(map(distance.euclidean, a, b))
def mpl_dist(data):
a, b = data
return list(map(matplotlib.mlab.dist, a, b))
def sqrt_einsum(data):
a, b = data
a_min_b = a - b
return numpy.sqrt(numpy.einsum('ij,ij->i', a_min_b, a_min_b))
perfplot.show(
setup=lambda n: numpy.random.rand(2, n, 3),
n_range=[2**k for k in range(20)],
kernels=[linalg_norm, scipy_distance, mpl_dist, sqrt_sum, sqrt_einsum],
logx=True,
logy=True,
xlabel='len(x), len(y)'
)
другой пример этот метод решения проблем:
def dist(x,y):
return numpy.sqrt(numpy.sum((x-y)**2))
a = numpy.array((xa,ya,za))
b = numpy.array((xb,yb,zb))
dist_a_b = dist(a,b)
я хочу изложить простой ответ с различными примечаниями к производительности. НП.linalg.норм сделает, возможно, больше, чем вам нужно:
dist = numpy.linalg.norm(a-b)
во-первых - эта функция предназначена для работы над списком и возврата всех значений, например, для сравнения расстояния от pA к множеству точек sP:
sP = set(points)
pA = point
distances = np.linalg.norm(sP - pA, ord=2, axis=1.) # 'distances' is a list
запомнить несколько вещей:
- вызовы функций Python дороги.
- [обычный] Python не кэширует имя поиски.
так
def distance(pointA, pointB):
dist = np.linalg.norm(pointA - pointB)
return dist
не так невинно, как кажется.
>>> dis.dis(distance)
2 0 LOAD_GLOBAL 0 (np)
2 LOAD_ATTR 1 (linalg)
4 LOAD_ATTR 2 (norm)
6 LOAD_FAST 0 (pointA)
8 LOAD_FAST 1 (pointB)
10 BINARY_SUBTRACT
12 CALL_FUNCTION 1
14 STORE_FAST 2 (dist)
3 16 LOAD_FAST 2 (dist)
18 RETURN_VALUE
во-первых-каждый раз, когда мы вызываем его, мы должны сделать глобальный поиск для "np", поиск области для" linalg "и поиск области для" нормы", а накладные расходы просто вызов функция может приравниваться к десяткам инструкций python.
наконец, мы потратили две операции на то, чтобы сохранить результат и перезагрузить его для возвращаться...
первый проход при улучшении: сделайте поиск быстрее, пропустите магазин
def distance(pointA, pointB, _norm=np.linalg.norm):
return _norm(pointA - pointB)
мы получаем гораздо более обтекаемый:
>>> dis.dis(distance)
2 0 LOAD_FAST 2 (_norm)
2 LOAD_FAST 0 (pointA)
4 LOAD_FAST 1 (pointB)
6 BINARY_SUBTRACT
8 CALL_FUNCTION 1
10 RETURN_VALUE
накладные расходы на вызов функции по-прежнему составляют некоторую работу. И вы захотите сделать тесты, чтобы определить, можете ли вы лучше делать математику самостоятельно:
def distance(pointX, pointY):
return (
((pointX.x - pointY.x) ** 2) +
((pointY.y - pointY.y) ** 2) +
((pointZ.z - pointZ.z) ** 2)
) ** 0.5 # fast sqrt
на некоторых платформах, **0.5 быстрее math.sqrt. Ваш пробег может отличаться.
**** расширенный примечания к производительности.
почему вы вычисляете расстояние? Если единственная цель состоит в том, чтобы отобразить его,
print("The target is %.2fm away" % (distance(a, b)))
двигаться вдоль. Но если вы сравниваете расстояния,проверяете дальность и т. д., Я хотел бы добавить некоторые полезные наблюдения за производительностью.
возьмем два случая: сортировка по расстоянию или отбраковка списка на элементы, удовлетворяющие ограничению диапазона.
# Ultra naive implementations. Hold onto your hat.
def sort_things_by_distance(origin, things):
return things.sort(key=lambda thing: distance(origin, thing))
def in_range(origin, range, things):
things_in_range = []
for thing in things:
if distance(origin, thing) <= range:
things_in_range.append(thing)
первое, что нам нужно помнить, что мы используем Пифагор для расчета расстояния (dist = sqrt(x^2 + y^2 + z^2)) таким образом, мы делаем много sqrt звонки. Математика 101:
dist = root ( x^2 + y^2 + z^2 )
:.
dist^2 = x^2 + y^2 + z^2
and
sq(N) < sq(M) iff M > N
and
sq(N) > sq(M) iff N > M
and
sq(N) = sq(M) iff N == M
короче говоря: пока нам не потребуется расстояние в единице X, а не X^2, мы можем исключить самую сложную часть вычислений.
# Still naive, but much faster.
def distance_sq(left, right):
""" Returns the square of the distance between left and right. """
return (
((left.x - right.x) ** 2) +
((left.y - right.y) ** 2) +
((left.z - right.z) ** 2)
)
def sort_things_by_distance(origin, things):
return things.sort(key=lambda thing: distance_sq(origin, thing))
def in_range(origin, range, things):
things_in_range = []
# Remember that sqrt(N)**2 == N, so if we square
# range, we don't need to root the distances.
range_sq = range**2
for thing in things:
if distance_sq(origin, thing) <= range_sq:
things_in_range.append(thing)
отлично, обе функции больше не делают никаких дорогих squareroots. Это будет намного быстрее. Мы также можем улучшить in_range, преобразовав его в генератор:
def in_range(origin, range, things):
range_sq = range**2
yield from (thing for thing in things
if distance_sq(origin, thing) <= range_sq)
это особенно выгодно, если вы делаем что-то вроде:
if any(in_range(origin, max_dist, things)):
...
но если следующее, что вы собираетесь сделать, требует расстояния,
for nearby in in_range(origin, walking_distance, hotdog_stands):
print("%s %.2fm" % (nearby.name, distance(origin, nearby)))
рассмотрим уступчивые кортежи:
def in_range_with_dist_sq(origin, range, things):
range_sq = range**2
for thing in things:
dist_sq = distance_sq(origin, thing)
if dist_sq <= range_sq: yield (thing, dist_sq)
это может быть особенно полезно, если вы можете проверить диапазон цепей ("найти вещи, которые находятся рядом с X и в пределах Nm от Y", так как вам не нужно снова вычислять расстояние).
но что, если мы ищем действительно большой список things и мы ожидаем их много не стоит внимания?
на самом деле существует очень простая оптимизация:
def in_range_all_the_things(origin, range, things):
range_sq = range**2
for thing in things:
dist_sq = (origin.x - thing.x) ** 2
if dist_sq <= range_sq:
dist_sq += (origin.y - thing.y) ** 2
if dist_sq <= range_sq:
dist_sq += (origin.z - thing.z) ** 2
if dist_sq <= range_sq:
yield thing
полезно ли это будет зависеть от размера "вещей".
def in_range_all_the_things(origin, range, things):
range_sq = range**2
if len(things) >= 4096:
for thing in things:
dist_sq = (origin.x - thing.x) ** 2
if dist_sq <= range_sq:
dist_sq += (origin.y - thing.y) ** 2
if dist_sq <= range_sq:
dist_sq += (origin.z - thing.z) ** 2
if dist_sq <= range_sq:
yield thing
elif len(things) > 32:
for things in things:
dist_sq = (origin.x - thing.x) ** 2
if dist_sq <= range_sq:
dist_sq += (origin.y - thing.y) ** 2 + (origin.z - thing.z) ** 2
if dist_sq <= range_sq:
yield thing
else:
... just calculate distance and range-check it ...
и снова рассмотрите возможность получения dist_sq. Наш пример хот-дога тогда становится:
# Chaining generators
info = in_range_with_dist_sq(origin, walking_distance, hotdog_stands)
info = (stand, dist_sq**0.5 for stand, dist_sq in info)
for stand, dist in info:
print("%s %.2fm" % (stand, dist))
Я нахожу функцию "dist" в matplotlib.mlab, но я не думаю, что это достаточно удобно.
Я размещаю его здесь только для справки.
import numpy as np
import matplotlib as plt
a = np.array([1, 2, 3])
b = np.array([2, 3, 4])
# Distance between a and b
dis = plt.mlab.dist(a, b)
Это можно сделать следующим образом. Я не знаю, насколько это быстро, но он не использует NumPy.
from math import sqrt
a = (1, 2, 3) # Data point 1
b = (4, 5, 6) # Data point 2
print sqrt(sum( (a - b)**2 for a, b in zip(a, b)))
хороший один-лайнер:
dist = numpy.linalg.norm(a-b)
однако, если скорость является проблемой, я бы рекомендовал экспериментировать на вашей машине. Я обнаружил, что с помощью math библиотеки sqrt С ** оператор для квадрата намного быстрее на моей машине, чем однослойное решение NumPy.
я провел свои тесты с помощью этой простой программы:
#!/usr/bin/python
import math
import numpy
from random import uniform
def fastest_calc_dist(p1,p2):
return math.sqrt((p2[0] - p1[0]) ** 2 +
(p2[1] - p1[1]) ** 2 +
(p2[2] - p1[2]) ** 2)
def math_calc_dist(p1,p2):
return math.sqrt(math.pow((p2[0] - p1[0]), 2) +
math.pow((p2[1] - p1[1]), 2) +
math.pow((p2[2] - p1[2]), 2))
def numpy_calc_dist(p1,p2):
return numpy.linalg.norm(numpy.array(p1)-numpy.array(p2))
TOTAL_LOCATIONS = 1000
p1 = dict()
p2 = dict()
for i in range(0, TOTAL_LOCATIONS):
p1[i] = (uniform(0,1000),uniform(0,1000),uniform(0,1000))
p2[i] = (uniform(0,1000),uniform(0,1000),uniform(0,1000))
total_dist = 0
for i in range(0, TOTAL_LOCATIONS):
for j in range(0, TOTAL_LOCATIONS):
dist = fastest_calc_dist(p1[i], p2[j]) #change this line for testing
total_dist += dist
print total_dist
на моей машине, math_calc_dist работает намного быстрее, чем numpy_calc_dist: 1,5 секунд и 23.5 секунды!--23-->.
чтобы получить измеримую разницу между fastest_calc_dist и math_calc_dist мне пришлось встать TOTAL_LOCATIONS до 6000. Тогда fastest_calc_dist принимает ~50 секунд пока math_calc_dist принимает ~60 секунд.
вы также можете поэкспериментировать с numpy.sqrt и numpy.square хотя оба были медленнее, чем math альтернативы на моей машине.
мои тесты были запущены с Python 2.6.6.
вы можете просто вычесть векторы, а затем innerproduct.
следуя твоему примеру,
a = numpy.array((xa, ya, za))
b = numpy.array((xb, yb, zb))
tmp = a - b
sum_squared = numpy.dot(tmp.T, tmp)
result sqrt(sum_squared)
Это простой код и легко понять.
Мне нравится np.точка (точка продукта):
a = numpy.array((xa,ya,za))
b = numpy.array((xb,yb,zb))
distance = (np.dot(a-b,a-b))**.5
вот краткий код для евклидова расстояния в Python, учитывая две точки, представленные в виде списков в Python.
def distance(v1,v2):
return sum([(x-y)**2 for (x,y) in zip(v1,v2)])**(0.5)
import numpy as np
from scipy.spatial import distance
input_arr = np.array([[0,3,0],[2,0,0],[0,1,3],[0,1,2],[-1,0,1],[1,1,1]])
test_case = np.array([0,0,0])
dst=[]
for i in range(0,6):
temp = distance.euclidean(test_case,input_arr[i])
dst.append(temp)
print(dst)
вы можете легко использовать формулу
distance = np.sqrt(np.sum(np.square(a-b)))
который фактически ничего не делает, кроме использования теоремы Пифагора для вычисления расстояния, добавляя квадраты Δx, Δy и Δz и укореняя результат.
Если вы хотите найти расстояние до определенной точки от первого из сокращений, которые вы можете использовать, плюс вы можете сделать это с таким количеством измерений, как вы хотите.
import numpy as np
A = [3,4]
Dis = np.sqrt(A[0]**2 + A[1]**2)
вычислить Евклидово расстояние в многомерном пространстве:
import math
x = [1, 2, 6]
y = [-2, 3, 2]
dist = math.sqrt(sum([(xi-yi)**2 for xi,yi in zip(x, y)]))
5.0990195135927845
сначала найдите разность двух матриц. Затем примените умножение по элементам с помощью команды numpy multiply. После этого найдите суммирование элемента, умноженного на новую матрицу. Наконец, найдите квадратный корень из суммирования.
def findEuclideanDistance(a, b):
euclidean_distance = a - b
euclidean_distance = np.sum(np.multiply(euclidean_distance, euclidean_distance))
euclidean_distance = np.sqrt(euclidean_distance)
return euclidean_distance