Как мы можем выполнить слияние 8 элементов только с 16 сравнениями?
Ну, я задал вопрос о сортировке несколько дней назад. Я узнал, как доказать, что наименьшее количество сравнений путем сортировки 8 элементов равно 16, и я понял, почему. Но мой алгоритм сортировки слиянием насчитывает 17 сравнений, и в моем случае это правильно. Чтобы объединить два отсортированных массива длиной x и y каждый, нам нужно (x+y)-1 сравнение, поэтому в merge sort мы получаем 17 сравнений. Но это должно быть возможно с 16 сравнениями, так.. как? где я могу сохранить это сравнение 1).
здесь изображение:
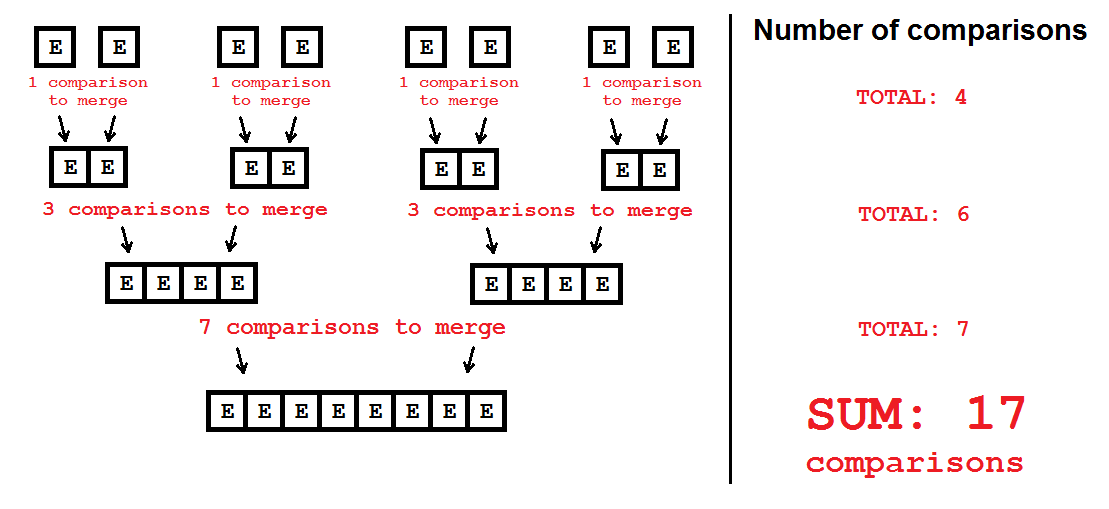
спасибо!
3 ответов
OP содержит четкое доказательство того, что сортировка слиянием из 8 элементов невозможно с менее чем 17 сравнениями. Тем не менее, можно отсортировать 8 элементов в 16 сравнениях с другим алгоритмом. Алгоритм описан в книге Д. кнута "искусство компьютерного программирования", Том 3, Глава 5.3.1. Он называется слияние вставки.
наименьшее количество сравнений не делает этот алгоритм самым быстрым. Например, дозатор чет–нечет сортировка слиянием С 19 сравнениями легко превосходит слияние вставки потому что он выполняет большинство сравнений параллельно.
вы можете получить наименьшее решение только тогда, когда у вас есть нечетное количество чисел для сортировки.
вы можете доказать, что 16 сравнений недостаточно, попробовав все возможные алгоритмы. Для этого вам понадобится и "алгоритм генерации алгоритма".
