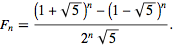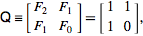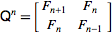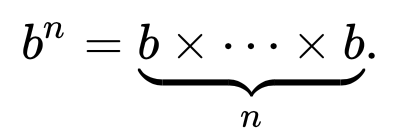Как написать последовательность Фибоначчи?
Я изначально неправильно закодировал программу. Вместо того, чтобы возвращать числа Фибоначчи между диапазоном (т. е. startNumber 1, endNumber 20 должен = только те числа между 1 и 20), я написал для программы, чтобы отобразить все числа Фибоначчи между диапазоном(т. е. startNumber 1, endNumber 20 отображает = первые 20 чисел Фибоначчи). Я думал, у меня есть верный код. Я тоже не понимаю, почему это происходит.
startNumber = int(raw_input("Enter the start number here "))
endNumber = int(raw_input("Enter the end number here "))
def fib(n):
if n < 2:
return n
return fib(n-2) + fib(n-1)
print map(fib, range(startNumber, endNumber))
кто-то указал в моей части II (которая была закрыто за дубликат ... https://stackoverflow.com/questions/504193/how-to-write-the-fibonacci-sequence-in-python-part-ii) что мне нужно передать startNumber и endNumber через генератор, используя цикл while. Кто-нибудь может указать мне, как это сделать? Любая помощь приветствуется.
Я обучающийся программист, и я столкнулся с некоторой путаницей. Меня просят написать программу, которая будет вычислять и отображать последовательность Фибоначчи в пользователь ввел начальный номер и конечный номер (т. е. startNumber = 20 endNumber = 100, и он будет отображать только числа между этим диапазоном). Фокус в том, чтобы использовать его включительно (что я не знаю, как сделать в Python? - Я предполагаю, что это означает использовать диапазон?).
то, что у меня пока нет фактического кодирования, а скорее:
- напишите формулу последовательности Fib в infinite
- отображение startNumber в endNumber только из Fib последовательность.
Я понятия не имею, с чего начать, и я прошу идеи или понимание того, как это написать. Я также попытался написать последовательность Fib forumla, но я теряюсь и на этом.
30 ответов
есть много информации о последовательности Фибоначчи на Википедия и вольфрам. Намного больше, чем тебе нужно. В любом случае, хорошо научиться использовать эти ресурсы, чтобы найти (быстро, если это возможно) то, что вам нужно.
напишите формулу последовательности Fib в infinite
в математике это дается в рекурсивной форме:
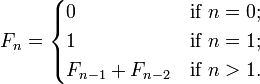
в программировании, бесконечный не существует. Вы можете использовать рекурсивная форма, переводящая математическую форму непосредственно на ваш язык, например, в Python она становится:
def F(n):
if n == 0: return 0
elif n == 1: return 1
else: return F(n-1)+F(n-2)
попробуйте на своем любимом языке и убедитесь, что эта форма требует большое времени как N становится больше. На самом деле, это O (2n) во времени.
перейдите на сайты, которые я связал с вами, и увидите это (on вольфрам):
Это довольно легко реализуйте и очень, очень быстро вычисляйте в Python:
from math import sqrt
def F(n):
return ((1+sqrt(5))**n-(1-sqrt(5))**n)/(2**n*sqrt(5))
другой способ сделать это, следуя определению (с Википедия):
первое число последовательности равно 0, второе число-1, и каждое последующее число равно сумме двух предыдущих чисел сама последовательность, дающая последовательность 0, 1, 1, 2, 3, 5, 8, etc.
если ваш язык поддерживает итераторы можно сделать что-то вроде:
def F():
a,b = 0,1
while True:
yield a
a, b = b, a + b
отображение startNumber в endNumber только из последовательности Fib.
как только вы знаете, как генерировать числа Фибоначчи, вам просто нужно цикл через числа и проверить, проверяют ли они данные условия.
предположим, теперь вы написали f (n), который возвращает n-й член последовательности Фибоначчи(например, с sqrt (5) )
в большинстве языков вы можете сделать что-то вроде:
def SubFib(startNumber, endNumber):
n = 0
cur = f(n)
while cur <= endNumber:
if startNumber <= cur:
print cur
n += 1
cur = f(n)
в python я бы использовал форма итератора и перейти к:
def SubFib(startNumber, endNumber):
for cur in F():
if cur > endNumber: return
if cur >= startNumber:
yield cur
for i in SubFib(10, 200):
print i
мой намек на научиться читать то, что вам нужно. Проект Euler (google for it) научит вас делать это: P Удачи и получайте удовольствие!
эффективный Питонический генератор последовательности Фибоначчи
я нашел этот вопрос, пытаясь получить кратчайшее Питоновское поколение этой последовательности (позже я понял, что видел подобное в Предложение По Улучшению Python), и я не заметил, чтобы кто - то еще придумал мое конкретное решение (хотя верхний ответ приближается, но все же менее элегантный), поэтому вот он, с комментариями, описывающими первую итерацию, потому что я думаю, что это может помочь читатели понимают:
def fib():
a, b = 0, 1
while True: # First iteration:
yield a # yield 0 to start with and then
a, b = b, a + b # a will now be 1, and b will also be 1, (0 + 1)
и использование:
for index, fibonacci_number in zip(range(10), fib()):
print('{i:3}: {f:3}'.format(i=index, f=fibonacci_number))
принты:
0: 0
1: 1
2: 1
3: 2
4: 3
5: 5
6: 8
7: 13
8: 21
9: 34
10: 55
(для целей атрибуции, я недавно заметил реализации в документации Python по модулям, даже используя переменные a и b, который я теперь помню, видел перед написанием этого ответа. Но я думаю, что этот ответ демонстрирует лучшее использование языка.)
рекурсивное определение реализация
на онлайн-энциклопедия целочисленных последовательностей определяет последовательность Фибоначчи рекурсивно как
F(n) = F(n-1) + F(n-2) с F(0) = 0 и F (1) = 1
краткое определение этого рекурсивно в Python можно сделать следующим образом:
def rec_fib(n):
'''inefficient recursive function as defined, returns Fibonacci number'''
if n > 1:
return rec_fib(n-1) + rec_fib(n-2)
return n
но это точное представление математического определения невероятно неэффективно для чисел, намного превышающих 30, потому что каждое число вычисляемый должен также вычислять для каждого числа ниже него. Вы можете продемонстрировать, насколько он медленный, используя следующее:
for i in range(40):
print(i, rec_fib(i))
Memoized рекурсия для эффективности
его можно запомнить для повышения скорости (в этом примере используется тот факт, что аргумент ключевого слова по умолчанию является одним и тем же объектом каждый раз, когда вызывается функция, но обычно вы не будете использовать изменяемый аргумент по умолчанию именно по этой причине):
def mem_fib(n, _cache={}):
'''efficiently memoized recursive function, returns a Fibonacci number'''
if n in _cache:
return _cache[n]
elif n > 1:
return _cache.setdefault(n, mem_fib(n-1) + mem_fib(n-2))
return n
вы найдете memoized версия намного быстрее, и быстро превысит максимальную глубину рекурсии, прежде чем вы можете даже думать, чтобы встать на кофе. Вы можете увидеть, насколько быстрее это визуально, делая это:
for i in range(40):
print(i, mem_fib(i))
(может показаться, что мы можем просто сделать ниже, но на самом деле это не позволяет нам воспользоваться кэшем, потому что он вызывает себя до вызова setdefault.)
def mem_fib(n, _cache={}):
'''don't do this'''
if n > 1:
return _cache.setdefault(n, mem_fib(n-1) + mem_fib(n-2))
return n
рекурсивно определенный генератор:
как я учился Haskell, я пришел через эту реализацию в Haskell:
fib@(0:tfib) = 0:1: zipWith (+) fib tfib
самое близкое, что я думаю, я могу получить к этому в Python на данный момент:
from itertools import tee
def fib():
yield 0
yield 1
# tee required, else with two fib()'s algorithm becomes quadratic
f, tf = tee(fib())
next(tf)
for a, b in zip(f, tf):
yield a + b
этот пример демонстрирует это:
[f for _, f in zip(range(999), fib())]
он может доходить только до предела рекурсии. Обычно 1000, тогда как версия Haskell может доходить до 100 миллионов, хотя для этого она использует все 8 ГБ памяти моего ноутбука:
> length $ take 100000000 fib
100000000
почему бы просто не сделать следующее?
x = [1,1]
for i in range(2, 10):
x.append(x[-1] + x[-2])
print(', '.join(str(y) for y in x))
идея последовательности Фибоначчи показана в следующем коде Python:
def fib(n):
if n == 1:
return 1
elif n == 0:
return 0
else:
return fib(n-1) + fib(n-2)
это означает, что fib-это функция, которая может делать одну из трех вещей. Он определяет fib(1) == 1, fib(0) == 0 и fib (n) как:
fib(n-1) + fib (n-2)
где N-произвольное целое число. Это означает, что fib (2), например, расширяется до следующей арифметики:
fib(2) = fib(1) + fib(0)
fib(1) = 1
fib(0) = 0
# Therefore by substitution:
fib(2) = 1 + 0
fib(2) = 1
мы можем вычислить fib (3) таким же образом с показанной арифметикой ниже:
fib(3) = fib(2) + fib(1)
fib(2) = fib(1) + fib(0)
fib(2) = 1
fib(1) = 1
fib(0) = 0
# Therefore by substitution:
fib(3) = 1 + 1 + 0
важно понимать, что fib(3) не может быть вычислен без вычисления fib(2), который вычисляется, зная определения fib(1) и fib (0). Наличие вызова функции, как функция Фибоначчи, называется рекурсией, и это важная тема в программировании.
Это звучит как домашнее задание, поэтому я не собираюсь делать начальную и конечную часть для вас. Python-удивительно выразительный язык для этого, хотя, поэтому это должно иметь смысл, если вы понимаете математику и, надеюсь, научите вас рекурсии. Удачи!
Edit: одна потенциальная критика моего кода заключается в том, что он не использует супер-удобную функцию Python, что делает функцию fib(n) намного короче. Мой пример немного более общий, хотя, поскольку не так много языков за пределами Python на самом деле имеют выход.
задачи :
функция кэширования уменьшает нормальный способ вычисления рядов Фибоначчи от O (2^n) to O (n) путем исключения повторений в рекурсивном дереве рядов Фибоначчи:
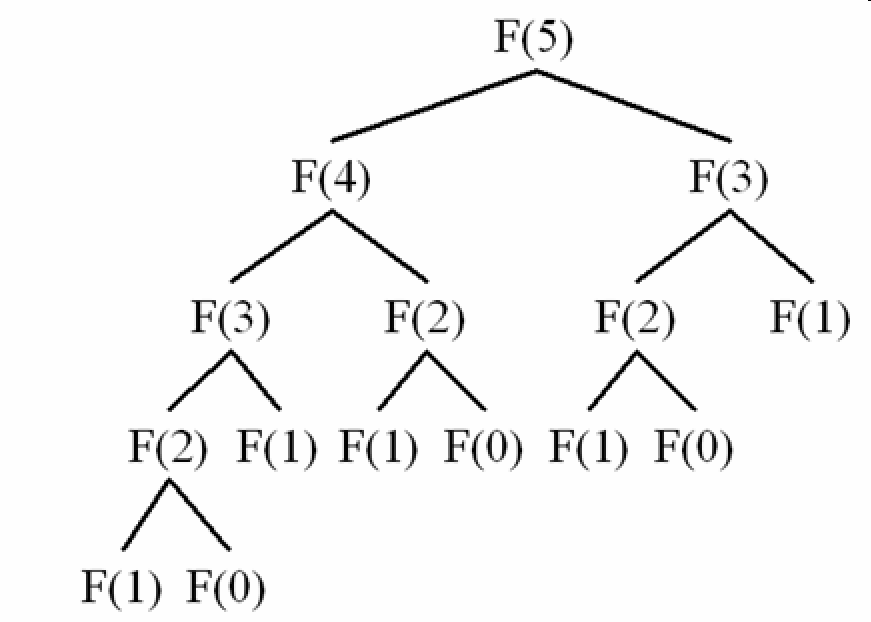
код :
import sys
table = [0]*1000
def FastFib(n):
if n<=1:
return n
else:
if(table[n-1]==0):
table[n-1] = FastFib(n-1)
if(table[n-2]==0):
table[n-2] = FastFib(n-2)
table[n] = table[n-1] + table[n-2]
return table[n]
def main():
print('Enter a number : ')
num = int(sys.stdin.readline())
print(FastFib(num))
if __name__=='__main__':
main()
Это довольно эффективно, используя o (log n) основные арифметические операции.
def fib(n):
return pow(2 << n, n + 1, (4 << 2*n) - (2 << n) - 1) % (2 << n)
этот использует O (1) основные арифметические операции, но размер промежуточных результатов велик и поэтому совсем не эффективен.
def fib(n):
return (4 << n*(3+n)) // ((4 << 2*n) - (2 << n) - 1) & ((2 << n) - 1)
этот вычисляет X^n в кольце полиномов Z[X] / (X^2 - X - 1), используя возведение в квадрат. Результатом этого вычисления является полином Fib(n)X + Fib(n-1), из которого может быть n-е число Фибоначчи читать.
опять же, это использует o (log n) арифметические операции и очень эффективно.
def mul(a, b):
return a[0]*b[1]+a[1]*b[0]+a[0]*b[0], a[0]*b[0]+a[1]*b[1]
def fib(n):
x, r = (1, 0), (0, 1)
while n:
if n & 1: r = mul(r, x)
x = mul(x, x)
n >>= 1
return r[0]
канонический код Python для печати последовательности Фибоначчи:
a,b=1,1
while(True):
print a,
a,b=b,a+b # Could also use b=a+b;a=b-a
для задачи "выведите первое число Фибоначчи длиной более 1000 цифр":
a,b=1,1
i=1
while(len(str(a))<=1000):
i=i+1
a,b=b,a+b
print i,len(str(a)),a
использование для цикла и печати только результата
def fib(n:'upto n number')->int:
if n==0:
return 0
elif n==1:
return 1
a=0
b=1
for i in range(0,n-1):
b=a+b
a=b-a
return b
результат
>>>fib(50)
12586269025
>>>>
>>> fib(100)
354224848179261915075
>>>
печатать list содержащий все цифры
def fib(n:'upto n number')->int:
l=[0,1]
if n==0:
return l[0]
elif n==1:
return l
a=0
b=1
for i in range(0,n-1):
b=a+b
a=b-a
l.append(b)
return l
результат
>>> fib(10)
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
существует очень простой способ понять это!
вы можете свободно запускать этот код в интернете с помощьюhttp://www.learnpython.org/
# Set the variable brian on line 3!
def fib(n):
"""This is documentation string for function. It'll be available by fib.__doc__()
Return a list containing the Fibonacci series up to n."""
result = []
a = 0
b = 1
while a < n:
result.append(a) # 0 1 1 2 3 5 8 (13) break
tmp_var = b # 1 1 2 3 5 8 13
b = a + b # 1 2 3 5 8 13 21
a = tmp_var # 1 1 2 3 5 8 13
# print(a)
return result
print(fib(10))
# result should be this: [0, 1, 1, 2, 3, 5, 8]
использовать рекурсию:
def fib(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
x=input('which fibonnaci do you want?')
print fib(x)
известно, что
и что n-я сила этой матрицы дает нам:
таким образом, мы можем реализовать функцию, которая просто вычисляет мощность этой матрицы до n-й -1 степени.
как все мы знаем, мощность a^n равна
таким образом, в конце функция Фибоначчи будет O( n )... ничего действительно отличающегося от более простая реализация, если бы не тот факт, что мы также знаем, что x^n * x^n = x^2n и оценки x^n поэтому можно сделать со сложностью O (log n )
вот моя реализация Фибоначчи с использованием языка программирования swift:
struct Mat {
var m00: Int
var m01: Int
var m10: Int
var m11: Int
}
func pow(m: Mat, n: Int) -> Mat {
guard n > 1 else { return m }
let temp = pow(m: m, n: n/2)
var result = matMultiply(a: temp, b: temp)
if n%2 != 0 {
result = matMultiply(a: result, b: Mat(m00: 1, m01: 1, m10: 1, m11: 0))
}
return result
}
func matMultiply(a: Mat, b: Mat) -> Mat {
let m00 = a.m00 * b.m00 + a.m01 * b.m10
let m01 = a.m00 * b.m01 + a.m01 * b.m11
let m10 = a.m10 * b.m00 + a.m11 * b.m10
let m11 = a.m10 * b.m01 + a.m11 * b.m11
return Mat(m00: m00, m01: m01, m10: m10, m11: m11)
}
func fibonacciFast(n: Int) -> Int {
guard n > 0 else { return 0 }
let m = Mat(m00: 1, m01: 1, m10: 1, m11: 0)
return pow(m: m, n: n-1).m00
}
это имеет сложность O (log n). Мы вычисляем oìpower Q с показателем N-1, а затем берем элемент m00, который является Fn+1, что при показателе мощности n-1 является именно n-м числом Фибоначчи мы желаемый.
как только у вас есть быстрая функция Фибоначчи, вы можете перебирать начальное и конечное число, чтобы получить интересующую вас часть последовательности Фибоначчи.
let sequence = (start...end).map(fibonacciFast)
конечно, сначала выполните некоторую проверку начала и конца, чтобы убедиться, что они могут сформировать допустимый диапазон.
Я знаю, что вопрос 8 лет, но мне было весело отвечать в любом случае. :)
def fib():
a,b = 1,1
num=eval(input("Please input what Fib number you want to be calculated: "))
num_int=int(num-2)
for i in range (num_int):
a,b=b,a+b
print(b)
все это выглядит немного сложнее, чем должно быть. Мой код очень прост и быстр:
def fibonacci(x):
List = []
f = 1
List.append(f)
List.append(f) #because the fibonacci sequence has two 1's at first
while f<=x:
f = List[-1] + List[-2] #says that f = the sum of the last two f's in the series
List.append(f)
else:
List.remove(List[-1]) #because the code lists the fibonacci number one past x. Not necessary, but defines the code better
for i in range(0, len(List)):
print List[i] #prints it in series form instead of list form. Also not necessary
другой способ сделать это:
a,n=[0,1],10
map(lambda i: reduce(lambda x,y: a.append(x+y),a[-2:]),range(n-2))
присвоение списка 'a', присвоение целого числа 'n' Map и reduce-это 2 из трех самых мощных функций в python. Здесь карта используется только для итерации "n-2" раз. a[-2:] получит последние два элемента массива. a.append (x+y) добавит последние два элемента и добавит к массиву
OK.. после того, как устали ссылаться на все длинные ответы, теперь найдите ниже sort & sweet, довольно прямой путь для реализации Фибоначчи в python. Вы можете улучшить его так, как хотите, получив аргумент или получив пользовательский ввод...или изменить ограничения с 10000. Как вам нужно......
def fibonacci():
start = 0
i = 1
lt = []
lt.append(start)
while start < 10000:
start += i
lt.append(start)
i = sum(lt[-2:])
lt.append(i)
print "The Fibonaccii series: ", lt
этот подход также хорошо работает. Найдите run analytics ниже
In [10]: %timeit fibonacci
10000000 loops, best of 3: 26.3 ns per loop
import time
start_time = time.time()
#recursive solution
def fib(x, y, upperLimit):
return [x] + fib(y, (x+y), upperLimit) if x < upperLimit else [x]
#To test :
print(fib(0,1,40000000000000))
print("run time: " + str(time.time() - start_time))
результаты
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, 7778742049, 12586269025, 20365011074, 32951280099, 53316291173, 86267571272, 139583862445, 225851433717, 365435296162, 591286729879, 956722026041, 1548008755920, 2504730781961, 4052739537881, 6557470319842, 10610209857723, 17167680177565, 27777890035288, 44945570212853]
время работы: 0.04298138618469238
в основном переведено с Ruby:
def fib(n):
a = 0
b = 1
for i in range(1,n+1):
c = a + b
print c
a = b
b = c
...
def fib(lowerbound, upperbound):
x = 0
y = 1
while x <= upperbound:
if (x >= lowerbound):
yield x
x, y = y, x + y
startNumber = 10
endNumber = 100
for fib_sequence in fib(startNumber, endNumber):
print "And the next number is... %d!" % fib_sequence
последовательность Фибоначчи: 1, 1, 2, 3, 5, 8, ....
что это f(1) = 1, f(2) = 1, f(3) = 2, ..., f(n) = f(n-1) + f(n-2).
моя любимая реализация (самая простая и все же достигает скорости света по сравнению с другими реализациями) такова:
def fibonacci(n):
a, b = 0, 1
for _ in range(1, n):
a, b = b, a + b
return b
тест
>>> [fibonacci(i) for i in range(1, 10)]
[1, 1, 2, 3, 5, 8, 13, 21, 34]
времени
>>> %%time
>>> fibonacci(100**3)
CPU times: user 9.65 s, sys: 9.44 ms, total: 9.66 s
Wall time: 9.66 s
Edit:пример визуализации для этой реализации.
рекурсии увеличивает время. Чтобы устранить петли, сначала import math. Тогда используйте math.sqrt и золотое сечение в функции:
#!/usr/bin/env python3
import math
def fib(n):
gr = (1 + math.sqrt(5)) / 2
fib_first = (gr**n - (1 - gr)**n) / math.sqrt(5)
return int(round(fib_first))
fib_final = fib(100)
print(fib_final)
это улучшение ответа Мэтью Генри:
def fib(n):
a = 0
b = 1
for i in range(1,n+1):
c = a + b
print b
a = b
b = c
код должен печатать b вместо печати c
выход: 1,1,2,3,5 ....
Это самый простой в python для ряда Фибоначчи, но скорректированный [0] в выходном массиве с помощью append (), чтобы привести ко второй переменной списка результатов, которая является result.append(second)
def fibo(num):
first = 0
second = 1
result = [0]
print('Fibonacci series is')
for i in range(0,num):
third = first + second
#print(second)
result.append(second)
first = second
second = third
print(result)
return
fibo(7)
выход
Fibonacci series is
[0, 1, 1, 2, 3, 5, 8, 13]
Go узнайте, как преобразовать рекурсивную проблему в итеративную. Должен быть в состоянии вычислить оттуда.
Это могут быть принципы, которые они пытаются заставить вас учиться, особенно если это курс алгоритмов.
sum = 0
endingnumber = 1
print "\n.:Fibonacci sequence:.\n"
firstnumber = input("Enter the first number: ")
secondnumber = input("Enter the second number: ")
endingnumber = input("Enter the number to stop at: ")
if secondnumber < firstnumber:
print "\nSecond number must be bigger than the first number!!!\n"
else:
while sum <= endingnumber:
print firstnumber
if secondnumber > endingnumber:
break
else:
print secondnumber
sum = firstnumber + secondnumber
firstnumber = sum
secondnumber = secondnumber + sum
Как вы можете видеть, это действительно неэффективно, но это работает.
просто http://projecteuler.net/problem=2 это был мой взгляд на него
# Even Fibonacci numbers
# Problem 2
def get_fibonacci(size):
numbers = [1,2]
while size > len(numbers):
next_fibonacci = numbers[-1]+numbers[-2]
numbers.append(next_fibonacci)
print numbers
get_fibonacci(20)
def fib(x, y, n):
if n < 1:
return x, y, n
else:
return fib(y, x + y, n - 1)
print fib(0, 1, 4)
(3, 5, 0)
#
def fib(x, y, n):
if n > 1:
for item in fib(y, x + y, n - 1):
yield item
yield x, y, n
f = fib(0, 1, 12)
f.next()
(89, 144, 1)
f.next()[0]
55
Это было практическое задание, которое я видел на Sal Академии Хана по программированию на Python: https://www.khanacademy.org/science/computer-science-subject/computer-science/v/exercise---write-a-fibonacci-function
он, вероятно,не первый человек, чтобы назначить это как некоторую работу. Но это потрясающе, выяснить это самостоятельно. Я узнал много выяснить это на самом деле и это был взрыв.
Я рекомендую вам выяснить это самостоятельно перед попробуй скопировать чужой код для домашнего задания.
в видео выше, сал инструктор, показывает показывает всю теорию за числом Фибоначчи, и с учетом этого вы должны быть в состоянии понять это.
это заняло у меня около 10 минут, и это код, который я сделал (я изучаю Python, начиная с 3 дней назад, и это мой первый язык программирования для изучения). Я бы не смог написать код, если бы не видео из учебника раньше: https://www.khanacademy.org/science/computer-science-subject/computer-science/v/comparing-iterative-and-recursive-factorial-functions это дает пример того, как Sal делает рекурсивное факторное уравнение и дает вам ум, чтобы решить эту проблему.
вот мой код:
def fibonacci(num):
if num <= 1: #base case
return num
else:
return fibonacci(num-1) + fibonacci(num-2)
вы можете видеть, что если число равно 1 или 0, то вы просто возвращаете число.
Я нахожу это чище, чем говорить, если число 1 возвращает 1 и если число 0 возвращает 0.
может это поможет
def fibo(n):
result = []
a, b = 0, 1
while b < n:
result.append(b)
a, b = b, b + a
return result
попробуйте это:
def nth_fib(n):
if n == 0:
return 1
elif n == 1:
return 0
else:
return nth_fib(n - 1) + nth_fib(n - 2)
на основе классической последовательности Фибоначчи и только ради однострочных
Если вам как раз нужно номер индекса, то вы можете использовать уменьшение (даже если уменьшить это не лучше всего подходит для этого это может быть хорошее упражнение)
def fibonacci(index):
return reduce(lambda r,v: r.append(r[-1]+r[-2]) or (r.pop(0) and 0) or r , xrange(index), [0, 1])[1]
и чтобы получить полный набор просто удалить or (r.pop (0) и 0)
reduce(lambda r,v: r.append(r[-1]+r[-2]) or r , xrange(last_index), [0, 1])