Как нарисовать диаграмму рассеяния с линиями плотности контура в полярных координатах с помощью Matplotlib?

Я пытаюсь сделать точечную диаграмму в полярные координаты с контурными линиями, наложенными на облако точек. Я знаю, как это сделать в декартовых координатах, используя numpy.histogram2d: 

# Simple case: scatter plot with density contours in cartesian coordinates

import matplotlib.pyplot as pl
import numpy as np

np.random.seed(2015)
N = 1000
shift_value = -6.

x1 = np.random.randn(N) + shift_value
y1 = np.random.randn(N) + shift_value

fig, ax = pl.subplots(nrows=1,ncols=1)

ax.scatter(x1,y1,color='hotpink')

H, xedges, yedges = np.histogram2d(x1,y1)
extent = [xedges[0],xedges[-1],yedges[0],yedges[-1]]
cset1 = ax.contour(H,extent=extent)

# Modify xlim and ylim to be a bit more consistent with what's next
ax.set_xlim(xmin=-10.,xmax=+10.)
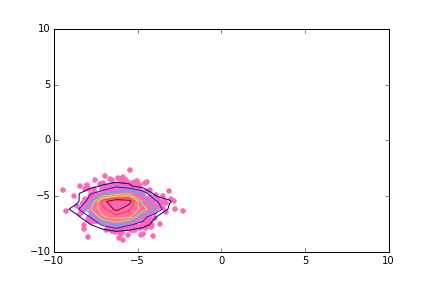
ax.set_ylim(ymin=-10.,ymax=+10.)

выход здесь:

correct_output_cartesian

однако, когда я пытаюсь перенести свой код на полярные координаты, я получаю искаженные контурные линии. Вот мой код и произведенный (неправильный) вывод:

# Case with polar coordinates; the contour lines are distorted

np.random.seed(2015)
N = 1000
shift_value = -6.

def CartesianToPolar(x,y):
    r = np.sqrt(x**2 + y**2)
    theta = np.arctan2(y,x)

    return theta, r

x2 = np.random.randn(N) + shift_value
y2 = np.random.randn(N) + shift_value

theta2, r2 = CartesianToPolar(x2,y2)

fig2 = pl.figure()
ax2 = pl.subplot(projection="polar")
ax2.scatter(theta2, r2, color='hotpink')

H, xedges, yedges = np.histogram2d(x2,y2)


theta_edges, r_edges = CartesianToPolar(xedges[:-1],yedges[:-1])
ax2.contour(theta_edges, r_edges,H)

на неправильно вывод здесь:

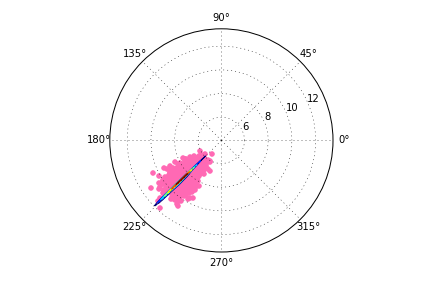
wrong_output_polar

есть ли способ иметь контурные линии в правильном масштабе?

EDIT для рассмотрения предложений, сделанных в комментариях.

EDIT2: кто-то предположил, что вопрос может быть дубликатом этот вопрос. Хотя я признаю, что проблемы схожи, моя касается конкретно построения контуров плотности точек над диаграммой рассеяния. Другой вопрос о том, как построить контур уровни любого количества, заданного вместе с координатами точек.

8
matplotlib polar-coordinates python scatter-plot

1 ответов

проблема в том, что вы конвертируете только края массива. Преобразуя только координаты X и y ребер, вы эффективно преобразуете координаты диагональной линии через 2D-массив. Эта линия имеет очень маленький диапазон theta значения, и вы применяете этот диапазон ко всей сетке.

быстрое (но неправильное) исправление

в большинстве случаев вы можете преобразовать всю сетку (т. е. 2D-массивы x и y, изготовления 2D массивы theta и r) в полярных координатах.

вместо:

H, xedges, yedges = np.histogram2d(x2,y2)
theta_edges, r_edges = CartesianToPolar(xedges[:-1],yedges[:-1])

сделать что-то похожее на:

H, xedges, yedges = np.histogram2d(x2,y2)
xedges, yedges = np.meshgrid(xedges[:-1],yedges[:-1]
theta_edges, r_edges = CartesianToPolar(xedges, yedges)

как пример:

import numpy as np
import matplotlib.pyplot as plt

def main():
    x2, y2 = generate_data()
    theta2, r2 = cart2polar(x2,y2)

    fig2 = plt.figure()
    ax2 = fig2.add_subplot(111, projection="polar")
    ax2.scatter(theta2, r2, color='hotpink')

    H, xedges, yedges = np.histogram2d(x2,y2)

    xedges, yedges = np.meshgrid(xedges[:-1], yedges[:-1])
    theta_edges, r_edges = cart2polar(xedges, yedges)
    ax2.contour(theta_edges, r_edges, H)

    plt.show()

def generate_data():
    np.random.seed(2015)
    N = 1000
    shift_value = -6.

    x2 = np.random.randn(N) + shift_value
    y2 = np.random.randn(N) + shift_value
    return x2, y2

def cart2polar(x,y):
    r = np.sqrt(x**2 + y**2)
    theta = np.arctan2(y,x)

    return theta, r

main()

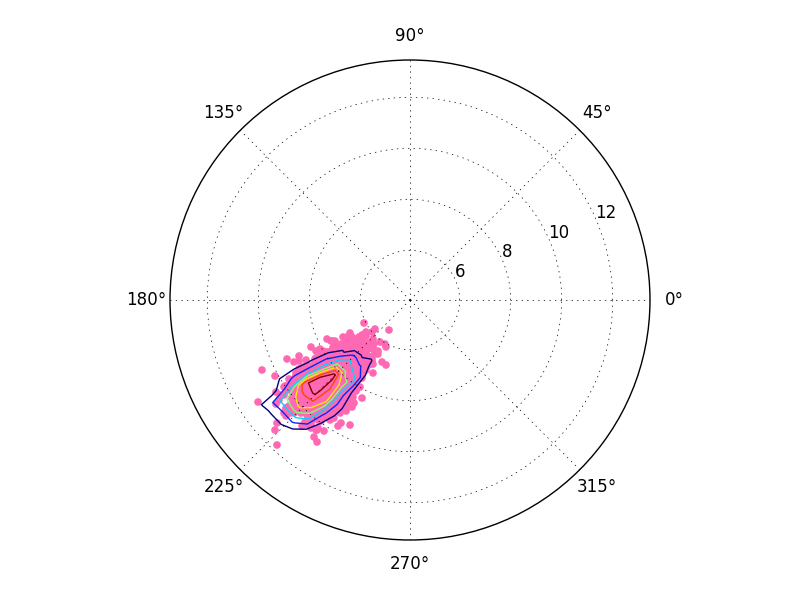
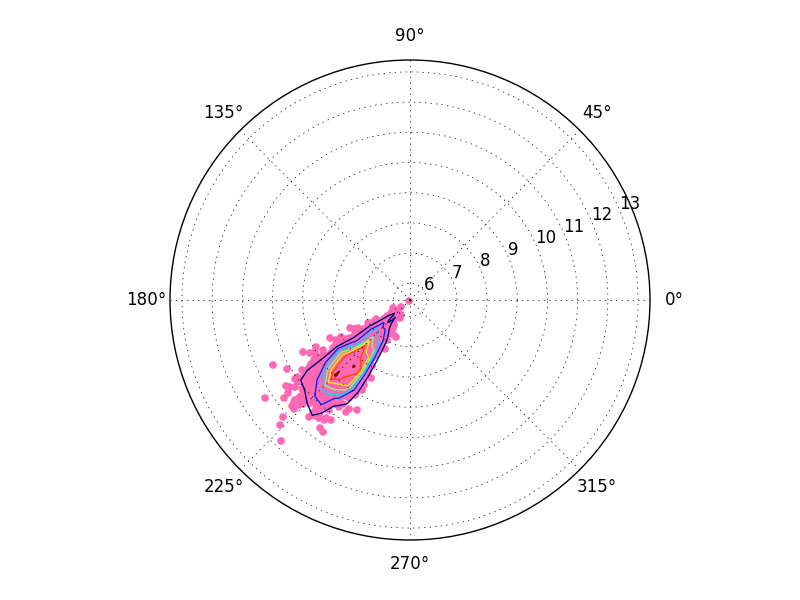
enter image description here

, вы можете заметить, что это выглядит немного неправильно. Это потому что ax.contour неявно предполагает, что входные данные на регулярной сетке. Мы дали ему регулярную сетку в декартовых координатах, но не регулярную сетку в полярных координирует. Предполагается, что мы прошли через обычную сетку в полярных координатах. Мы могли бы перепроверить сетку, но есть более простой способ.

правильное решение

чтобы правильно построить 2D-гистограмму, вычислите гистограмму в Полярном пространстве.

например, сделать что-то похожее на:

theta2, r2 = cart2polar(x2,y2)
H, theta_edges, r_edges = np.histogram2d(theta2, r2)
ax2.contour(theta_edges[:-1], r_edges[:-1], H)

как пример:

import numpy as np
import matplotlib.pyplot as plt

def main():
    x2, y2 = generate_data()
    theta2, r2 = cart2polar(x2,y2)

    fig2 = plt.figure()
    ax2 = fig2.add_subplot(111, projection="polar")
    ax2.scatter(theta2, r2, color='hotpink')

    H, theta_edges, r_edges = np.histogram2d(theta2, r2)
    ax2.contour(theta_edges[:-1], r_edges[:-1], H)

    plt.show()

def generate_data():
    np.random.seed(2015)
    N = 1000
    shift_value = -6.

    x2 = np.random.randn(N) + shift_value
    y2 = np.random.randn(N) + shift_value
    return x2, y2

def cart2polar(x,y):
    r = np.sqrt(x**2 + y**2)
    theta = np.arctan2(y,x)

    return theta, r

main()

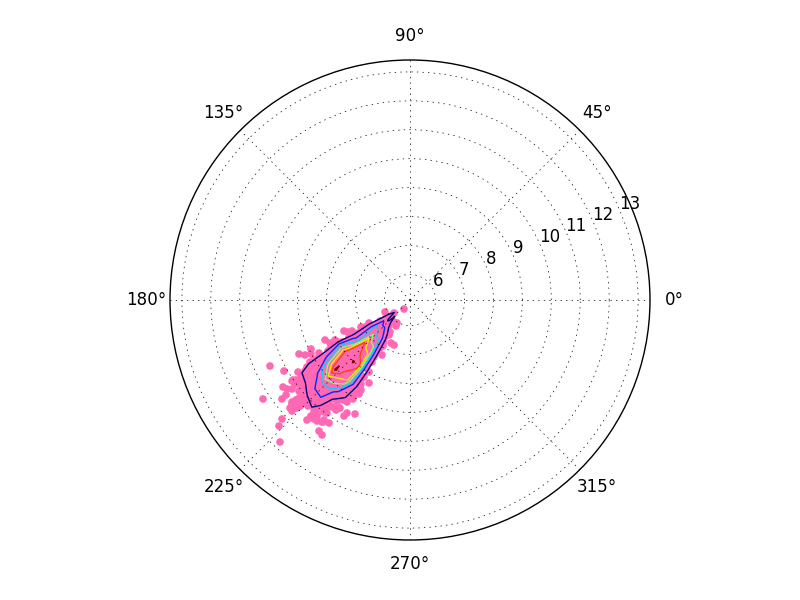
enter image description here

наконец, вы можете заметить небольшое изменение в приведенном выше результате. Это связано с соглашениями сетки, ориентированными на ячейки (x[0,0], y[0,0] дает центр ячейки) против ориентированных на ребро соглашений сетки (x[0,0], y[0,0] дает нижний левый угол ячейки. ax.contour ожидает, что все будет центрировано по ячейкам, но вы даете ему выровненные по краю значения x и y.

это всего лишь полуклеточный сдвиг, но если вы хотите его исправить, Сделайте что-то вроде:

def centers(bins):
    return np.vstack([bins[:-1], bins[1:]]).mean(axis=0)

H, theta_edges, r_edges = np.histogram2d(theta2, r2)
theta_centers, r_centers = centers(theta_edges), centers(r_edges)

ax2.contour(theta_centers, r_centers, H)

enter image description here

13