Как нарисовать перспективу-правильная сетка в 2D
У меня есть приложение, которое определяет прямоугольник реального мира поверх изображения / фотографии, конечно, в 2D это может быть не прямоугольник, потому что вы смотрите на него под углом.
проблема в том, что, скажем, прямоугольник должен иметь линии сетки, нарисованные на нем, например, если это 3x5, поэтому мне нужно нарисовать 2 линии со стороны 1 в сторону 3 и 4 линии со стороны 2 в сторону 4.
на данный момент я разбиваю каждую линию на равноудаленные части, чтобы начать и конечная точка всех линий сетки. Однако чем больше угол прямоугольника, тем более "неправильными" становятся эти линии, поскольку горизонтальные линии дальше от вас должны быть ближе друг к другу.
кто-нибудь знает название алгоритма, который я должен искать?
Да, я знаю, что вы можете сделать это в 3D, однако я ограничен 2D для этого конкретного приложения.
11 ответов
вот решение: http://freespace.virgin.net/hugo.elias/graphics/x_persp.htm
основная идея заключается в том, что вы можете найти правильный "центр" вашего прямоугольника, соединяя углы по диагонали. Пересечение двух результирующих линий-это ваш правильный центр перспективы. Оттуда вы разделяете свой прямоугольник на четыре меньших прямоугольника и повторяете процесс. Количество раз зависит от того, насколько точно вы хотите. Вы можете разделить чуть ниже размера пикселя для эффективной идеальной перспективы.
затем в subrectangles вы просто применить стандартный неисправленных "фактурная" треугольники, или прямоугольники, или что.
вы можете выполнить этот алгоритм, не вдаваясь в сложные проблемы построения "реального" 3d-мира. это также хорошо, если вы do имеют реальный 3D-мир, смоделированный, но ваши textriangles не являются перспективными исправленными в оборудовании, или вам нужен эффективный способ получить перспективные правильные плоскости без обмана рендеринга на пиксель.
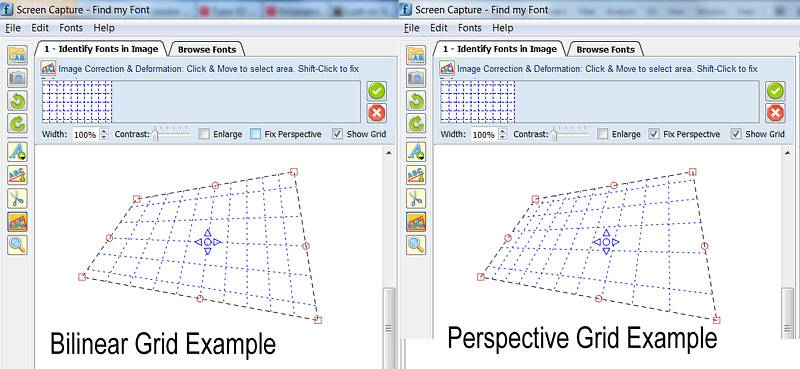 Изображение: пример билинейного и перспективного преобразования (Примечание: высота верхних и нижних горизонтальных линий сетки фактически составляет половину высоты остальных линий на обоих чертежах)
Изображение: пример билинейного и перспективного преобразования (Примечание: высота верхних и нижних горизонтальных линий сетки фактически составляет половину высоты остальных линий на обоих чертежах)
========================================
Я знаю, что это старый вопрос, но у меня есть общее решение, поэтому я решил опубликовать его, прыгая, это будет полезно для будущих читателей. Код ниже может нарисовать произвольную сетку перспективы без необходимости повторения вычисления.
Я начинаю с аналогичной проблемы: нарисовать 2D-сетку перспективы, а затем преобразовать изображение подчеркивания, чтобы восстановить перспективу.
Я начал читать здесь: http://www.imagemagick.org/Usage/distorts/#bilinear_forward
и потом здесь (библиотека Leptonica ): http://www.leptonica.com/affine.html
Я нашел это:
когда вы смотрите на объект в самолет из произвольного направления конечное расстояние, вы получаете дополнительное искажение" keystone " в изображение. Это проективное преобразование, которое сохраняет прямые линии прямой, но не сохраняет углы между линиями. Это коробление не может быть описана линейным аффинным преобразованием, и на самом деле отличается X-и y-зависимыми терминами в знаменателе.
преобразование не является линейным, как уже указывали многие люди в этом потоке. Он включает в себя решение линейной системы из 8 уравнений (один раз) для вычисления 8 необходимых коэффициентов, а затем вы можете использовать их для преобразования столько точек, сколько хотите.
чтобы избежать включения всей библиотеки Leptonica в мой проект, я взял из нее несколько фрагментов кода, удалил все специальные типы данных и макросы Leptonica, исправил некоторые утечки памяти и преобразовал ее в класс C++ (в основном по причинам инкапсуляции) , который делает только одну вещь: Он отображает координату a (Qt) qpointf float (x,y) в координату соответствующая перспективная координата.
Если вы хотите адаптировать код к другой библиотеке C++, единственное, что нужно переопределить / заменить, - это класс координат QPointF.
Я надеюсь, что некоторые будущие читатели найдут это полезным. Код ниже разделен на 3 части:
A. пример использования класса genImageProjective C++ для рисования 2D-сетки перспективы
B. genImageProjective.файл H
C. genImageProjective.СРР файл
//============================================================
// C++ Code Example on how to use the
// genImageProjective class to draw a perspective 2D Grid
//============================================================
#include "genImageProjective.h"
// Input: 4 Perspective-Tranformed points:
// perspPoints[0] = top-left
// perspPoints[1] = top-right
// perspPoints[2] = bottom-right
// perspPoints[3] = bottom-left
void drawGrid(QPointF *perspPoints)
{
(...)
// Setup a non-transformed area rectangle
// I use a simple square rectangle here because in this case we are not interested in the source-rectangle,
// (we want to just draw a grid on the perspPoints[] area)
// but you can use any arbitrary rectangle to perform a real mapping to the perspPoints[] area
QPointF topLeft = QPointF(0,0);
QPointF topRight = QPointF(1000,0);
QPointF bottomRight = QPointF(1000,1000);
QPointF bottomLeft = QPointF(0,1000);
float width = topRight.x() - topLeft.x();
float height = bottomLeft.y() - topLeft.y();
// Setup Projective trasform object
genImageProjective imageProjective;
imageProjective.sourceArea[0] = topLeft;
imageProjective.sourceArea[1] = topRight;
imageProjective.sourceArea[2] = bottomRight;
imageProjective.sourceArea[3] = bottomLeft;
imageProjective.destArea[0] = perspPoints[0];
imageProjective.destArea[1] = perspPoints[1];
imageProjective.destArea[2] = perspPoints[2];
imageProjective.destArea[3] = perspPoints[3];
// Compute projective transform coefficients
if (imageProjective.computeCoeefficients() != 0)
return; // This can actually fail if any 3 points of Source or Dest are colinear
// Initialize Grid parameters (without transform)
float gridFirstLine = 0.1f; // The normalized position of first Grid Line (0.0 to 1.0)
float gridStep = 0.1f; // The normalized Grd size (=distance between grid lines: 0.0 to 1.0)
// Draw Horizonal Grid lines
QPointF lineStart, lineEnd, tempPnt;
for (float pos = gridFirstLine; pos <= 1.0f; pos += gridStep)
{
// Compute Grid Line Start
tempPnt = QPointF(topLeft.x(), topLeft.y() + pos*width);
imageProjective.mapSourceToDestPoint(tempPnt, lineStart);
// Compute Grid Line End
tempPnt = QPointF(topRight.x(), topLeft.y() + pos*width);
imageProjective.mapSourceToDestPoint(tempPnt, lineEnd);
// Draw Horizontal Line (use your prefered method to draw the line)
(...)
}
// Draw Vertical Grid lines
for (float pos = gridFirstLine; pos <= 1.0f; pos += gridStep)
{
// Compute Grid Line Start
tempPnt = QPointF(topLeft.x() + pos*height, topLeft.y());
imageProjective.mapSourceToDestPoint(tempPnt, lineStart);
// Compute Grid Line End
tempPnt = QPointF(topLeft.x() + pos*height, bottomLeft.y());
imageProjective.mapSourceToDestPoint(tempPnt, lineEnd);
// Draw Vertical Line (use your prefered method to draw the line)
(...)
}
(...)
}
==========================================
//========================================
//C++ Header File: genImageProjective.h
//========================================
#ifndef GENIMAGE_H
#define GENIMAGE_H
#include <QPointF>
// Class to transform an Image Point using Perspective transformation
class genImageProjective
{
public:
genImageProjective();
int computeCoeefficients(void);
int mapSourceToDestPoint(QPointF& sourcePoint, QPointF& destPoint);
public:
QPointF sourceArea[4]; // Source Image area limits (Rectangular)
QPointF destArea[4]; // Destination Image area limits (Perspectivelly Transformed)
private:
static int gaussjordan(float **a, float *b, int n);
bool coefficientsComputed;
float vc[8]; // Vector of Transform Coefficients
};
#endif // GENIMAGE_H
//========================================
//========================================
//C++ CPP File: genImageProjective.cpp
//========================================
#include <math.h>
#include "genImageProjective.h"
// ----------------------------------------------------
// class genImageProjective
// ----------------------------------------------------
genImageProjective::genImageProjective()
{
sourceArea[0] = sourceArea[1] = sourceArea[2] = sourceArea[3] = QPointF(0,0);
destArea[0] = destArea[1] = destArea[2] = destArea[3] = QPointF(0,0);
coefficientsComputed = false;
}
// --------------------------------------------------------------
// Compute projective transform coeeeficients
// RetValue: 0: Success, !=0: Error
/*-------------------------------------------------------------*
* Projective coordinate transformation *
*-------------------------------------------------------------*/
/*!
* computeCoeefficients()
*
* Input: this->sourceArea[4]: (source 4 points; unprimed)
* this->destArea[4]: (transformed 4 points; primed)
* this->vc (computed vector of transform coefficients)
* Return: 0 if OK; <0 on error
*
* We have a set of 8 equations, describing the projective
* transformation that takes 4 points (sourceArea) into 4 other
* points (destArea). These equations are:
*
* x1' = (c[0]*x1 + c[1]*y1 + c[2]) / (c[6]*x1 + c[7]*y1 + 1)
* y1' = (c[3]*x1 + c[4]*y1 + c[5]) / (c[6]*x1 + c[7]*y1 + 1)
* x2' = (c[0]*x2 + c[1]*y2 + c[2]) / (c[6]*x2 + c[7]*y2 + 1)
* y2' = (c[3]*x2 + c[4]*y2 + c[5]) / (c[6]*x2 + c[7]*y2 + 1)
* x3' = (c[0]*x3 + c[1]*y3 + c[2]) / (c[6]*x3 + c[7]*y3 + 1)
* y3' = (c[3]*x3 + c[4]*y3 + c[5]) / (c[6]*x3 + c[7]*y3 + 1)
* x4' = (c[0]*x4 + c[1]*y4 + c[2]) / (c[6]*x4 + c[7]*y4 + 1)
* y4' = (c[3]*x4 + c[4]*y4 + c[5]) / (c[6]*x4 + c[7]*y4 + 1)
*
* Multiplying both sides of each eqn by the denominator, we get
*
* AC = B
*
* where B and C are column vectors
*
* B = [ x1' y1' x2' y2' x3' y3' x4' y4' ]
* C = [ c[0] c[1] c[2] c[3] c[4] c[5] c[6] c[7] ]
*
* and A is the 8x8 matrix
*
* x1 y1 1 0 0 0 -x1*x1' -y1*x1'
* 0 0 0 x1 y1 1 -x1*y1' -y1*y1'
* x2 y2 1 0 0 0 -x2*x2' -y2*x2'
* 0 0 0 x2 y2 1 -x2*y2' -y2*y2'
* x3 y3 1 0 0 0 -x3*x3' -y3*x3'
* 0 0 0 x3 y3 1 -x3*y3' -y3*y3'
* x4 y4 1 0 0 0 -x4*x4' -y4*x4'
* 0 0 0 x4 y4 1 -x4*y4' -y4*y4'
*
* These eight equations are solved here for the coefficients C.
*
* These eight coefficients can then be used to find the mapping
* (x,y) --> (x',y'):
*
* x' = (c[0]x + c[1]y + c[2]) / (c[6]x + c[7]y + 1)
* y' = (c[3]x + c[4]y + c[5]) / (c[6]x + c[7]y + 1)
*
*/
int genImageProjective::computeCoeefficients(void)
{
int retValue = 0;
int i;
float *a[8]; /* 8x8 matrix A */
float *b = this->vc; /* rhs vector of primed coords X'; coeffs returned in vc[] */
b[0] = destArea[0].x();
b[1] = destArea[0].y();
b[2] = destArea[1].x();
b[3] = destArea[1].y();
b[4] = destArea[2].x();
b[5] = destArea[2].y();
b[6] = destArea[3].x();
b[7] = destArea[3].y();
for (i = 0; i < 8; i++)
a[i] = NULL;
for (i = 0; i < 8; i++)
{
if ((a[i] = (float *)calloc(8, sizeof(float))) == NULL)
{
retValue = -100; // ERROR_INT("a[i] not made", procName, 1);
goto Terminate;
}
}
a[0][0] = sourceArea[0].x();
a[0][1] = sourceArea[0].y();
a[0][2] = 1.;
a[0][6] = -sourceArea[0].x() * b[0];
a[0][7] = -sourceArea[0].y() * b[0];
a[1][3] = sourceArea[0].x();
a[1][4] = sourceArea[0].y();
a[1][5] = 1;
a[1][6] = -sourceArea[0].x() * b[1];
a[1][7] = -sourceArea[0].y() * b[1];
a[2][0] = sourceArea[1].x();
a[2][1] = sourceArea[1].y();
a[2][2] = 1.;
a[2][6] = -sourceArea[1].x() * b[2];
a[2][7] = -sourceArea[1].y() * b[2];
a[3][3] = sourceArea[1].x();
a[3][4] = sourceArea[1].y();
a[3][5] = 1;
a[3][6] = -sourceArea[1].x() * b[3];
a[3][7] = -sourceArea[1].y() * b[3];
a[4][0] = sourceArea[2].x();
a[4][1] = sourceArea[2].y();
a[4][2] = 1.;
a[4][6] = -sourceArea[2].x() * b[4];
a[4][7] = -sourceArea[2].y() * b[4];
a[5][3] = sourceArea[2].x();
a[5][4] = sourceArea[2].y();
a[5][5] = 1;
a[5][6] = -sourceArea[2].x() * b[5];
a[5][7] = -sourceArea[2].y() * b[5];
a[6][0] = sourceArea[3].x();
a[6][1] = sourceArea[3].y();
a[6][2] = 1.;
a[6][6] = -sourceArea[3].x() * b[6];
a[6][7] = -sourceArea[3].y() * b[6];
a[7][3] = sourceArea[3].x();
a[7][4] = sourceArea[3].y();
a[7][5] = 1;
a[7][6] = -sourceArea[3].x() * b[7];
a[7][7] = -sourceArea[3].y() * b[7];
retValue = gaussjordan(a, b, 8);
Terminate:
// Clean up
for (i = 0; i < 8; i++)
{
if (a[i])
free(a[i]);
}
this->coefficientsComputed = (retValue == 0);
return retValue;
}
/*-------------------------------------------------------------*
* Gauss-jordan linear equation solver *
*-------------------------------------------------------------*/
/*
* gaussjordan()
*
* Input: a (n x n matrix)
* b (rhs column vector)
* n (dimension)
* Return: 0 if ok, 1 on error
*
* Note side effects:
* (1) the matrix a is transformed to its inverse
* (2) the vector b is transformed to the solution X to the
* linear equation AX = B
*
* Adapted from "Numerical Recipes in C, Second Edition", 1992
* pp. 36-41 (gauss-jordan elimination)
*/
#define SWAP(a,b) {temp = (a); (a) = (b); (b) = temp;}
int genImageProjective::gaussjordan(float **a, float *b, int n)
{
int retValue = 0;
int i, icol=0, irow=0, j, k, l, ll;
int *indexc = NULL, *indexr = NULL, *ipiv = NULL;
float big, dum, pivinv, temp;
if (!a)
{
retValue = -1; // ERROR_INT("a not defined", procName, 1);
goto Terminate;
}
if (!b)
{
retValue = -2; // ERROR_INT("b not defined", procName, 1);
goto Terminate;
}
if ((indexc = (int *)calloc(n, sizeof(int))) == NULL)
{
retValue = -3; // ERROR_INT("indexc not made", procName, 1);
goto Terminate;
}
if ((indexr = (int *)calloc(n, sizeof(int))) == NULL)
{
retValue = -4; // ERROR_INT("indexr not made", procName, 1);
goto Terminate;
}
if ((ipiv = (int *)calloc(n, sizeof(int))) == NULL)
{
retValue = -5; // ERROR_INT("ipiv not made", procName, 1);
goto Terminate;
}
for (i = 0; i < n; i++)
{
big = 0.0;
for (j = 0; j < n; j++)
{
if (ipiv[j] != 1)
{
for (k = 0; k < n; k++)
{
if (ipiv[k] == 0)
{
if (fabs(a[j][k]) >= big)
{
big = fabs(a[j][k]);
irow = j;
icol = k;
}
}
else if (ipiv[k] > 1)
{
retValue = -6; // ERROR_INT("singular matrix", procName, 1);
goto Terminate;
}
}
}
}
++(ipiv[icol]);
if (irow != icol)
{
for (l = 0; l < n; l++)
SWAP(a[irow][l], a[icol][l]);
SWAP(b[irow], b[icol]);
}
indexr[i] = irow;
indexc[i] = icol;
if (a[icol][icol] == 0.0)
{
retValue = -7; // ERROR_INT("singular matrix", procName, 1);
goto Terminate;
}
pivinv = 1.0 / a[icol][icol];
a[icol][icol] = 1.0;
for (l = 0; l < n; l++)
a[icol][l] *= pivinv;
b[icol] *= pivinv;
for (ll = 0; ll < n; ll++)
{
if (ll != icol)
{
dum = a[ll][icol];
a[ll][icol] = 0.0;
for (l = 0; l < n; l++)
a[ll][l] -= a[icol][l] * dum;
b[ll] -= b[icol] * dum;
}
}
}
for (l = n - 1; l >= 0; l--)
{
if (indexr[l] != indexc[l])
{
for (k = 0; k < n; k++)
SWAP(a[k][indexr[l]], a[k][indexc[l]]);
}
}
Terminate:
if (indexr)
free(indexr);
if (indexc)
free(indexc);
if (ipiv)
free(ipiv);
return retValue;
}
// --------------------------------------------------------------
// Map a source point to destination using projective transform
// --------------------------------------------------------------
// Params:
// sourcePoint: initial point
// destPoint: transformed point
// RetValue: 0: Success, !=0: Error
// --------------------------------------------------------------
// Notes:
// 1. You must call once computeCoeefficients() to compute
// the this->vc[] vector of 8 coefficients, before you call
// mapSourceToDestPoint().
// 2. If there was an error or the 8 coefficients were not computed,
// a -1 is returned and destPoint is just set to sourcePoint value.
// --------------------------------------------------------------
int genImageProjective::mapSourceToDestPoint(QPointF& sourcePoint, QPointF& destPoint)
{
if (coefficientsComputed)
{
float factor = 1.0f / (vc[6] * sourcePoint.x() + vc[7] * sourcePoint.y() + 1.);
destPoint.setX( factor * (vc[0] * sourcePoint.x() + vc[1] * sourcePoint.y() + vc[2]) );
destPoint.setY( factor * (vc[3] * sourcePoint.x() + vc[4] * sourcePoint.y() + vc[5]) );
return 0;
}
else // There was an error while computing coefficients
{
destPoint = sourcePoint; // just copy the source to destination...
return -1; // ...and return an error
}
}
//========================================
в то время как мой google-fu не смог произвести какое-либо твердое математическое решение, возможно, этот рисунок, который я нашел, может немного помочь.
http://studiochalkboard.evansville.edu/lp-diminish.html
Я думаю, что на самом деле может быть довольно сложно придумать правильную математику самостоятельно, это, вероятно, какое-то логарифмическое или суммирующее выражение. Надеюсь, рисунок и термины по этой ссылке могут предоставить что-то немного более доступное для поиска для тебя.
используя метод подразделения Бретона (который связан с методом расширения Монго), вы получите точную произвольную мощность двух делений. Чтобы разделить на не-мощность-двух делений с помощью этих методов, вам придется разделить на субпиксельный интервал, который может быть вычислительно дорогим.
тем не менее, я считаю, что вы можете применить вариант Теорема Хаги (который используется в оригами, чтобы разделить сторону на Nths, учитывая сторону, разделенную на (N-1)ths), чтобы перспективно-квадратные подразделения производить произвольные деления из ближайшей степени 2 без необходимости продолжать подразделять.
самым элегантным и быстрым решением было бы найти матрицу гомографии, которая отображает координаты прямоугольника в координаты фотографии.
с приличной библиотекой матриц это не должно быть сложной задачей, если вы знаете свою математику.
Ключевые Слова: Коллинеация, Гомография, Прямое Линейное Преобразование
однако рекурсивный алгоритм выше должен работать, но, вероятно, если ваши ресурсы ограничены, проективная геометрия-единственный способ идти.
в частном случае когда вы смотрите перпендикулярно сторонам 1 и 3, Вы можете разделить эти стороны на равные части. Затем нарисуйте диагональ и проведите параллели в сторону 1 через каждое пересечение диагонали и разделительных линий, нарисованных ранее.
это геометрическое решение, которое я придумал. Я не знаю, есть ли у "алгоритма" название.
скажем, вы хотите начать с деления "прямоугольника"на n частей с вертикальными линиями.
цель состоит в том, чтобы разместить точки P1..Pn-1 на верхней линии, которую мы можем использовать для рисования линий через них до точек, где левая и правая линии встречаются или параллельны им, когда такая точка не существует.
Если верхняя и нижняя линии параллельны друг другу просто поместите точки thoose, чтобы разделить верхнюю линию между углами равномерно.
остальное место n точек Q1..Qn на левой линии, так что верхний левый угол и верхний левый угол равноудалены, А I Qi ближе к верхнему левому углу, чем Qj. Чтобы отобразить Q-точки На верхнюю линию, найдите пересечение s линии от Qn через верхний правый угол и параллельную левую линию через пересечение верхней и нижней линии. Теперь соедините S с Q1..Qn-1. Этот пересечение новых линий с верхней линией-это разыскиваемые P-точки.
сделайте этот аналог для горизонтальных линий.
учитывая вращение вокруг оси Y, особенно если поверхности вращения, плоские, перспектива создается вертикальными градиентами. Они становятся все ближе в перспективе. Вместо использования диагоналей для определения четырех прямоугольников, которые могут работать с заданными степенями двух... определите два прямоугольника, левый и правый. Они будут выше ширины, в конце концов, если продолжать делить поверхность на более узкие вертикальные сегменты. Это может приспособить поверхности которые не квадратны. Если вращение вокруг оси x, тогда необходимы горизонтальные градиенты.
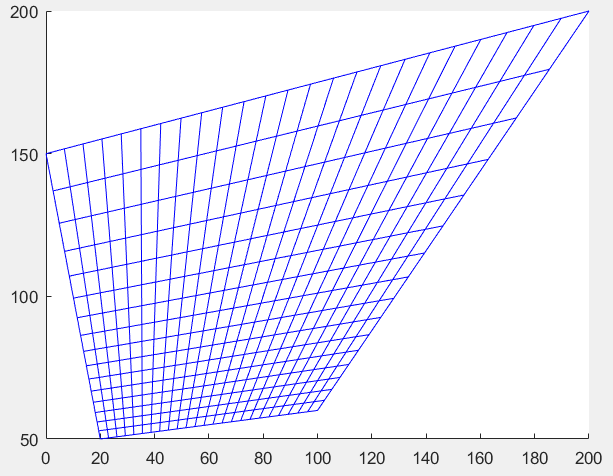
Я думаю, что выбранный ответ не является лучшим решением. Лучшее решение-применить перспективное (проективное) преобразование прямоугольника в простую сетку, как показано в сценарии Matlab и изображении. Вы также можете реализовать этот алгоритм с помощью C++ и OpenCV.
function drawpersgrid
sz = [ 24, 16 ]; % [x y]
srcpt = [ 0 0; sz(1) 0; 0 sz(2); sz(1) sz(2)];
destpt = [ 20 50; 100 60; 0 150; 200 200;];
% make rectangular grid
[X,Y] = meshgrid(0:sz(1),0:sz(2));
% find projective transform matching corner points
tform = maketform('projective',srcpt,destpt);
% apply the projective transform to the grid
[X1,Y1] = tformfwd(tform,X,Y);
hold on;
%% find grid
for i=1:sz(2)
for j=1:sz(1)
x = [ X1(i,j);X1(i,j+1);X1(i+1,j+1);X1(i+1,j);X1(i,j)];
y = [ Y1(i,j);Y1(i,j+1);Y1(i+1,j+1);Y1(i+1,j);Y1(i,j)];
plot(x,y,'b');
end
end
hold off;
проблема в том, что это преобразование из 3D в 2D, которое получает вас.
здесьС учебник о том, как это делается.
Что вам нужно сделать, это представить его в 3D (мир), а затем проецировать его до 2D (экран).
Это потребует от вас использовать матрицу преобразования 4D, которая делает проекцию на 4D однородной до 3D однородного вектора, который затем можно преобразовать в 2D пространственный вектор экрана.
Я не мог найти его в Google, но хорошие книги компьютерной графики будут иметь детали.
ключевые слова-проекционная матрица, проекция преобразование аффинного преобразования, однородные векторные, мировое пространство, пространство экрана, преобразование, 3D трансформации
и кстати, это обычно занимает несколько лекций, чтобы объяснить все это. Так что удачи.