Как найти центр кластера точек данных?
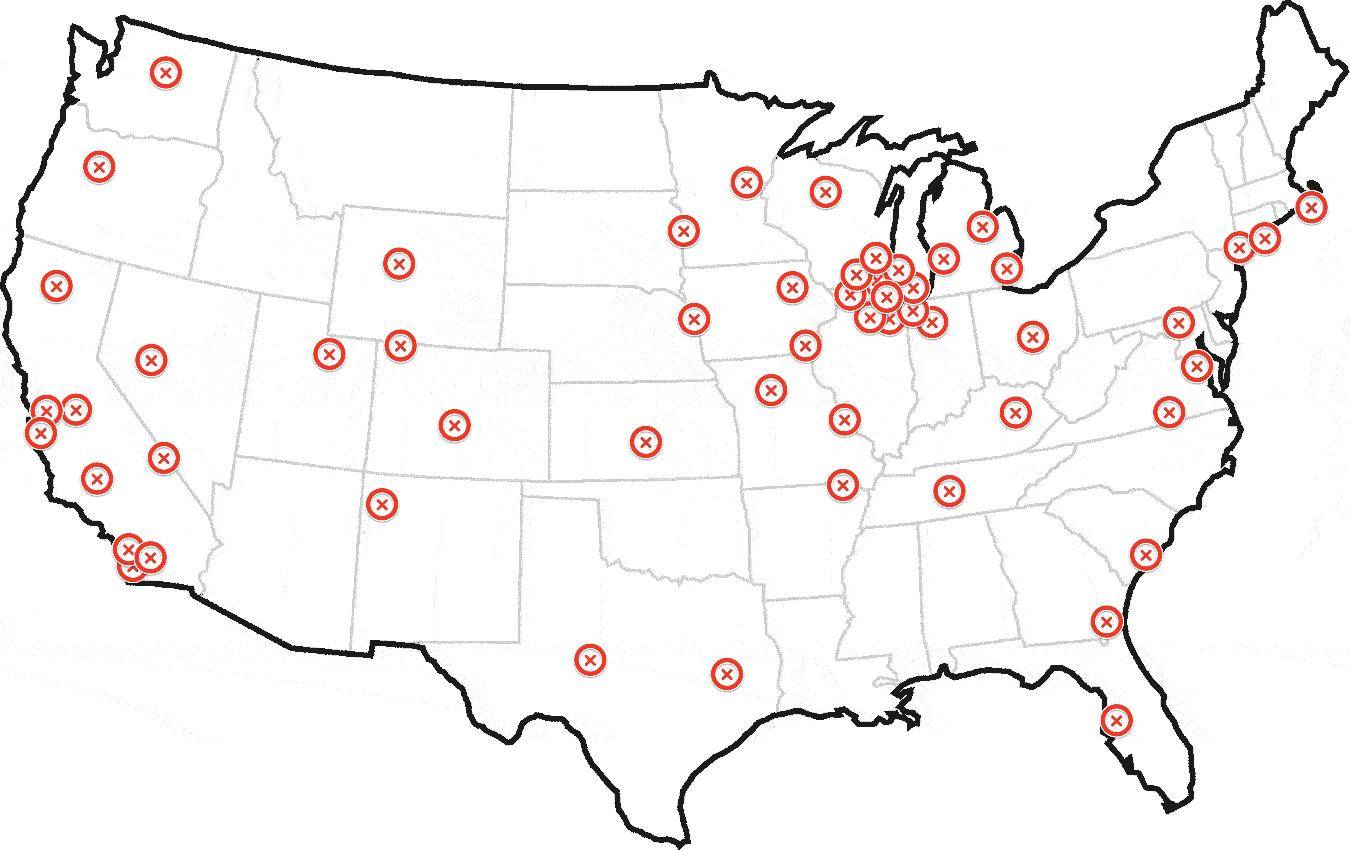
Как я могу найти тот же результат в коде?
Я ищу что-то вроде этого:
$geoCodeArray = array([GET=http://pastebin.com/grVsbgL9]);
function findHome($geoCodeArray) {
// magic
return $geoCode;
}
в конечном итоге генерируя что-то вроде это:
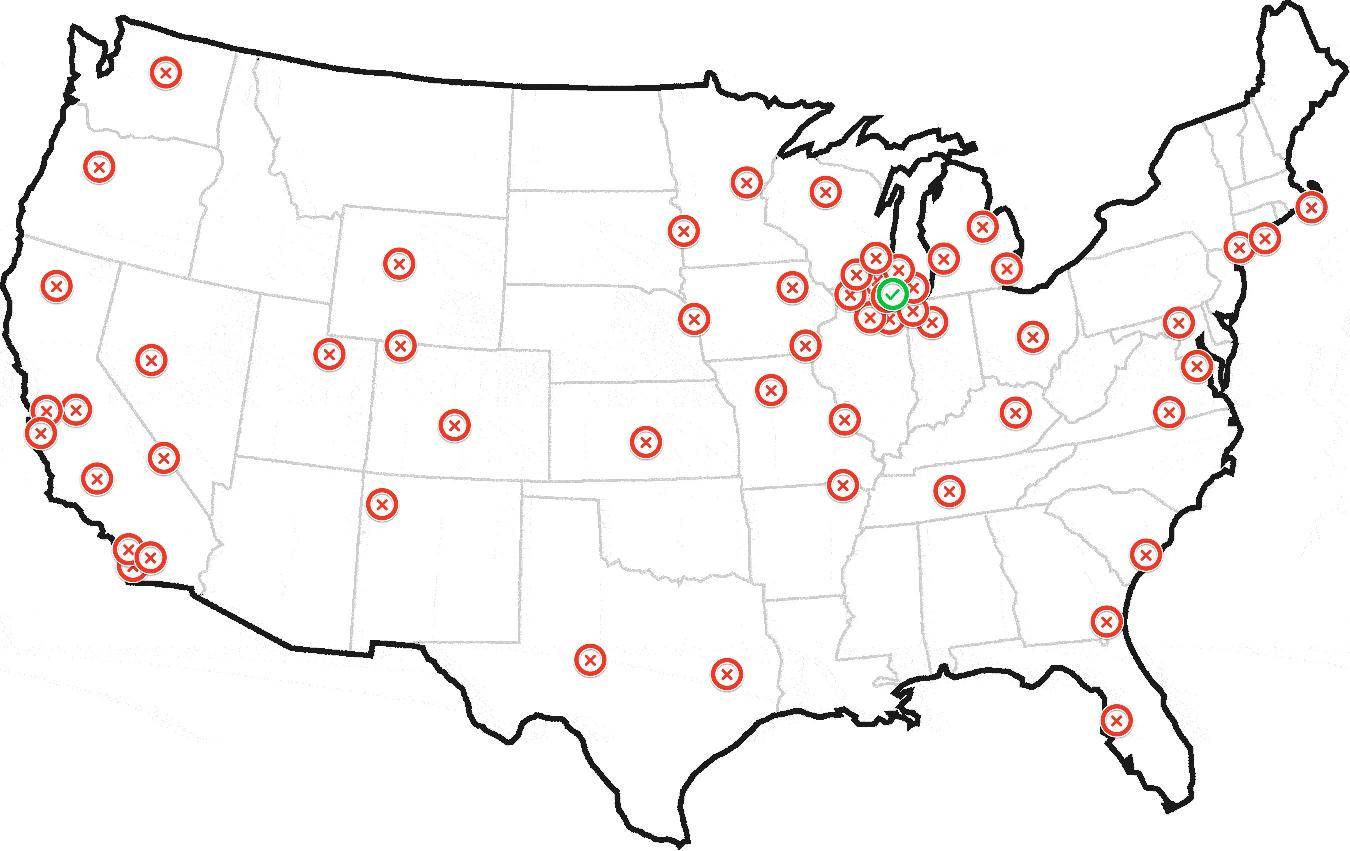
UPDATE: Sample Dataset
вот карта с образцом набора данных:http://batchgeo.com/map/c3676fe29985f00e1605cd4f86920179
вот пастебин 150 геокодов:http://pastebin.com/grVsbgL9
выше содержит 150 геокоды. Первые 50 находятся в нескольких кластерах недалеко от Чикаго. Остальные разбросаны по всей стране, включая небольшие кластеры в Нью-Йорке, Лос-Анджелесе и Сан-Франциско.
У меня есть около миллиона (серьезно) наборов данных, подобных этому, которые мне нужно будет перебрать и определить наиболее вероятный "дом". Ваша помощь очень ценится.
обновление 2: Самолет переключился на вертолет
14 ответов
следующие работы решение, даже если точки разбросаны по всей Земле, путем преобразования широты и долготы в прямоугольные координаты. Он выполняет своего рода KDE (оценку плотности ядра), но в первом проходе сумма ядер оценивается только в точках данных. Ядро должно быть выбрано в соответствии с проблемой. В приведенном ниже коде это то, что я мог бы в шутку / самонадеянно назвать Троссианом, т. е. 2-d2 / h2 для d≤h и h2 / d2 для d>h (где d-евклидово расстояние, а h - "полоса пропускания"$global_kernel_radius), но он также может быть гауссовым (e - d2 / 2h2), ядро Епанечникова (1-d2/h2 для d
по сути, каждая точка суммирует все точки, которые она имеет вокруг (включая себя), взвешивая их больше, если они ближе (по кривой колокола), а также взвешивание их по необязательному массиву веса $w_arr. Победителем считается очко с максимальной суммой. Как только победитель будет найден, "дом", который мы ищем, можно найти, повторив тот же процесс локально вокруг победителя (используя другую кривую колокола), или его можно оценить как "центр масс" всех точек в пределах заданного радиуса от победителя, где радиус может быть равен нулю.
алгоритм должен быть адаптирован к задаче путем выбора соответствующие ядра, выбирая, как уточнить поиск локально, и настраивая параметры. Для примера набора данных ядро Троссяна для первого прохода и ядро Епанечникова для второго прохода со всеми 3 радиусами, установленными на 30 mi, и шагом сетки 1 mi может быть хорошей отправной точкой, но только если два подкластера Чикаго следует рассматривать как один большой кластер. В противном случае необходимо выбрать меньшие радиусы.
function find_home($lat_arr, $lng_arr, $global_kernel_radius,
$local_kernel_radius,
$local_grid_radius, // 0 for no 2nd pass
$local_grid_step, // 0 for centroid
$units='mi',
$w_arr=null)
{
// for lat,lng <-> x,y,z see http://en.wikipedia.org/wiki/Geodetic_datum
// for K and h see http://en.wikipedia.org/wiki/Kernel_density_estimation
switch (strtolower($units)) {
/* */case 'nm' :
/*or*/case 'nmi': $m_divisor = 1852;
break;case 'mi': $m_divisor = 1609.344;
break;case 'km': $m_divisor = 1000;
break;case 'm': $m_divisor = 1;
break;default: return false;
}
$a = 6378137 / $m_divisor; // Earth semi-major axis (WGS84)
$e2 = 6.69437999014E-3; // First eccentricity squared (WGS84)
$lat_lng_count = count($lat_arr);
if ( !$w_arr) {
$w_arr = array_fill(0, $lat_lng_count, 1.0);
}
$x_arr = array();
$y_arr = array();
$z_arr = array();
$rad = M_PI / 180;
$one_e2 = 1 - $e2;
for ($i = 0; $i < $lat_lng_count; $i++) {
$lat = $lat_arr[$i];
$lng = $lng_arr[$i];
$sin_lat = sin($lat * $rad);
$sin_lng = sin($lng * $rad);
$cos_lat = cos($lat * $rad);
$cos_lng = cos($lng * $rad);
// height = 0 (!)
$N = $a / sqrt(1 - $e2 * $sin_lat * $sin_lat);
$x_arr[$i] = $N * $cos_lat * $cos_lng;
$y_arr[$i] = $N * $cos_lat * $sin_lng;
$z_arr[$i] = $N * $one_e2 * $sin_lat;
}
$h = $global_kernel_radius;
$h2 = $h * $h;
$max_K_sum = -1;
$max_K_sum_idx = -1;
for ($i = 0; $i < $lat_lng_count; $i++) {
$xi = $x_arr[$i];
$yi = $y_arr[$i];
$zi = $z_arr[$i];
$K_sum = 0;
for ($j = 0; $j < $lat_lng_count; $j++) {
$dx = $xi - $x_arr[$j];
$dy = $yi - $y_arr[$j];
$dz = $zi - $z_arr[$j];
$d2 = $dx * $dx + $dy * $dy + $dz * $dz;
$K_sum += $w_arr[$j] * ($d2 <= $h2 ? (2 - $d2 / $h2) : $h2 / $d2); // Trossian ;-)
// $K_sum += $w_arr[$j] * exp(-0.5 * $d2 / $h2); // Gaussian
}
if ($max_K_sum < $K_sum) {
$max_K_sum = $K_sum;
$max_K_sum_i = $i;
}
}
$winner_x = $x_arr [$max_K_sum_i];
$winner_y = $y_arr [$max_K_sum_i];
$winner_z = $z_arr [$max_K_sum_i];
$winner_lat = $lat_arr[$max_K_sum_i];
$winner_lng = $lng_arr[$max_K_sum_i];
$sin_winner_lat = sin($winner_lat * $rad);
$cos_winner_lat = cos($winner_lat * $rad);
$sin_winner_lng = sin($winner_lng * $rad);
$cos_winner_lng = cos($winner_lng * $rad);
$east_x = -$local_grid_step * $sin_winner_lng;
$east_y = $local_grid_step * $cos_winner_lng;
$east_z = 0;
$north_x = -$local_grid_step * $sin_winner_lat * $cos_winner_lng;
$north_y = -$local_grid_step * $sin_winner_lat * $sin_winner_lng;
$north_z = $local_grid_step * $cos_winner_lat;
if ($local_grid_radius > 0 && $local_grid_step > 0) {
$r = intval($local_grid_radius / $local_grid_step);
$r2 = $r * $r;
$h = $local_kernel_radius;
$h2 = $h * $h;
$max_L_sum = -1;
$max_L_sum_idx = -1;
for ($i = -$r; $i <= $r; $i++) {
$winner_east_x = $winner_x + $i * $east_x;
$winner_east_y = $winner_y + $i * $east_y;
$winner_east_z = $winner_z + $i * $east_z;
$j_max = intval(sqrt($r2 - $i * $i));
for ($j = -$j_max; $j <= $j_max; $j++) {
$x = $winner_east_x + $j * $north_x;
$y = $winner_east_y + $j * $north_y;
$z = $winner_east_z + $j * $north_z;
$L_sum = 0;
for ($k = 0; $k < $lat_lng_count; $k++) {
$dx = $x - $x_arr[$k];
$dy = $y - $y_arr[$k];
$dz = $z - $z_arr[$k];
$d2 = $dx * $dx + $dy * $dy + $dz * $dz;
if ($d2 < $h2) {
$L_sum += $w_arr[$k] * ($h2 - $d2); // Epanechnikov
}
}
if ($max_L_sum < $L_sum) {
$max_L_sum = $L_sum;
$max_L_sum_i = $i;
$max_L_sum_j = $j;
}
}
}
$x = $winner_x + $max_L_sum_i * $east_x + $max_L_sum_j * $north_x;
$y = $winner_y + $max_L_sum_i * $east_y + $max_L_sum_j * $north_y;
$z = $winner_z + $max_L_sum_i * $east_z + $max_L_sum_j * $north_z;
} else if ($local_grid_radius > 0) {
$r = $local_grid_radius;
$r2 = $r * $r;
$wx_sum = 0;
$wy_sum = 0;
$wz_sum = 0;
$w_sum = 0;
for ($k = 0; $k < $lat_lng_count; $k++) {
$xk = $x_arr[$k];
$yk = $y_arr[$k];
$zk = $z_arr[$k];
$dx = $winner_x - $xk;
$dy = $winner_y - $yk;
$dz = $winner_z - $zk;
$d2 = $dx * $dx + $dy * $dy + $dz * $dz;
if ($d2 <= $r2) {
$wk = $w_arr[$k];
$wx_sum += $wk * $xk;
$wy_sum += $wk * $yk;
$wz_sum += $wk * $zk;
$w_sum += $wk;
}
}
$x = $wx_sum / $w_sum;
$y = $wy_sum / $w_sum;
$z = $wz_sum / $w_sum;
$max_L_sum_i = false;
$max_L_sum_j = false;
} else {
return array($winner_lat, $winner_lng, $max_K_sum_i, false, false);
}
$deg = 180 / M_PI;
$a2 = $a * $a;
$e4 = $e2 * $e2;
$p = sqrt($x * $x + $y * $y);
$zeta = (1 - $e2) * $z * $z / $a2;
$rho = ($p * $p / $a2 + $zeta - $e4) / 6;
$rho3 = $rho * $rho * $rho;
$s = $e4 * $zeta * $p * $p / (4 * $a2);
$t = pow($s + $rho3 + sqrt($s * ($s + 2 * $rho3)), 1 / 3);
$u = $rho + $t + $rho * $rho / $t;
$v = sqrt($u * $u + $e4 * $zeta);
$w = $e2 * ($u + $v - $zeta) / (2 * $v);
$k = 1 + $e2 * (sqrt($u + $v + $w * $w) + $w) / ($u + $v);
$lat = atan($k * $z / $p) * $deg;
$lng = atan2($y, $x) * $deg;
return array($lat, $lng, $max_K_sum_i, $max_L_sum_i, $max_L_sum_j);
}
тот факт, что расстояния Евклида и не большой круг должен иметь незначительные последствия для поставленной задачи. Вычисление расстояний большого круга было бы гораздо более громоздким и привело бы только к тому, что вес очень далеких точек был бы значительно ниже - но эти точки уже имеют очень низкий вес. В принципе, тот же эффект может быть достигнут другим ядром. Ядра, которые имеют полное отсечение на некотором расстоянии, как ядро Епанечникова, вообще не имеют этой проблемы (на практике).
конверсия между lat, lng и x,y,z для данных WGS84 дается точно (хотя и без гарантии численной стабильности) больше как ссылка, чем из-за истинной необходимости. Если высота должна быть принята во внимание, или если требуется более быстрое обратное преобразование, обратитесь к статья в Википедии.
ядро Епанечникова, помимо того, что оно "более локально", чем ядра Гаусса и Тросса, имеет преимущество быть самым быстрым для второго цикла, который является O (ng), где g является числом точек локальной сетки, а также может использоваться в первом цикле, который является O (n2), если n большой.
Это можно решить, найдя угрозу поверхность. См.Rossmo это.
Это проблема хищника. Учитывая набор географически расположенных туш, где находится логово хищника? Формула Россмо решает эту проблему.
найти точку с оценка наибольшей плотности.
должно быть довольно просто. Используйте радиус ядра, который примерно покрывает большой аэропорт в диаметре. 2D ядро Гаусса или Епанечникова должно быть прекрасным.
http://en.wikipedia.org/wiki/Multivariate_kernel_density_estimation
это похоже на вычисление карты кучи:http://en.wikipedia.org/wiki/Heat_map а затем найти самое яркое пятно. Кроме вычисления яркости сразу.
для удовольствия я прочитал 1% образец Геокоординатов DBpedia (т. е. Wikipedia) В ELKI, проецировал его в 3D-пространство и включил наложение оценки плотности (скрытое в меню визуализаторов scatterplot). Вы можете видеть, что есть точка доступа в Европе, и в меньшей степени в США. Горячая точка в Европе-Польша, я полагаю. Последний раз, когда я проверял, кто-то, по-видимому, создал статью Википедии с Geocoordinates для практически любой город в Польше. Визуализатор ELKI, к сожалению, не позволяет увеличить, повернуть или уменьшить пропускную способность ядра, чтобы визуально найти самую плотную точку. Но это просто реализовать себя; вам, вероятно, также не нужно идти в 3D-пространство, но можно просто использовать широты и долготы.

оценка плотности ядра должна быть доступна в Т приложений. Тот, что в R, вероятно, намного мощнее. Я совсем недавно я обнаружил эту тепловую карту в ELKI, поэтому я знал, как быстро получить к ней доступ. См., например http://stat.ethz.ch/R-manual/R-devel/library/stats/html/density.html функции, связанные Р.
на ваших данных, в R, попробуйте, например:
library(kernSmooth)
smoothScatter(data, nbin=512, bandwidth=c(.25,.25))
это должно показать сильное предпочтение Чикаго.
library(kernSmooth)
dens=bkde2D(data, gridsize=c(512, 512), bandwidth=c(.25,.25))
contour(dens$x1, dens$x2, dens$fhat)
maxpos = which(dens$fhat == max(dens$fhat), arr.ind=TRUE)
c(dens$x1[maxpos[1]], dens$x2[maxpos[2]])
доходность [1] 42.14697 -88.09508, который находится менее чем в 10 км от аэропорта Чикаго.
чтобы получить лучшие координаты попробуйте:
- повторный запуск на 20x20 миль вокруг расчетных координат
- несвязанный KDE в этой области
- лучший выбор полосы пропускания с
dpik - более высокое разрешение сетки
в астрофизике мы используем так называемый"радиус половины массы". Учитывая распределение и его центр, радиус половины массы-это минимальный радиус круга, который содержит половину точек вашего распределения.
эта величина является характеристической длиной распределения точек.
Если вы хотите, чтобы дом вертолета, где точки максимально сосредоточены, так что это точка, которая имеет минимальный радиус половины массы!
мой алгоритм это выглядит следующим образом: для каждой точки вы вычисляете этот радиус половины массы, центрирующий распределение в текущей точке. "Домом" вертолета будет точка с минимальным радиусом в половину массы.
я реализовал его и вычисленный центр 42.149994 -88.133698 (который находится в Чикаго)
Я также использовал 0,2 от общей массы вместо 0,5 (половины), обычно используемых в астрофизике.
Это мой (в python) alghorithm, который находит дом вертолета:
import math
import numpy
def inside(points,center,radius):
ids=(((points[:,0]-center[0])**2.+(points[:,1]-center[1])**2.)<=radius**2.)
return points[ids]
points = numpy.loadtxt(open('points.txt'),comments='#')
npoints=len(points)
deltar=0.1
idcenter=None
halfrmin=None
for i in xrange(0,npoints):
center=points[i]
radius=0.
stayHere=True
while stayHere:
radius=radius+deltar
ninside=len(inside(points,center,radius))
#print 'point',i,'r',radius,'in',ninside,'center',center
if(ninside>=npoints*0.2):
if(halfrmin==None or radius<halfrmin):
halfrmin=radius
idcenter=i
print 'point',i,halfrmin,idcenter,points[idcenter]
stayHere=False
#print halfrmin,idcenter
print points[idcenter]
можно использовать DBSCAN для этой задачи.
DBSCAN-кластеризация на основе плотности с понятием шума. Вам нужно два параметра:
сначала количество точек кластера должно иметь минимум "minpoints".
И второй параметр окрестности называется "epsilon" это устанавливает порог расстояния до окружающих точек, которые должны быть включены в кластер.
весь алгоритм работает следующим образом:
- начать с произвольная точка в вашем наборе, которая еще не была посещена
- получить точки из Эпсилон окрестности отметить все, как посетил
- если вы нашли достаточно точек в этом районе (>параметр minpoints), вы запускаете новый кластер и назначаете эти точки. Теперь снова повторите шаг 2 для каждой точки в этом кластере.
- если у вас нет, объявите этот пункт как шум
- перейти все сначала, пока вы не посетили все точки
это очень просто реализовать, и есть много фреймворков, которые уже поддерживают этот алгоритм. Чтобы найти среднее значение вашего кластера, вы можете просто взять среднее значение всех назначенных точек из его окрестности.
однако, в отличие от метода, который предлагает @TylerDurden, это требует параметризации - поэтому вам нужно найти некоторые настроенные вручную параметры, которые соответствуют вашей проблеме.
в вашем случае вы можете попытаться установить minpoints в 10% от ваших общих очков, если самолет, вероятно, останется 10% времени, которое вы отслеживаете в аэропорту. Параметр плотности epsilon зависит от разрешения вашего географического датчика и метрики расстояния, которую вы используете - я бы предложил haversine расстояние для географических данных.
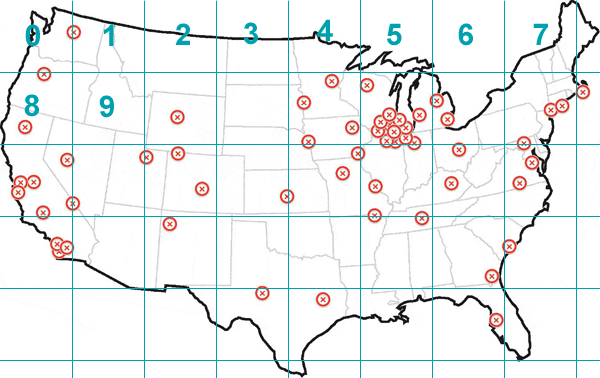
Как насчет разделить карту на зоны, а затем найти центр самолет в зону более плоской. Алгоритм будет что-то вроде этого
set Zones[40]
foreach Plane in Planes
Zones[GetZone(Plane.position)].Add(Plane)
set MaxZone = Zones[0]
foreach Zone in Zones
if MaxZone.Length() < Zone.Length()
MaxZone = Zone
set Center
foreach Plane in MaxZone
Center.X += Plane.X
Center.Y += Plane.Y
Center.X /= MaxZone.Length
Center.Y /= MaxZone.Length
все, что у меня есть на этой машине, - это старый компилятор, поэтому я сделал ASCII-версию этого. Он "рисует" (в ASCII) карту-точки-это точки, X - это реальный источник, G-это предполагаемый источник. Если пересекаются, только X показано.
примеры (сложность 1.5 и 3 соответственно):
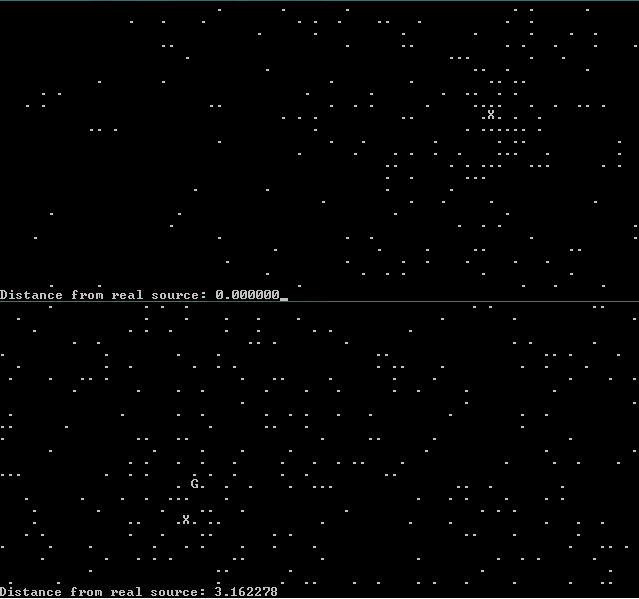
точки генерируются путем выбора случайной точки в качестве источника, а затем случайным образом распределяя точки, что делает их более вероятными ближе к источник.
DIFFICULTY является константой с плавающей запятой, которая регулирует начальную генерацию точки-насколько более вероятно, что точки будут ближе к источнику - если это 1 или меньше, программа должна быть в состоянии угадать точный источник или очень близко. В 2.5 он все равно должен быть довольно приличным. В 4+ он начнет догадываться хуже, но я думаю, что он все еще догадывается лучше, чем человек.
он может быть оптимизирован с помощью двоичного поиска по X, затем Y-это сделает думаю, хуже, но будет намного, намного быстрее. Или, начав с больших блоков, затем разделив лучший блок дальше (или лучший блок и 8 окружающих его). Для системы с более высоким разрешением один из них будет необходим. Это довольно наивный подход, хотя, но он, кажется, хорошо работает в системе 80x24. : D
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#define Y 24
#define X 80
#define DIFFICULTY 1 // Try different values...
static int point[Y][X];
double dist(int x1, int y1, int x2, int y2)
{
return sqrt((y1 - y2)*(y1 - y2) + (x1 - x2)*(x1 - x2));
}
main()
{
srand(time(0));
int y = rand()%Y;
int x = rand()%X;
// Generate points
for (int i = 0; i < Y; i++)
{
for (int j = 0; j < X; j++)
{
double u = DIFFICULTY * pow(dist(x, y, j, i), 1.0 / DIFFICULTY);
if ((int)u == 0)
u = 1;
point[i][j] = !(rand()%(int)u);
}
}
// Find best source
int maxX = -1;
int maxY = -1;
double maxScore = -1;
for (int cy = 0; cy < Y; cy++)
{
for (int cx = 0; cx < X; cx++)
{
double score = 0;
for (int i = 0; i < Y; i++)
{
for (int j = 0; j < X; j++)
{
if (point[i][j] == 1)
{
double d = dist(cx, cy, j, i);
if (d == 0)
d = 0.5;
score += 1000 / d;
}
}
}
if (score > maxScore || maxScore == -1)
{
maxScore = score;
maxX = cx;
maxY = cy;
}
}
}
// Print out results
for (int i = 0; i < Y; i++)
{
for (int j = 0; j < X; j++)
{
if (i == y && j == x)
printf("X");
else if (i == maxY && j == maxX)
printf("G");
else if (point[i][j] == 0)
printf(" ");
else if (point[i][j] == 1)
printf(".");
}
}
printf("Distance from real source: %f", dist(maxX, maxY, x, y));
scanf("%d", 0);
}
виртуальная Земля имеет очень хорошее объяснение того, каким образом вы можете сделать это относительно быстро. Они также привели примеры кода. Пожалуйста, взгляните на http://soulsolutions.com.au/Articles/ClusteringVirtualEarthPart1.aspx
простая модель смеси, похоже, работает довольно хорошо для этой проблемы.
В общем, чтобы получить точку, которая минимизирует расстояние до всех остальных точек в наборе данных, вы можете просто взять среднее. В этом случае требуется найти точку, минимизирующую расстояние от подмножества сосредоточенных точек. Если вы постулируете, что точка может исходить либо из концентрированного набора точек интереса, либо из диффузного набора фоновых точек, то это дает смесь модель.
Я включил некоторый код python ниже. Концентрированная область моделируется высокоточным нормальным распределением, а фоновая точка моделируется либо низкоточным нормальным распределением, либо равномерным распределением по ограничивающему прямоугольнику в наборе данных (существует строка кода, которая может быть прокомментирована для переключения между этими параметрами). Кроме того, модели смеси могут быть несколько нестабильными, поэтому запуск алгоритма EM несколько раз со случайными начальными условиями и выбор прогон с наибольшей логарифмической вероятностью дает лучшие результаты.
Если вы действительно смотрите на самолеты, то добавление какой-то временной динамики, вероятно, улучшит вашу способность сделать вывод о домашней базе.
Я бы также опасался формулы Россимо, потому что она включает некоторые довольно сильные предположения о распределении преступлений.
#the dataset
sdata='''41.892694,-87.670898
42.056048,-88.000488
41.941744,-88.000488
42.072361,-88.209229
42.091933,-87.982635
42.149994,-88.133698
42.171371,-88.286133
42.23241,-88.305359
42.196811,-88.099365
42.189689,-88.188629
42.17646,-88.173523
42.180531,-88.209229
42.18168,-88.187943
42.185496,-88.166656
42.170485,-88.150864
42.150634,-88.140564
42.156743,-88.123741
42.118555,-88.105545
42.121356,-88.112755
42.115499,-88.102112
42.119319,-88.112411
42.118046,-88.110695
42.117791,-88.109322
42.182189,-88.182449
42.194145,-88.183823
42.189057,-88.196182
42.186513,-88.200645
42.180917,-88.197899
42.178881,-88.192062
41.881656,-87.6297
41.875521,-87.6297
41.87872,-87.636566
41.872073,-87.62661
41.868239,-87.634506
41.86875,-87.624893
41.883065,-87.62352
41.881021,-87.619743
41.879998,-87.620087
41.8915,-87.633476
41.875163,-87.620773
41.879125,-87.62558
41.862763,-87.608757
41.858672,-87.607899
41.865192,-87.615795
41.87005,-87.62043
42.073061,-87.973022
42.317241,-88.187256
42.272546,-88.088379
42.244086,-87.890625
42.044512,-88.28064
39.754977,-86.154785
39.754977,-89.648437
41.043369,-85.12207
43.050074,-89.406738
43.082179,-87.912598
42.7281,-84.572754
39.974226,-83.056641
38.888093,-77.01416
39.923692,-75.168457
40.794318,-73.959961
40.877439,-73.146973
40.611086,-73.740234
40.627764,-73.234863
41.784881,-71.367187
42.371988,-70.993652
35.224587,-80.793457
36.753465,-76.069336
39.263361,-76.530762
25.737127,-80.222168
26.644083,-81.958008
30.50223,-87.275391
29.436309,-98.525391
30.217839,-97.844238
29.742023,-95.361328
31.500409,-97.163086
32.691688,-96.877441
32.691688,-97.404785
35.095754,-106.655273
33.425138,-112.104492
32.873244,-117.114258
33.973545,-118.256836
33.681497,-117.905273
33.622982,-117.734985
33.741828,-118.092041
33.64585,-117.861328
33.700707,-118.015137
33.801189,-118.251343
33.513132,-117.740479
32.777244,-117.235107
32.707939,-117.158203
32.703317,-117.268066
32.610821,-117.075806
34.419726,-119.701538
37.750358,-122.431641
37.50673,-122.387695
37.174817,-121.904297
37.157307,-122.321777
37.271492,-122.033386
37.435238,-122.217407
37.687794,-122.415161
37.542025,-122.299805
37.609506,-122.398682
37.544203,-122.0224
37.422151,-122.13501
37.395971,-122.080078
45.485651,-122.739258
47.719463,-122.255859
47.303913,-122.607422
45.176713,-122.167969
39.566,-104.985352
39.124201,-94.614258
35.454518,-97.426758
38.473482,-90.175781
45.021612,-93.251953
42.417881,-83.056641
41.371141,-81.782227
33.791132,-84.331055
30.252543,-90.439453
37.421248,-122.174835
37.47794,-122.181702
37.510628,-122.254486
37.56943,-122.346497
37.593373,-122.384949
37.620571,-122.489319
36.984249,-122.03064
36.553017,-121.893311
36.654442,-121.772461
36.482381,-121.876831
36.15042,-121.651611
36.274518,-121.838379
37.817717,-119.569702
39.31657,-120.140991
38.933041,-119.992676
39.13785,-119.778442
39.108019,-120.239868
38.586082,-121.503296
38.723354,-121.289062
37.878444,-119.437866
37.782994,-119.470825
37.973771,-119.685059
39.001377,-120.17395
40.709076,-73.948975
40.846346,-73.861084
40.780452,-73.959961
40.778829,-73.958931
40.78372,-73.966012
40.783688,-73.965325
40.783692,-73.965615
40.783675,-73.965741
40.783835,-73.965873
'''
import StringIO
import numpy as np
import re
import matplotlib.pyplot as plt
def lp(l):
return map(lambda m: float(m.group()),re.finditer('[^, \n]+',l))
data=np.array(map(lp,StringIO.StringIO(sdata)))
xmn=np.min(data[:,0])
xmx=np.max(data[:,0])
ymn=np.min(data[:,1])
ymx=np.max(data[:,1])
# area of the point set bounding box
area=(xmx-xmn)*(ymx-ymn)
M_ITER=100 #maximum number of iterations
THRESH=1e-10 # stopping threshold
def em(x):
print '\nSTART EM'
mlst=[]
mu0=np.mean( data , 0 ) # the sample mean of the data - use this as the mean of the low-precision gaussian
# the mean of the high-precision Gaussian - this is what we are looking for
mu=np.random.rand( 2 )*np.array([xmx-xmn,ymx-ymn])+np.array([xmn,ymn])
lam_lo=.001 # precision of the low-precision Gaussian
lam_hi=.1 # precision of the high-precision Gaussian
prz=np.random.rand( 1 ) # probability of choosing the high-precision Gaussian mixture component
for i in xrange(M_ITER):
mlst.append(mu[:])
l_hi=np.log(prz)+np.log(lam_hi)-.5*lam_hi*np.sum((x-mu)**2,1)
#low-precision normal background distribution
l_lo=np.log(1.0-prz)+np.log(lam_lo)-.5*lam_lo*np.sum((x-mu0)**2,1)
#uncomment for the uniform background distribution
#l_lo=np.log(1.0-prz)-np.log(area)
#expectation step
zs=1.0/(1.0+np.exp(l_lo-l_hi))
#compute bound on the likelihood
lh=np.sum(zs*l_hi+(1.0-zs)*l_lo)
print i,lh
#maximization step
mu=np.sum(zs[:,None]*x,0)/np.sum(zs) #mean
lam_hi=np.sum(zs)/np.sum(zs*.5*np.sum((x-mu)**2,1)) #precision
prz=1.0/(1.0+np.sum(1.0-zs)/np.sum(zs)) #mixure component probability
try:
if np.abs((lh-old_lh)/lh)<THRESH:
break
except:
pass
old_lh=lh
mlst.append(mu[:])
return lh,lam_hi,mlst
if __name__=='__main__':
#repeat the EM algorithm a number of times and get the run with the best log likelihood
mx_prm=em(data)
for i in xrange(4):
prm=em(data)
if prm[0]>mx_prm[0]:
mx_prm=prm
print prm[0]
print mx_prm[0]
lh,lam_hi,mlst=mx_prm
mu=mlst[-1]
print 'best loglikelihood:', lh
#print 'final precision value:', lam_hi
print 'point of interest:', mu
plt.plot(data[:,0],data[:,1],'.b')
for m in mlst:
plt.plot(m[0],m[1],'xr')
plt.show()
вы можете легко адаптировать формулу Россмо, цитируемую Тайлером Дерденом, к вашему случаю с помощью нескольких простых заметок:
по формуле :
эта формула дает что-то близкое к вероятности присутствия базовой операции для хищника или серийного убийцы. В вашем случае это может дать вероятность того, что база будет в определенной точке. Позже я объясню, как им пользоваться. Вы можете написать так :
Proba (база в точке A)= Sum{на всех пятнах} ( Phi/(dist^f)+(1-Phi) (B*(g-f)) / (2B-dist)^g )
использование евклидова расстояния
вам нужно евклидово расстояние, а не манхэттенское, потому что самолет или вертолет не привязан к дороге/улицам. Поэтому использование евклидова расстояния является правильным способом, если вы отслеживаете самолет , а не серийного убийцу. Таким образом, "dist" в Формуле-это евклидово расстояние между точечным тестированием ur и рассматриваемым пятном
принятие разумных переменная B
переменная B использовалась для представления правила "разумно умный убийца не убьет своего соседа". В вашем случае будет также применено, потому что никто не использует самолет/roflcopter, чтобы добраться до следующего угла улицы. мы можем предположить, что минимальное путешествие, например, 10 км или что-нибудь разумное, когда применяется к вашему случаю.
экспоненциальный коэффициент f
фактор f используется для добавления веса к расстоянию. Например, если все пятна находятся в небольшой области, вы можете захотеть большой фактор f, потому что вероятность аэропорта / базы / HQ будет быстро уменьшаться, если все ваши точки данных находятся в одном секторе. g работает аналогичным образом, позволяет выбрать размер области" база вряд ли будет рядом с пятном"
Фактор Phi:
снова этот фактор должен быть определен с использованием ваших знаний о проблеме. Оно позволяет выбрать самый точный фактор между "основанием близко к пятнам" и "я не буду использовать самолет, чтобы сделать 5 м", если, например, вы думаете, что второй почти не имеет значения, вы можете установить Phi в 0.95 (0<Phi<1) если оба интересны, phi будет около 0,5
как реализовать его как что-то полезное :
сначала вы хотите разделить карту на маленькие квадраты: сетка карты (так же ,как invisal) (чем меньше квадраты, тем точнее результат (в целом)), а затем с помощью формулы, чтобы найти более вероятное местоположение. На самом деле сетка-это просто массив со всеми возможными местоположениями. (если вы хотите быть точным, вы увеличиваете количество возможных пятен, но это потребует больше вычислительного времени, а PhP не известен своей удивительной скоростью)
:
//define all the factors you need(B , f , g , phi)
for(i=0..mesh_size) // computing the probability of presence for each square of the mesh
{
P(i)=0;
geocode squarePosition;//GeoCode of the square's center
for(j=0..geocodearray_size)//sum on all the known spots
{
dist=Distance(geocodearray[j],squarePosition);//small function returning distance between two geocodes
P(i)+=(Phi/pow(dist,f))+(1-Phi)*pow(B,g-f)/pow(2B-dist,g);
}
}
return geocode corresponding to max(P(i))
надеюсь, что это поможет вам
сначала я хотел бы выразить свою любовь к вашему методу в иллюстрации и объяснении проблемы ..
Если бы я был на вашем месте, я бы пошел на алгоритм на основе плотности как DBSCAN а потом ... --1-->после кластеризации областей и удаления точек шума несколько областей (вариантов) останутся .. тогда я ... --1-->возьмите кластер с наибольшей плотностью очков и рассчитать средняя точка и найти ближайшую реальную точку к нему . готово, нашел место! :).
с уважением,
Почему не что-то вроде этого:
- для каждой точки, вычислить расстояние от всех других точек и суммировать общую сумму.
- точка с наименьшей суммой - это ваш центр.
возможно, sum-не лучшая метрика для использования. Возможно, точка с самыми "маленькими расстояниями"?
суммировать расстояния. Возьмем точку с наименьшим суммированным расстоянием.
function () {
for i in points P:
S[i] = 0
for j in points P:
S[i] += distance(P[i], P[j])
return min(S);
}
вы можете взять минимальное остовное дерево и удалить самые длинные края. Меньшие деревья дают вам centeroid для поиска. Имя алгоритма-одноканальная K-кластеризация. Здесь есть сообщение: https://stats.stackexchange.com/questions/1475/visualization-software-for-clustering.
