Как найти максимальную сумму подпоследовательности с помощью динамического программирования?
я перечитываю руководство по разработке алгоритмов Скиены, чтобы наверстать упущенное со школы, и я немного озадачен его описаниями динамического программирования. Я просмотрел его в Википедии и на других сайтах, и хотя все описания имеют смысл, у меня возникли проблемы с выяснением конкретных проблем. В настоящее время я работаю над проблемой 3-5 из книги Skiena. (Дан массив из N действительных чисел, найти наибольшую сумму в течение любого непрерывного наращивает из вход.) У меня есть решение O(n^2), такое как описано в ответ. Но я застрял в решении O(N), используя динамическое программирование. Мне не ясно, каким должно быть отношение повторения.
Я вижу, что подпоследовательности образуют набор сумм, например:
S = {a,b,c, d}
a a+b a+b+c a+b+c+d
b b+c b+c+d
c c+d
d
чего я не понимаю, так это как выбрать, какой из них самый большой в линейном времени. Я пробовал делать такие вещи, как отслеживание наибольшую сумму, и если текущее значение положительное, добавьте его к сумме. Но когда у вас больше последовательностей, это становится проблематичным, потому что могут быть отрезки отрицательных чисел, которые уменьшат сумму, но позднее большое положительное число может вернуть ее к максимуму.
мне также напоминают суммированные таблицы областей. Вы можете вычислить все суммы, используя только кумулятивные суммы: a, a+b, a+b+c, a+b+c+d и т. д. (Например, если вам нужен b+c, это просто (a+b+c) - (a).) Но не вижу способа O(N) получить его.
может ли кто-нибудь объяснить мне, что такое решение динамического программирования O(N) для этой конкретной проблемы? Я чувствую, что почти понимаю, но что-то упускаю.
3 ответов
вы должны взгляните на этот pdf назад в школу в http://castle.eiu.edu Вот оно:

объяснение следующего псевдокода также int pdf.
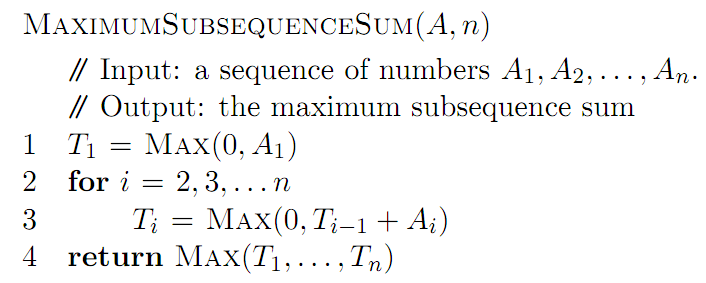
существует решение, например, сначала отсортировать массив в некоторой вспомогательной памяти, а затем применить самый длинный общий метод суб-последовательности к исходному массиву и отсортированному массиву, с суммой(не длиной) общей суб-последовательности в 2 массивах в качестве записи в таблицу (Memoization). Это также может решить проблему
Общее время работы-O (nlogn)+O (n^2) => O(n^2) Пространство равно O(n) + O(n^2) => O (n^2)
Это не хорошее решение, когда память входит в картину. Это просто чтобы дать представление о том, как проблемы могут быть сведены друг с другом.
мое понимание DP заключается в "создании таблицы". На самом деле, первоначальное значение "программирование" в DP-это просто создание таблиц.
ключ, чтобы выяснить,что положить в стол, или современные термины: какое состояние отслеживать, или что такое ключ/значение вершины в DAG (игнорируйте эти термины, если они звучат странно для вас).
Как выбрать dp[i] таблица, являющаяся самой большой суммой, заканчивающейся на index я массива, например, массива [5, 15, -30, 10]
второй важный ключ "оптимальная подструктура", то есть "считать" dp[i-1] уже хранит наибольшую сумму для суб-последовательностей, заканчивающихся на index i-1, вот почему единственный шаг на я решить, включать ли a[i] в под-последовательности или нет
dp[i] = max(dp[i-1], dp[i-1] + a[i])
первый термин max означает " не включать[i]", второй термин - "включать[i]". Обратите внимание, если мы не включаем a[i], в самая большая сумма пока остается dp[i-1], который исходит из аргумента "оптимальная подструктура".
таким образом, вся программа выглядит так (в Python):
a = [5,15,-30,10]
dp = [0]*len(a)
dp[0] = max(0,a[0]) # include a[0] or not
for i in range(1,len(a)):
dp[i] = max(dp[i-1], dp[i-1]+a[i]) # for sub-sequence, choose to add or not
print(dp, max(dp))
результат: наибольшая сумма суб-последовательности должна быть наибольшим элементом в dp стол, после i итерация по массиву a. Но посмотрите внимательно на dp, он содержит всю информацию.
так как он проходит только через элементы в array a один раз, Это O(n) алгоритм.
эта проблема кажется глупой, потому что пока a[i] положительно, мы всегда должны включать его в суб-последовательность, потому что это только увеличит сумму. Эта интуиция соответствует коду
dp[i] = max(dp[i-1], dp[i-1] + a[i])
Итак, Макс. сумма задачи суб-последовательности проста и не нуждается в DP вообще. Просто
sum = 0
for v in a:
if v >0
sum += v
однако, как насчет наибольшей суммы проблемы "непрерывного суб-массива". Все, что нам нужно изменить всего одну строку код
dp[i] = max(dp[i-1]+a[i], a[i])
первый член должен "включать[i] в непрерывный под-массив", второй член должен решить начать новый под-массив, начиная с[i].
в этом случае dp[i] - это Макс. sum непрерывный под-массив, заканчивающийся индексом-i.
это, конечно, лучше, чем наивный подход O(n^2)*O (n), к for j in range(0,i): внутри i-петли и sum все возможные суб-массивы.
один маленький нюанс, так как dp[0] установлен, если все предметы в a отрицательны, мы не будем выбирать. Поэтому для непрерывного под-массива max sum мы меняем это на
dp[0] = a[0]
