Как найти случайную точку в квадрате?
Я должен иметь возможность установить случайное местоположение для путевой точки для симулятора полета. Математика задача проста:
"чтобы найти одно случайное место в четырехугольнике, где есть равный шанс, что точка находится в любом месте."
визуально так:
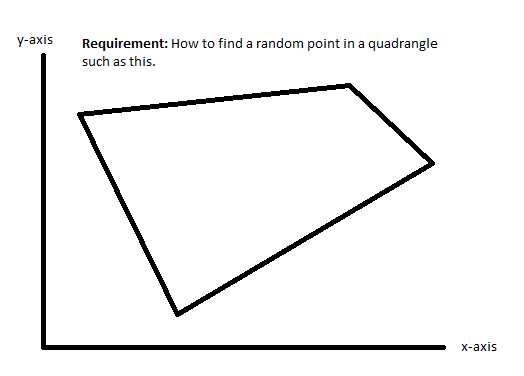
пример четырехугольника ABCD: A: [21417.78 37105.97] B: [38197.32 24009.74] C: [1364.19 2455.54] Д:[1227.77 37378.81]
спасибо заранее за любую помощь вы можете предоставить. :-)
изменить Спасибо всем за ваши ответы. Я взгляну на это в выходные и вручу принятый ответ тогда. Кстати, я должен был упомянуть, что четырехугольник может быть выпуклым или вогнутым. Сры насчет дат.
9 ответов
разделить четырехугольник на два треугольника, а затем использовать это отличный так ответ чтобы быстро найти случайную точку в одной из них.
обновление:
заимствования этого великого ссылке С Akusete при выборе случайной точки в треугольнике.
основная цифра http://mathworld.wolfram.com/images/eps-gif/TrianglePointPicking_700.gif
учитывая треугольник с одной вершиной на этот origin и остальные на позициях v1 и v2 выбери x http://mathworld.wolfram.com/images/equations/TrianglePointPicking/NumberedEquation2.gif где A1 и A2 однородны изменяется в интервале [0,1] , что дает точки, равномерно распределенные в четырехугольник (рисунок слева). Этот пункты не в интерьер треугольника затем можно либо отбросить, либо преобразованный в соответствующий точка внутри треугольника (справа рисунок.)
Я считаю, что есть два подходящих способа решить эту проблему.
первый, упомянутый другими плакатами, - найти наименьшую ограничивающую рамку, которая заключает прямоугольник, а затем генерировать точки в этом поле, пока вы не найдете точку, которая лежит внутри прямоугольника.
Find Bounding box (x,y,width, height)
Pick Random Point x1,y1 with ranges [x to x+width] and [y to y+height]
while (x1 or y1 is no inside the quadrangle){
Select new x1,y1
}
предполагая, что ваша площадь четырехугольника равна Q, а ограничивающий прямоугольник-A, вероятность того, что вам нужно будет создать N пар точек, равна 1 - (Q/A)^N, что приближается к 0 обратному экспоненциально.
Я бы рекомендовал выше подход, особенно в двух измерениях. Это очень быстро, чтобы генерировать очки и тест.
Если вы хотите, чтобы gaurentee завершения, то вы можете создать алгоритм только для генерации точек в четырехугольнике (легко), но вы должны убедиться, что распределение вероятностей точек даже thoughout четырехугольника.
http://mathworld.wolfram.com/TrianglePointPicking.html
дает очень хорошее explination
подход "грубой силы" - это просто цикл, пока у вас нет действительной координаты. В псевдокоде:
left = min(pa.x, pb.x, pc.x, pd.x)
right = max(pa.x, pb.x, pc.x, pd.x)
bottom = min(pa.y, pb.y, pc.y, pd.y)
top = max(pa.y, pb.y, pc.y, pd.y)
do {
x = left + fmod(rand, right-left)
y = bottom + fmod(rand, top-bottom)
} while (!isin(x, y, pa, pb, pc, pd));
вы можете использовать функцию запаса, вытащенную из сети для "isin". Я понимаю, что это не самая быстрая вещь в мире, но я думаю, что это сработает.
Итак, на этот раз решая, как выяснить, находится ли точка внутри квадрата:
четыре ребра могут быть выражены в виде линий в y = mx + b форма. Проверьте, находится ли точка выше или ниже каждой из четырех линий, и вместе вы можете выяснить, находится ли она внутри или снаружи.
вы можете просто несколько раз попробовать в любом месте прямоугольника, который ограничивает четырехугольник, пока вы не получите что-то внутри квадрата? Может быть, это даже быстрее, чем какой-то причудливый алгоритм, чтобы вы выбрали что-то внутри квадрата?
кстати, в этой постановке задачи, я думаю, что использование слова "найти" сбивает с толку. Вы не можете действительно найти случайное значение, удовлетворяющее условию; рандомизатор просто дает его вам. Что ты пытаешься do-это установить параметры на рандомизаторе, чтобы дать вам значения, соответствующие определенным критериям.
Я бы разделил ваш четырехугольник на несколько фигур, где каждая фигура представляет собой правильный многоугольник с одной стороной (или обеими сторонами), параллельной одной из осей. Например, для рисунка выше я бы сначала нашел максимальный прямоугольник, который помещается внутри четырехугольника, прямоугольник должен быть параллелен осям X/Y. Тогда в оставшуюся область я бы поместил треугольники, такие треугольники будут прилегать к каждой стороне прямоугольника.
тогда просто написать функция:
1) получить цифру наугад. 2) найти случайную точку на рисунке.
Если фигура, выбранная в #1, является прямоугольником, в ней должно быть довольно легко найти случайную точку. Хитрая часть состоит в том, чтобы написать процедуру, которая может найти случайную точку внутри треугольника
вы можете случайным образом создавать точки в bound-in-box только после того, как найдете тот, который находится внутри вашего многоугольника.
Так:
- найдите поле, содержащее все точки вашего многоугольника.
- создайте случайную точку внутри границ ранее найденного поля. Используйте случайные функции для генерации значений x и y.
- проверьте, находится ли эта точка внутри многоугольника (см. how здесь или здесь)
- если эта точка находится внутри полигональной остановки, вы сделали, если не перейти к Шагу 2
Так, это зависит от того, как вы хотите, чтобы ваши рассылки.
Если вы хотите, чтобы точки произвольно выбирались в вашем 2d-пространстве, то ответ Джейкоба велик. Если вы хотите, чтобы точки были похожи на перспективный вид (в вашем примере изображения больше плотности в правом верхнем углу, чем в левом нижнем), вы можете использовать билинейную интерполяцию.
билинейная интерполяция довольно легко. Сгенерировать два случайных числа s и t в диапазоне [0..1]. Затем, если ваши входные точки P0,p1,p2, p3 билинейная интерполяция:
bilerp(s,t) = t*(s*p3+(1-s)*p2) + (1-t)*(s*p1+(1-s)*p0)
основное различие заключается в том, хотите ли вы, чтобы ваше распределение было однородным в вашем 2d-пространстве (метод Якоба) или однородным в пространстве параметров.
Это интересная проблема, и, вероятно, есть действительно интересный ответ, но если вы просто хотите, чтобы он работал, позвольте мне предложить вам что-то простое.
вот алгоритм:
- выбрать случайные точки в пределах прямоугольника, ограничивающего четырехугольника.
- если он не находится внутри четырехугольника (или любой формы), повторите.
- профит!
редактировать
я обновил первый шаг, чтобы упомянуть ограничивающую коробку, по предложению Барта К.
