Как определить, находится ли 2D-точка внутри многоугольника?
Я пытаюсь создать быстро 2D точка внутри полигонального алгоритма, для использования в хит-тестировании (например,Polygon.contains(p:Point)). Были бы признательны за предложения относительно эффективных методов.
30 ответов
для графики я бы предпочел не целые числа. Многие системы используют целые числа для рисования пользовательского интерфейса (пиксели все-таки ints), но macOS, например, использует float для всего. macOS знает только точки, и точка может переводиться в один пиксель, но в зависимости от разрешения монитора она может переводиться на что-то другое. На экранах retina половина пункта (0.5/0.5) пиксел. Тем не менее, я никогда не замечал, что macOS UIs значительно медленнее, чем другие UIs. Ведь 3D API (OpenGL или Direct3D) тоже работает с поплавками и современными графическими библиотеками очень часто используют преимущества ускорения GPU.
теперь вы сказали, что скорость ваша главная забота, хорошо, давайте для скорости. Прежде чем запускать какой-либо сложный алгоритм, сначала выполните простой тест. Создайте ось выровнена ограничивающая коробка вокруг полигона. Это очень легко, быстро и уже может обеспечить вам много вычислений. Как это работает? Повторите все точки многоугольника и найдите минимальные / максимальные значения X и Y.
Е. Г. у вас есть очки (9/1), (4/3), (2/7), (8/2), (3/6). Это означает, что Xmin-2, Xmax-9, Ymin-1, а Ymax-7. Точка вне прямоугольника с двумя ребрами (2/1) и (9/7) не может находиться внутри многоугольника.
// p is your point, p.x is the x coord, p.y is the y coord
if (p.x < Xmin || p.x > Xmax || p.y < Ymin || p.y > Ymax) {
// Definitely not within the polygon!
}
это первый тест для любой точки. Как вы можете видеть, этот тест ультра быстрый, но он также очень грубый. Для обработки точек внутри прямоугольника, нам нужен более сложный алгоритм. Есть несколько способов, как это может быть рассчитанный. Какой метод работает также зависит от того, может ли многоугольник иметь отверстия или всегда будет сплошным. Вот примеры твердых (один выпуклый, один вогнутый):
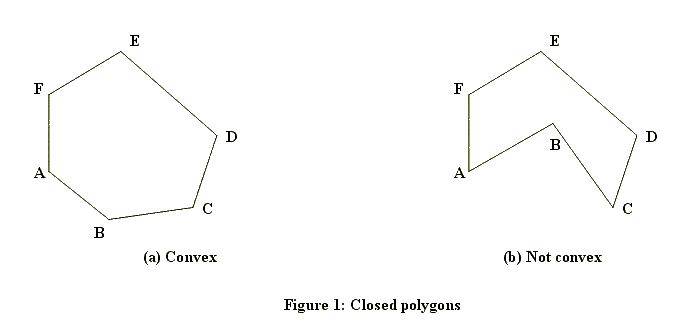
и вот один с дыркой:
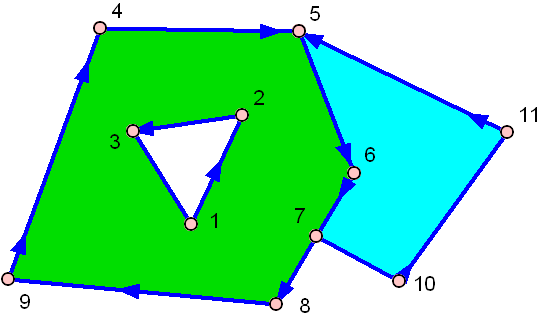
зеленый имеет отверстие в середине!
самый простой алгоритм, который может обрабатывать все три случая выше и по-прежнему довольно быстро называется рейкастинг. Идея алгоритм довольно прост: нарисуйте виртуальный Луч из любой точки за пределами полигона и подсчитайте, как часто он попадает в сторону полигона. Если количество четное, то снаружи многоугольника, если нечетное, то внутри.
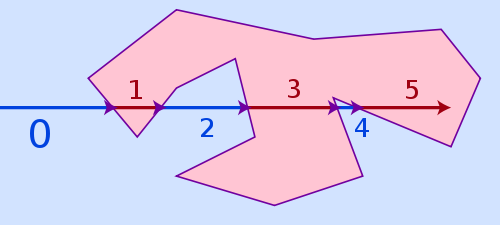
на алгоритм намотки номера было бы альтернативой, это более точно для точек, находящихся очень близко к полигональной линии, но это также намного медленнее. Ray casting может потерпеть неудачу для точек, слишком близких к a сторона полигона из-за ограниченной точности с плавающей запятой и округления, но на самом деле это едва ли проблема, как будто точка лежит так близко к стороне, часто визуально даже невозможно для зрителя распознать, находится ли она уже внутри или все еще снаружи.
у вас все еще есть ограничивающая коробка выше, помните? Просто выберите точку за пределами ограничительной рамки и используйте ее в качестве отправной точки для вашего луча. Е. Г. точки (Xmin - e/p.y) находится вне полигона наверняка.
но что такое e? Ну,e (на самом деле epsilon) дает ограничивающую рамку некоторые обивка. Как я уже сказал, трассировка лучей терпит неудачу, если мы начинаем слишком близко к полигональной линии. Поскольку ограничивающий прямоугольник может равняться многоугольнику (если многоугольник является прямоугольником, выровненным по оси, ограничивающий прямоугольник равен самому многоугольнику!), нам нужно немного подкладки, чтобы сделать это безопасным, вот и все. Как большой вы должны выбрать e? Не слишком большой. Это зависит от масштаба системы координат, которую вы используете для рисования. Если ширина шага пикселя равна 1.0, просто выберите 1.0 (но 0,1 также сработало бы)
теперь, когда у нас есть луч с его начальными и конечными координатами, проблема смещается от"является точкой внутри многоугольника "to"как часто луч пересекает сторону многоугольника". Поэтому мы не можем просто работать с полигональными точками, как раньше, теперь нам нужны фактические стороны. Сторона всегда определяется двумя точками.
side 1: (X1/Y1)-(X2/Y2)
side 2: (X2/Y2)-(X3/Y3)
side 3: (X3/Y3)-(X4/Y4)
:
вы нужно проверить Луч со всех сторон. Считайте луч вектором, а каждую сторону вектором. Луч должен попасть в каждую сторону ровно один раз или никогда. Он не может попасть в одну и ту же сторону дважды. Две линии в 2D пространстве всегда пересекаются ровно один раз, если они не параллельны, и в этом случае они никогда не пересекаются. Однако, поскольку векторы имеют ограниченную длину, два вектора могут не быть параллельными и никогда не пересекаться, потому что они слишком короткие, чтобы когда-либо встретиться друг с другом другой.
// Test the ray against all sides
int intersections = 0;
for (side = 0; side < numberOfSides; side++) {
// Test if current side intersects with ray.
// If yes, intersections++;
}
if ((intersections & 1) == 1) {
// Inside of polygon
} else {
// Outside of polygon
}
пока все хорошо, но как вы проверяете, пересекаются ли два вектора? Вот некоторый код C (не протестирован), который должен сделать трюк:
#define NO 0
#define YES 1
#define COLLINEAR 2
int areIntersecting(
float v1x1, float v1y1, float v1x2, float v1y2,
float v2x1, float v2y1, float v2x2, float v2y2
) {
float d1, d2;
float a1, a2, b1, b2, c1, c2;
// Convert vector 1 to a line (line 1) of infinite length.
// We want the line in linear equation standard form: A*x + B*y + C = 0
// See: http://en.wikipedia.org/wiki/Linear_equation
a1 = v1y2 - v1y1;
b1 = v1x1 - v1x2;
c1 = (v1x2 * v1y1) - (v1x1 * v1y2);
// Every point (x,y), that solves the equation above, is on the line,
// every point that does not solve it, is not. The equation will have a
// positive result if it is on one side of the line and a negative one
// if is on the other side of it. We insert (x1,y1) and (x2,y2) of vector
// 2 into the equation above.
d1 = (a1 * v2x1) + (b1 * v2y1) + c1;
d2 = (a1 * v2x2) + (b1 * v2y2) + c1;
// If d1 and d2 both have the same sign, they are both on the same side
// of our line 1 and in that case no intersection is possible. Careful,
// 0 is a special case, that's why we don't test ">=" and "<=",
// but "<" and ">".
if (d1 > 0 && d2 > 0) return NO;
if (d1 < 0 && d2 < 0) return NO;
// The fact that vector 2 intersected the infinite line 1 above doesn't
// mean it also intersects the vector 1. Vector 1 is only a subset of that
// infinite line 1, so it may have intersected that line before the vector
// started or after it ended. To know for sure, we have to repeat the
// the same test the other way round. We start by calculating the
// infinite line 2 in linear equation standard form.
a2 = v2y2 - v2y1;
b2 = v2x1 - v2x2;
c2 = (v2x2 * v2y1) - (v2x1 * v2y2);
// Calculate d1 and d2 again, this time using points of vector 1.
d1 = (a2 * v1x1) + (b2 * v1y1) + c2;
d2 = (a2 * v1x2) + (b2 * v1y2) + c2;
// Again, if both have the same sign (and neither one is 0),
// no intersection is possible.
if (d1 > 0 && d2 > 0) return NO;
if (d1 < 0 && d2 < 0) return NO;
// If we get here, only two possibilities are left. Either the two
// vectors intersect in exactly one point or they are collinear, which
// means they intersect in any number of points from zero to infinite.
if ((a1 * b2) - (a2 * b1) == 0.0f) return COLLINEAR;
// If they are not collinear, they must intersect in exactly one point.
return YES;
}
входные значения две конечные точки вектор 1 (v1x1/v1y1 и v1x2/v1y2) и вектор 2 (v2x1/v2y1 и v2x2/v2y2). Итак, у вас есть 2 вектора, 4 точки, 8 координат. YES и NO понятны. YES увеличивает перекрестках, NO ничего не делает.
что о КОЛЛИНЕАРНАЯ? Это означает, что оба вектора лежат на одной бесконечной линии, в зависимости от положения и длины, они не пересекаются вовсе, либо пересекаются в бесконечном количестве точек. Я не совсем уверен, как справиться с этим делом, я бы не считал его пересечением в любом случае. Ну, этот случай довольно редок на практике в любом случае из-за ошибок округления с плавающей запятой; лучший код, вероятно, не будет тестироваться для == 0.0f но вместо этого для чего-то вроде < epsilon, где epsilon-довольно маленький число.
Если вам нужно протестировать большее количество точек, вы можете немного ускорить все это, сохранив стандартные формы линейных уравнений сторон многоугольника в памяти, поэтому вам не нужно пересчитывать их каждый раз. Это сэкономит вам два умножения с плавающей запятой и три вычитания с плавающей запятой на каждом тесте в обмен на хранение трех значений с плавающей запятой на стороне полигона в памяти. Это типичная торговля временем памяти и вычислений выключено.
последнее, но не менее важное: если вы можете использовать 3D-оборудование для решения проблемы, есть интересная альтернатива. Просто позвольте GPU сделать всю работу за вас. Создайте поверхность рисования, которая находится вне экрана. Заполните его полностью черным цветом. Теперь позвольте OpenGL или Direct3D нарисовать ваш многоугольник(или даже все ваши многоугольники, если вы просто хотите проверить, находится ли точка внутри любого из них, но вам все равно, какой) и заполнить многоугольник (ы) другим цветом, например белым. Проверить если точка находится внутри многоугольника, получите цвет этой точки с поверхности чертежа. Это просто выборка памяти O(1).
конечно, этот метод можно использовать, только если ваша поверхность рисования не должна быть огромной. Если он не может поместиться в память GPU, этот метод медленнее, чем делать это на CPU. Если он должен быть огромным, и ваш GPU поддерживает современные шейдеры, вы все равно можете использовать GPU, реализуя приведенное выше приведение лучей в качестве шейдера GPU, что абсолютно возможно. Для большего количества полигонов или большого количества точек для тестирования это окупится, рассмотрим, что некоторые графические процессоры смогут тестировать от 64 до 256 точек параллельно. Обратите внимание, однако, что передача данных из CPU в GPU и обратно всегда стоит дорого, поэтому для простого тестирования нескольких точек против пары простых полигонов, где либо точки, либо полигоны являются динамическими и будут часто меняться, подход GPU редко окупается.
Я думаю, что следующий фрагмент кода является лучшим решением (взято из здесь):
int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy)
{
int i, j, c = 0;
for (i = 0, j = nvert-1; i < nvert; j = i++) {
if ( ((verty[i]>testy) != (verty[j]>testy)) &&
(testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )
c = !c;
}
return c;
}
Аргументы
- nvert: количество вершин в многоугольнике. Вопрос о том, повторять ли первую вершину в конце, обсуждался в вышеупомянутой статье.
- vertx, verty: массивы, содержащие х - и y-координаты вершин многоугольника.
- testx, testy: X-и y-координата контрольной точки.
он короткий и эффективный и работает как для выпуклых, так и для вогнутых полигонов. Как предлагалось ранее, сначала следует проверить ограничивающий прямоугольник и обработать полигональные отверстия отдельно.
идея довольно проста. Автор описывает его следующим образом:
Я запускаю полубесконечный луч горизонтально (увеличивая x, фиксированный y) из тестовой точки и считаю, сколько ребер он пересекает. На каждом пересекая, луч переключается между внутренним и внешним. Это называется теоремой кривой Джордана.
переменная c переключается с 0 на 1 и 1 на 0 каждый раз, когда горизонтальный луч пересекает любой край. Таким образом, в основном он отслеживает, четное или нечетное число пересеченных ребер. 0 означает четное, а 1 означает нечетное.
вот версияответ, данный nirg, который приезжает из этот профессор RPI. Обратите внимание, что использование кода из этого источника RPI требует атрибуции.
вверху добавлен флажок ограничивающего поля. Однако, как указывает Джеймс Браун, основной код почти так же быстр, как и сама проверка ограничительной рамки, поэтому проверка ограничительной рамки может фактически замедлить общую операцию, в случае, если большинство точек, которые вы проверяете, находятся внутри ограничивающий прямоугольник. Таким образом, вы можете оставить флажок ограничения, или альтернативой было бы предварительно вычислить ограничивающие поля ваших полигонов, если они не изменяют форму слишком часто.
public bool IsPointInPolygon( Point p, Point[] polygon )
{
double minX = polygon[ 0 ].X;
double maxX = polygon[ 0 ].X;
double minY = polygon[ 0 ].Y;
double maxY = polygon[ 0 ].Y;
for ( int i = 1 ; i < polygon.Length ; i++ )
{
Point q = polygon[ i ];
minX = Math.Min( q.X, minX );
maxX = Math.Max( q.X, maxX );
minY = Math.Min( q.Y, minY );
maxY = Math.Max( q.Y, maxY );
}
if ( p.X < minX || p.X > maxX || p.Y < minY || p.Y > maxY )
{
return false;
}
// http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html
bool inside = false;
for ( int i = 0, j = polygon.Length - 1 ; i < polygon.Length ; j = i++ )
{
if ( ( polygon[ i ].Y > p.Y ) != ( polygon[ j ].Y > p.Y ) &&
p.X < ( polygon[ j ].X - polygon[ i ].X ) * ( p.Y - polygon[ i ].Y ) / ( polygon[ j ].Y - polygon[ i ].Y ) + polygon[ i ].X )
{
inside = !inside;
}
}
return inside;
}
вот JavaScript-вариант ответа М. Каца, основанный на подходе Нирга:
function pointIsInPoly(p, polygon) {
var isInside = false;
var minX = polygon[0].x, maxX = polygon[0].x;
var minY = polygon[0].y, maxY = polygon[0].y;
for (var n = 1; n < polygon.length; n++) {
var q = polygon[n];
minX = Math.min(q.x, minX);
maxX = Math.max(q.x, maxX);
minY = Math.min(q.y, minY);
maxY = Math.max(q.y, maxY);
}
if (p.x < minX || p.x > maxX || p.y < minY || p.y > maxY) {
return false;
}
var i = 0, j = polygon.length - 1;
for (i, j; i < polygon.length; j = i++) {
if ( (polygon[i].y > p.y) != (polygon[j].y > p.y) &&
p.x < (polygon[j].x - polygon[i].x) * (p.y - polygon[i].y) / (polygon[j].y - polygon[i].y) + polygon[i].x ) {
isInside = !isInside;
}
}
return isInside;
}
вычислить ориентированную сумму углов между точкой p и каждой из вершин многоугольника. Если общий ориентированный угол составляет 360 градусов, точка находится внутри. Если сумма равна 0, точка находится снаружи.
Мне больше нравится этот метод, потому что он более надежный и менее зависит от численной точности.
методы, которые вычисляют равномерность числа пересечений, ограничены, потому что вы можете "ударить" вершину во время вычисления числа пересечения.
EDIT: Кстати, этот метод работает с вогнутыми и выпуклыми многоугольниками.
EDIT: недавно я нашел целый статья в Википедии по теме.
на статья Эрика Хейнса цитируется bobobobo действительно отлично. Особенно интересны таблицы, сравнивающие производительность алгоритмов; метод суммирования углов действительно плох по сравнению с другими. Также интересно, что оптимизации, такие как использование сетки поиска для дальнейшего разделения многоугольника на сектора "in" и "out", могут сделать тест невероятно быстрым даже на многоугольниках с > 1000 сторонами.
в любом случае, это первые дни, но мой голос идет к метод "пересечений", который в значительной степени описывает Меки, я думаю. Однако я нашел его наиболее кратко описано и кодифицировано Дэвидом Бурком. Мне нравится, что не требуется настоящая тригонометрия, и она работает для выпуклой и вогнутой, и она работает достаточно хорошо, поскольку количество сторон увеличивается.
кстати, вот одна из таблиц производительности из статьи Эрика Хейнса для интереса, тестирование на случайных полигонах.
number of edges per polygon
3 4 10 100 1000
MacMartin 2.9 3.2 5.9 50.6 485
Crossings 3.1 3.4 6.8 60.0 624
Triangle Fan+edge sort 1.1 1.8 6.5 77.6 787
Triangle Fan 1.2 2.1 7.3 85.4 865
Barycentric 2.1 3.8 13.8 160.7 1665
Angle Summation 56.2 70.4 153.6 1403.8 14693
Grid (100x100) 1.5 1.5 1.6 2.1 9.8
Grid (20x20) 1.7 1.7 1.9 5.7 42.2
Bins (100) 1.8 1.9 2.7 15.1 117
Bins (20) 2.1 2.2 3.7 26.3 278
этот вопрос настолько интересен. У меня есть еще одна работоспособная идея, отличная от других ответов этого поста.
идея состоит в том, чтобы использовать сумму углов, чтобы решить, находится ли цель внутри или снаружи. Если цель находится внутри области, сумма формы угла по цели и каждые две пограничные точки будет 360. Если цель находится снаружи, сумма не будет 360. Угол имеет направление. Если угол идет назад, то угол отрицательный. Это так же, как расчет кривой.
обратитесь к этому изображению, чтобы получить базовое понимание идеи:
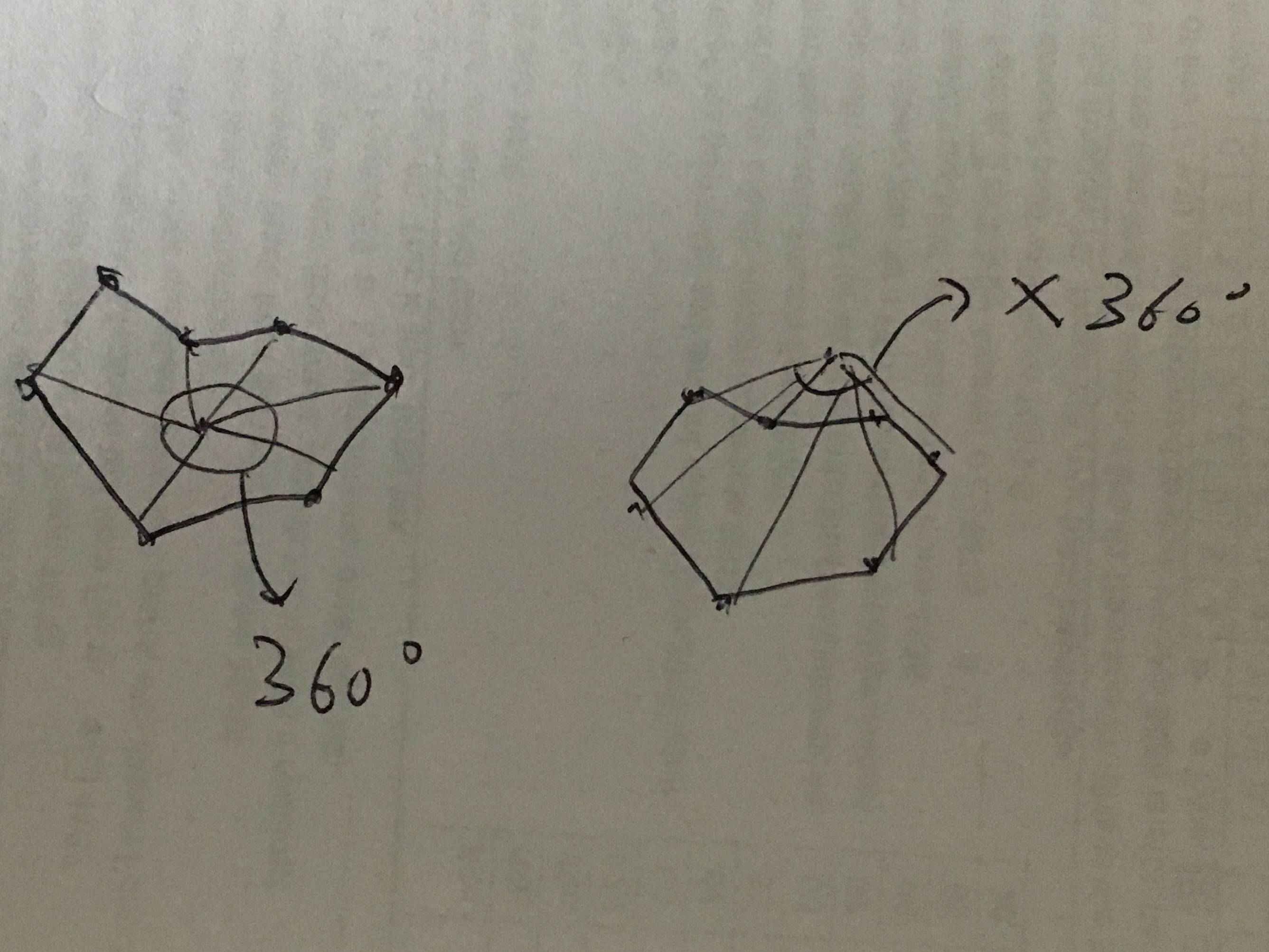
мой алгоритм предполагает, что по часовой стрелке является положительным направлением. Вот потенциальный вход:
[[-122.402015, 48.225216], [-117.032049, 48.999931], [-116.919132, 45.995175], [-124.079107, 46.267259], [-124.717175, 48.377557], [-122.92315, 47.047963], [-122.402015, 48.225216]]
ниже приведен код python, который реализует эту идею:
def isInside(self, border, target):
degree = 0
for i in range(len(border) - 1):
a = border[i]
b = border[i + 1]
# calculate distance of vector
A = getDistance(a[0], a[1], b[0], b[1]);
B = getDistance(target[0], target[1], a[0], a[1])
C = getDistance(target[0], target[1], b[0], b[1])
# calculate direction of vector
ta_x = a[0] - target[0]
ta_y = a[1] - target[1]
tb_x = b[0] - target[0]
tb_y = b[1] - target[1]
cross = tb_y * ta_x - tb_x * ta_y
clockwise = cross < 0
# calculate sum of angles
if(clockwise):
degree = degree + math.degrees(math.acos((B * B + C * C - A * A) / (2.0 * B * C)))
else:
degree = degree - math.degrees(math.acos((B * B + C * C - A * A) / (2.0 * B * C)))
if(abs(round(degree) - 360) <= 3):
return True
return False
очень нравится решение, опубликованное Nirg и отредактированное bobobobo. Я просто сделал его javascript дружественным и немного более разборчивым для моего использования:
function insidePoly(poly, pointx, pointy) {
var i, j;
var inside = false;
for (i = 0, j = poly.length - 1; i < poly.length; j = i++) {
if(((poly[i].y > pointy) != (poly[j].y > pointy)) && (pointx < (poly[j].x-poly[i].x) * (pointy-poly[i].y) / (poly[j].y-poly[i].y) + poly[i].x) ) inside = !inside;
}
return inside;
}
Swift версия ответ nirg:
extension CGPoint {
func isInsidePolygon(vertices: [CGPoint]) -> Bool {
guard !vertices.isEmpty else { return false }
var j = vertices.last!, c = false
for i in vertices {
let a = (i.y > y) != (j.y > y)
let b = (x < (j.x - i.x) * (y - i.y) / (j.y - i.y) + i.x)
if a && b { c = !c }
j = i
}
return c
}
}
ответ Дэвида Сегонда-это в значительной степени стандартный общий ответ, а Ричард Т-самая распространенная оптимизация, хотя есть и некоторые другие. Другие сильные оптимизации основаны на менее общих решениях. Например, если вы собираетесь проверить один и тот же многоугольник с большим количеством точек, триангуляция многоугольника может значительно ускорить процесс, поскольку существует ряд очень быстрых алгоритмов поиска TIN. Другой - если многоугольник и точки находятся на ограниченной плоскости с низким разрешением, скажем экранный дисплей, вы можете нарисовать многоугольник на буфер отображения памяти в заданном цвете и проверить цвет данного пикселя, чтобы увидеть, находится ли он в многоугольниках.
Как и многие оптимизации, они основаны на конкретных, а не общих случаях и дают преимущества, основанные на амортизированном времени, а не на одном использовании.
работая в этой области, я обнаружил, что вычислительная геометрия Джозефа О'Руркса в C 'ISBN 0-521-44034-3 является большой помощью.
тривиальным решением было бы разделить многоугольник на треугольники и проверить треугольники, как объяснено здесь
Если ваш полигон выпуклой возможно, есть лучший подход. Посмотрите на многоугольник как на набор бесконечных линий. Каждая линия делит пространство на две. для каждой точки легко сказать, находится ли она на той или иной стороне линии. Если точка находится на одной стороне всех линий, то она находится внутри многоугольника.
Я понимаю, что это старый, но вот алгоритм литья лучей, реализованный в Cocoa, если кто-то заинтересован. Не уверен, что это самый эффективный способ сделать что-то, но это может помочь кому-то.
- (BOOL)shape:(NSBezierPath *)path containsPoint:(NSPoint)point
{
NSBezierPath *currentPath = [path bezierPathByFlatteningPath];
BOOL result;
float aggregateX = 0; //I use these to calculate the centroid of the shape
float aggregateY = 0;
NSPoint firstPoint[1];
[currentPath elementAtIndex:0 associatedPoints:firstPoint];
float olderX = firstPoint[0].x;
float olderY = firstPoint[0].y;
NSPoint interPoint;
int noOfIntersections = 0;
for (int n = 0; n < [currentPath elementCount]; n++) {
NSPoint points[1];
[currentPath elementAtIndex:n associatedPoints:points];
aggregateX += points[0].x;
aggregateY += points[0].y;
}
for (int n = 0; n < [currentPath elementCount]; n++) {
NSPoint points[1];
[currentPath elementAtIndex:n associatedPoints:points];
//line equations in Ax + By = C form
float _A_FOO = (aggregateY/[currentPath elementCount]) - point.y;
float _B_FOO = point.x - (aggregateX/[currentPath elementCount]);
float _C_FOO = (_A_FOO * point.x) + (_B_FOO * point.y);
float _A_BAR = olderY - points[0].y;
float _B_BAR = points[0].x - olderX;
float _C_BAR = (_A_BAR * olderX) + (_B_BAR * olderY);
float det = (_A_FOO * _B_BAR) - (_A_BAR * _B_FOO);
if (det != 0) {
//intersection points with the edges
float xIntersectionPoint = ((_B_BAR * _C_FOO) - (_B_FOO * _C_BAR)) / det;
float yIntersectionPoint = ((_A_FOO * _C_BAR) - (_A_BAR * _C_FOO)) / det;
interPoint = NSMakePoint(xIntersectionPoint, yIntersectionPoint);
if (olderX <= points[0].x) {
//doesn't matter in which direction the ray goes, so I send it right-ward.
if ((interPoint.x >= olderX && interPoint.x <= points[0].x) && (interPoint.x > point.x)) {
noOfIntersections++;
}
} else {
if ((interPoint.x >= points[0].x && interPoint.x <= olderX) && (interPoint.x > point.x)) {
noOfIntersections++;
}
}
}
olderX = points[0].x;
olderY = points[0].y;
}
if (noOfIntersections % 2 == 0) {
result = FALSE;
} else {
result = TRUE;
}
return result;
}
Obj-C версия ответа nirg с методом выборки для точек тестирования. Ответ нирга хорошо сработал для меня.
- (BOOL)isPointInPolygon:(NSArray *)vertices point:(CGPoint)test {
NSUInteger nvert = [vertices count];
NSInteger i, j, c = 0;
CGPoint verti, vertj;
for (i = 0, j = nvert-1; i < nvert; j = i++) {
verti = [(NSValue *)[vertices objectAtIndex:i] CGPointValue];
vertj = [(NSValue *)[vertices objectAtIndex:j] CGPointValue];
if (( (verti.y > test.y) != (vertj.y > test.y) ) &&
( test.x < ( vertj.x - verti.x ) * ( test.y - verti.y ) / ( vertj.y - verti.y ) + verti.x) )
c = !c;
}
return (c ? YES : NO);
}
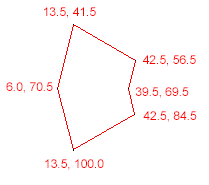
- (void)testPoint {
NSArray *polygonVertices = [NSArray arrayWithObjects:
[NSValue valueWithCGPoint:CGPointMake(13.5, 41.5)],
[NSValue valueWithCGPoint:CGPointMake(42.5, 56.5)],
[NSValue valueWithCGPoint:CGPointMake(39.5, 69.5)],
[NSValue valueWithCGPoint:CGPointMake(42.5, 84.5)],
[NSValue valueWithCGPoint:CGPointMake(13.5, 100.0)],
[NSValue valueWithCGPoint:CGPointMake(6.0, 70.5)],
nil
];
CGPoint tappedPoint = CGPointMake(23.0, 70.0);
if ([self isPointInPolygon:polygonVertices point:tappedPoint]) {
NSLog(@"YES");
} else {
NSLog(@"NO");
}
}
Я тоже думал, что 360 суммирование работает только для выпуклых полигонов, но это не так.
на этом сайте есть хорошая диаграмма, показывающая именно это, и хорошее объяснение при тестировании хитов: Gamasutra-врезаться в Новый год: обнаружение столкновений
C# версия ответа nirg здесь: я просто поделюсь кодом. Это может сэкономить кому-то время.
public static bool IsPointInPolygon(IList<Point> polygon, Point testPoint) {
bool result = false;
int j = polygon.Count() - 1;
for (int i = 0; i < polygon.Count(); i++) {
if (polygon[i].Y < testPoint.Y && polygon[j].Y >= testPoint.Y || polygon[j].Y < testPoint.Y && polygon[i].Y >= testPoint.Y) {
if (polygon[i].X + (testPoint.Y - polygon[i].Y) / (polygon[j].Y - polygon[i].Y) * (polygon[j].X - polygon[i].X) < testPoint.X) {
result = !result;
}
}
j = i;
}
return result;
}
Java Версия:
public class Geocode {
private float latitude;
private float longitude;
public Geocode() {
}
public Geocode(float latitude, float longitude) {
this.latitude = latitude;
this.longitude = longitude;
}
public float getLatitude() {
return latitude;
}
public void setLatitude(float latitude) {
this.latitude = latitude;
}
public float getLongitude() {
return longitude;
}
public void setLongitude(float longitude) {
this.longitude = longitude;
}
}
public class GeoPolygon {
private ArrayList<Geocode> points;
public GeoPolygon() {
this.points = new ArrayList<Geocode>();
}
public GeoPolygon(ArrayList<Geocode> points) {
this.points = points;
}
public GeoPolygon add(Geocode geo) {
points.add(geo);
return this;
}
public boolean inside(Geocode geo) {
int i, j;
boolean c = false;
for (i = 0, j = points.size() - 1; i < points.size(); j = i++) {
if (((points.get(i).getLongitude() > geo.getLongitude()) != (points.get(j).getLongitude() > geo.getLongitude())) &&
(geo.getLatitude() < (points.get(j).getLatitude() - points.get(i).getLatitude()) * (geo.getLongitude() - points.get(i).getLongitude()) / (points.get(j).getLongitude() - points.get(i).getLongitude()) + points.get(i).getLatitude()))
c = !c;
}
return c;
}
}
порт .Net:
static void Main(string[] args)
{
Console.Write("Hola");
List<double> vertx = new List<double>();
List<double> verty = new List<double>();
int i, j, c = 0;
vertx.Add(1);
vertx.Add(2);
vertx.Add(1);
vertx.Add(4);
vertx.Add(4);
vertx.Add(1);
verty.Add(1);
verty.Add(2);
verty.Add(4);
verty.Add(4);
verty.Add(1);
verty.Add(1);
int nvert = 6; //Vértices del poligono
double testx = 2;
double testy = 5;
for (i = 0, j = nvert - 1; i < nvert; j = i++)
{
if (((verty[i] > testy) != (verty[j] > testy)) &&
(testx < (vertx[j] - vertx[i]) * (testy - verty[i]) / (verty[j] - verty[i]) + vertx[i]))
c = 1;
}
}
рейкастинг:
на основе моделирования алгоритма простоты в http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html
некоторые вспомогательные предикаты:
exor(A,B):- \+A,B;A,\+B.
in_range(Coordinate,CA,CB) :- exor((CA>Coordinate),(CB>Coordinate)).
inside(false).
inside(_,[_|[]]).
inside(X:Y, [X1:Y1,X2:Y2|R]) :- in_range(Y,Y1,Y2), X > ( ((X2-X1)*(Y-Y1))/(Y2-Y1) + X1),toggle_ray, inside(X:Y, [X2:Y2|R]); inside(X:Y, [X2:Y2|R]).
get_line(_,_,[]).
get_line([XA:YA,XB:YB],[X1:Y1,X2:Y2|R]):- [XA:YA,XB:YB]=[X1:Y1,X2:Y2]; get_line([XA:YA,XB:YB],[X2:Y2|R]).
уравнение линии, заданной 2 точками A и B (Строка (A, B)):
(YB-YA)
Y - YA = ------- * (X - XA)
(XB-YB)
важно, чтобы направление вращения на линию установлен на часы-мудрый для границ и анти-часы-мудрый для отверстий. Мы собираемся проверить, является ли точка (X,Y) i.e испытанная точка находится слева полуплоскость нашей линии (это дело вкуса, это также может быть правая сторона, но также направление линий границ должно быть изменено в в этом случае), это проецировать Луч из точки вправо (или влево) и признать пересечение с линией. Мы выбрали проект Луч в горизонтальном направлении (опять же это дело вкуса, это также можно сделать по вертикали с аналогичными ограничениями), поэтому у нас есть:
(XB-XA)
X < ------- * (Y - YA) + XA
(YB-YA)
теперь нам нужно знать, находится ли точка слева (или справа) от только отрезок линии, а не вся плоскость, поэтому нам нужно ограничьте поиск только этим сегментом, но это легко, так как внутри сегмента только одна точка на линии может быть выше чем Y в вертикальная ось. Как это более сильное ограничение должен быть первым, чтобы проверить, поэтому мы принимаем только тех линий выполнение этого требования, а затем проверьте его возможность. У Иордана Теорема кривой любой луч, проецируемый на многоугольник, должен пересекаться на четное количество строк. Итак, мы закончили, мы бросим Луч в ... правильно, а затем каждый раз, когда он пересекает линию, переключайте ее состояние. Однако в нашей реализации мы собираемся проверить длину мешок решений, удовлетворяющих данному ограничения и решать innership на него. для каждой линии в полигоне это должно быть сделано.
is_left_half_plane(_,[],[],_).
is_left_half_plane(X:Y,[XA:YA,XB:YB], [[X1:Y1,X2:Y2]|R], Test) :- [XA:YA, XB:YB] = [X1:Y1, X2:Y2], call(Test, X , (((XB - XA) * (Y - YA)) / (YB - YA) + XA));
is_left_half_plane(X:Y, [XA:YA, XB:YB], R, Test).
in_y_range_at_poly(Y,[XA:YA,XB:YB],Polygon) :- get_line([XA:YA,XB:YB],Polygon), in_range(Y,YA,YB).
all_in_range(Coordinate,Polygon,Lines) :- aggregate(bag(Line), in_y_range_at_poly(Coordinate,Line,Polygon), Lines).
traverses_ray(X:Y, Lines, Count) :- aggregate(bag(Line), is_left_half_plane(X:Y, Line, Lines, <), IntersectingLines), length(IntersectingLines, Count).
% This is the entry point predicate
inside_poly(X:Y,Polygon,Answer) :- all_in_range(Y,Polygon,Lines), traverses_ray(X:Y, Lines, Count), (1 is mod(Count,2)->Answer=inside;Answer=outside).
ВЕРСИЯ VBA:
Примечание: помните, что если ваш многоугольник является областью на карте, что широта/долгота-это значения Y/X, а не X/Y (широта = Y, долгота = X) из-за того, что я понимаю, являются историческими последствиями с давних времен, когда долгота не была измерением.
модуль класса: CPoint
Private pXValue As Double
Private pYValue As Double
'''''X Value Property'''''
Public Property Get X() As Double
X = pXValue
End Property
Public Property Let X(Value As Double)
pXValue = Value
End Property
'''''Y Value Property'''''
Public Property Get Y() As Double
Y = pYValue
End Property
Public Property Let Y(Value As Double)
pYValue = Value
End Property
модуль:
Public Function isPointInPolygon(p As CPoint, polygon() As CPoint) As Boolean
Dim i As Integer
Dim j As Integer
Dim q As Object
Dim minX As Double
Dim maxX As Double
Dim minY As Double
Dim maxY As Double
minX = polygon(0).X
maxX = polygon(0).X
minY = polygon(0).Y
maxY = polygon(0).Y
For i = 1 To UBound(polygon)
Set q = polygon(i)
minX = vbMin(q.X, minX)
maxX = vbMax(q.X, maxX)
minY = vbMin(q.Y, minY)
maxY = vbMax(q.Y, maxY)
Next i
If p.X < minX Or p.X > maxX Or p.Y < minY Or p.Y > maxY Then
isPointInPolygon = False
Exit Function
End If
' SOURCE: http://www.ecse.rpi.edu/Homepages/wrf/Research/Short_Notes/pnpoly.html
isPointInPolygon = False
i = 0
j = UBound(polygon)
Do While i < UBound(polygon) + 1
If (polygon(i).Y > p.Y) Then
If (polygon(j).Y < p.Y) Then
If p.X < (polygon(j).X - polygon(i).X) * (p.Y - polygon(i).Y) / (polygon(j).Y - polygon(i).Y) + polygon(i).X Then
isPointInPolygon = True
Exit Function
End If
End If
ElseIf (polygon(i).Y < p.Y) Then
If (polygon(j).Y > p.Y) Then
If p.X < (polygon(j).X - polygon(i).X) * (p.Y - polygon(i).Y) / (polygon(j).Y - polygon(i).Y) + polygon(i).X Then
isPointInPolygon = True
Exit Function
End If
End If
End If
j = i
i = i + 1
Loop
End Function
Function vbMax(n1, n2) As Double
vbMax = IIf(n1 > n2, n1, n2)
End Function
Function vbMin(n1, n2) As Double
vbMin = IIf(n1 > n2, n2, n1)
End Function
Sub TestPointInPolygon()
Dim i As Integer
Dim InPolygon As Boolean
' MARKER Object
Dim p As CPoint
Set p = New CPoint
p.X = <ENTER X VALUE HERE>
p.Y = <ENTER Y VALUE HERE>
' POLYGON OBJECT
Dim polygon() As CPoint
ReDim polygon(<ENTER VALUE HERE>) 'Amount of vertices in polygon - 1
For i = 0 To <ENTER VALUE HERE> 'Same value as above
Set polygon(i) = New CPoint
polygon(i).X = <ASSIGN X VALUE HERE> 'Source a list of values that can be looped through
polgyon(i).Y = <ASSIGN Y VALUE HERE> 'Source a list of values that can be looped through
Next i
InPolygon = isPointInPolygon(p, polygon)
MsgBox InPolygon
End Sub
вот точка в полигональном тесте в C, которая не использует Ray-casting. И он может работать для перекрывающихся областей (перекрестков), см.
для обнаружения попадания на полигон нам нужно проверить две вещи:
- Если точка находится внутри полигона. (может быть выполнено алгоритмом Ray-Casting)
- Если точка находится на границе полигона(может быть выполнена тем же алгоритмом, который используется для обнаружения точки На полилинии (линии)).
для решения следующих особых случаев в трассировка лучей алгоритм:
- луч перекрывает одну из сторон многоугольника.
- точка находится внутри многоугольника, и луч проходит через вершину многоугольника.
- точка находится вне многоугольника, и луч просто касается одного из углов многоугольника.
Регистрация Определение Того, Находится Ли Точка Внутри Сложного Многоугольника. В статье приводится простой способ решить их, так что не будет никакого специального лечения, необходимого для вышеуказанных случаев.
вы можете сделать это, проверив, соответствует ли область, образованная соединением желаемой точки с вершинами вашего многоугольника, площади самого многоугольника.
или вы можете проверить, если сумма внутренних углов от вашей точки до каждой пары двух последовательных вершин многоугольника до вашей контрольной точки составляет 360, но у меня такое чувство, что первый вариант быстрее, потому что он не включает в себя деления или вычисления обратных тригонометрических функций.
I не знаю, что произойдет, если полигон имеет отверстие внутри него, но мне кажется, что основная идея может быть адаптирована к данной ситуации
вы также можете опубликовать вопрос в математическом сообществе. Бьюсь об заклад, у них есть миллион способов сделать это
Если вы ищете библиотеку java-скриптов, есть расширение javascript google maps v3 для класса Polygon, чтобы определить, находится ли в нем точка.
var polygon = new google.maps.Polygon([], "#000000", 1, 1, "#336699", 0.3);
var isWithinPolygon = polygon.containsLatLng(40, -90);
при использовании qt (Qt 4.3+), можно использовать функцию QPolygon containsPoint
ответ зависит от того, есть ли у вас простые или сложные полигоны. Простые полигоны не должны иметь пересечений отрезков линий. Поэтому они могут иметь отверстия, но линии не могут пересекать друг друга. Сложные области могут иметь пересечения линий - таким образом, они могут иметь перекрывающиеся области или области, которые касаются друг друга только одной точкой.
для простых полигонов лучшим алгоритмом является алгоритм литья лучей (число пересечений). Для сложных полигонов, этот алгоритм не обнаружение точек, находящихся внутри перекрывающихся областей. Поэтому для сложных полигонов, вы должны использовать алгоритм намотки количество.
вот отличная статья с реализацией обоих алгоритмов на языке C. Я пробовал их, и они хорошо работают.
Scala версия решения nirg (предполагает, что предварительная проверка ограничивающего прямоугольника выполняется отдельно):
def inside(p: Point, polygon: Array[Point], bounds: Bounds): Boolean = {
val length = polygon.length
@tailrec
def oddIntersections(i: Int, j: Int, tracker: Boolean): Boolean = {
if (i == length)
tracker
else {
val intersects = (polygon(i).y > p.y) != (polygon(j).y > p.y) && p.x < (polygon(j).x - polygon(i).x) * (p.y - polygon(i).y) / (polygon(j).y - polygon(i).y) + polygon(i).x
oddIntersections(i + 1, i, if (intersects) !tracker else tracker)
}
}
oddIntersections(0, length - 1, tracker = false)
}
Я сделал реализацию Python nirg это c++ код:
входы
- bounding_points: узлы, которые составляют многоугольник.
-
bounding_box_positions: кандидат указывает на фильтр. (В моей реализации, созданной из ограничивающей рамки.
(входные данные-это списки кортежей в формате:
[(xcord, ycord), ...])
возвращает
- все точки, которые находятся внутри многоугольника.
def polygon_ray_casting(self, bounding_points, bounding_box_positions):
# Arrays containing the x- and y-coordinates of the polygon's vertices.
vertx = [point[0] for point in bounding_points]
verty = [point[1] for point in bounding_points]
# Number of vertices in the polygon
nvert = len(bounding_points)
# Points that are inside
points_inside = []
# For every candidate position within the bounding box
for idx, pos in enumerate(bounding_box_positions):
testx, testy = (pos[0], pos[1])
c = 0
for i in range(0, nvert):
j = i - 1 if i != 0 else nvert - 1
if( ((verty[i] > testy ) != (verty[j] > testy)) and
(testx < (vertx[j] - vertx[i]) * (testy - verty[i]) / (verty[j] - verty[i]) + vertx[i]) ):
c += 1
# If odd, that means that we are inside the polygon
if c % 2 == 1:
points_inside.append(pos)
return points_inside
опять же, идея взята из здесь
Это работает только для выпуклых фигур, но уточнение портала Минковского и GJK также являются отличными вариантами для тестирования, если точка находится в многоугольнике. Вы используете вычитание Минковского для вычитания точки из многоугольника, а затем запускаете эти алгоритмы, чтобы увидеть, содержит ли многоугольник начало координат.
кроме того, интересно, что вы можете описать свои фигуры немного более неявно, используя функции поддержки, которые принимают вектор направления в качестве входного и выплевывают самую дальнюю точку вдоль этого вектора. Этот позволяет описать любую выпуклую форму.. изогнутый, сделанный из полигонов, или смешанный. Вы также можете выполнять операции по объединению результатов простых функций поддержки для создания более сложных фигур.
Подробнее: http://xenocollide.snethen.com/mpr2d.html
кроме того, game programming gems 7 рассказывает о том, как это сделать в 3d (:
