Как работает головоломка Инь-Ян?
Я пытаюсь понять семантику вызова / cc в схеме, а страница Википедии о продолжениях показывает головоломку инь-ян в качестве примера:
(let* ((yin
((lambda (cc) (display #@) cc) (call-with-current-continuation (lambda (c) c))))
(yang
((lambda (cc) (display #*) cc) (call-with-current-continuation (lambda (c) c)))) )
(yin yang))
нужно вывести @*@**@***@****@...,
но я не понимаю почему, я ожидал, что это выход @*@*********...
может кто-нибудь объяснить подробно, почему головоломка Инь-Ян работает так, как она работает?
6 ответов
Я не думаю, что понимаю это полностью, но я могу думать только об одном (очень рука-волнистые) объяснение для этого:
- первые @ и * печатаются, когда
yinиyangсначала связаны вlet*.(yin yang)применяется, и он возвращается наверх, сразу после завершения первого вызова/cc. - следующие @ и * печатаются, затем другой * печатается, потому что на этот раз через,
yinповторно привязывается к значению второй звонок / cc. -
(yin yang)применяется повторно, но на этот раз он выполняется в оригиналеyangв среду, гдеyinпривязан к первому вызову/cc, поэтому управление возвращается к печати другого @. Theyangаргумент содержит продолжение, которое было повторно захвачено на втором проходе, что, как мы уже видели, приведет к печати**. Итак, на этом третьем проходе,@*будет напечатано, тогда это продолжение двойн-звезд-печатания получает вызывается, поэтому он заканчивается 3 звездами, а затем это продолжение тройной звезды повторно захватывается ...
Понимание Схемы
я думаю, что по крайней мере половина проблемы с пониманием этой головоломки-это синтаксис схемы, с которым большинство не знакомы.
прежде всего, я лично нахожу call/cc x труднее понять, чем эквивалентную альтернативу,x get/cc. Это еще вызывает x, передавая ему текущее продолжение, но почему-то более поддается представлению в моей мозговой схеме.
имея это в виду, построить (call-with-current-continuation (lambda (c) c)) становится просто get-cc. Теперь мы дошли до этого:
(let* ((yin
((lambda (cc) (display #\@) cc) get-cc))
(yang
((lambda (cc) (display #\*) cc) get-cc)) )
(yin yang))
следующий шаг-это тело внутренней лямбды. (display #\@) cc в более привычный синтаксис (для меня, во всяком случае) означает print @; return cc;. Пока мы на нем, давайте также перепишем lambda (cc) body as function (arg) { body }, удалите кучу скобок и измените вызовы функций на синтаксис C-like, чтобы получить это:
(let* yin =
(function(arg) { print @; return arg; })(get-cc)
yang =
(function(arg) { print *; return arg; })(get-cc)
yin(yang))
теперь это начинает иметь больше смысла. Теперь это небольшой шаг, чтобы переписать это полностью в C-like синтаксис (или JavaScript-как, если хотите), чтобы получить это:
var yin, yang;
yin = (function(arg) { print @; return arg; })(get-cc);
yang = (function(arg) { print *; return arg; })(get-cc);
yin(yang);
самая трудная часть теперь закончена, мы расшифровали это из схемы! Просто шучу; это было трудно только потому, что у меня не было предыдущего опыта работы со схемой. Итак, давайте выясним, как это на самом деле работает.
основа для продолжения
обратите внимание на странно сформулированное ядро инь и Ян: оно определяет функцию и тут же называет его. Это выглядит так же, как (function(a,b) { return a+b; })(2, 3), который можно упростить до 5. Но упрощение вызовов внутри Инь / Ян было бы ошибкой, потому что мы не передаем ему обычное значение. Мы передаем функцию a продолжение.
продолжение-странный зверь на первый взгляд. Рассмотрим гораздо более простую программу:
var x = get-cc;
print x;
x(5);
изначально x устанавливается в текущий объект продолжения (bear with me), и print x выполняется, печатая что-то вроде <ContinuationObject>. Так пока все хорошо.
но продолжение подобно функции; его можно вызвать одним аргументом. Что он делает: возьмите аргумент, а затем прыжок туда, где было создано это продолжение, восстанавливая весь контекст и делая его таким, чтобы get-cc возвращает этот аргумент.
в нашем примере аргумент 5, поэтому мы по существу прыгаем прямо в середину этого var x = get-cc заявление, только на этот раз get-cc возвращает 5. Так что x становится 5, и следующий оператор переходит к печати 5. После этого мы пытаемся позвонить 5(5), что является ошибкой типа, и программа аварийно завершает работу.
обратите внимание, что вызов продолжения является прыжок, а не призыв. Он никогда не возвращается туда, где было вызвано продолжение. Это важно.
как работает программа
если вы следовали этому, то не надейтесь: эта часть действительно самая сложная. Вот наша программа снова, удаление объявлений переменных, потому что это псевдо-код в любом случае:
yin = (function(arg) { print @; return arg; })(get-cc);
yang = (function(arg) { print *; return arg; })(get-cc);
yin(yang);
при первом попадании строки 1 и 2 они просты: получить продолжение, вызвать функцию (arg), распечатать @, верните, сохраните это продолжение в yin. То же самое с yang. Теперь мы напечатали @*.
Далее, мы называем продолжение в yin, передав ему yang. Это заставляет нас перейти к строке 1, прямо внутри этого get-cc, и заставить его вернуться . Значение yang теперь передается в функцию, которая печатает @, а затем возвращает значение yang. Теперь yin назначается то продолжение, что yang есть. Далее переходим к строке 2: получаем c / c, печатаем *, хранить c / c в yang. Теперь у нас есть @*@*. И, наконец, переходим к третьей строке.
помните, что yin теперь имеет продолжение с момента первого выполнения строки 2. Поэтому мы переходим к строке 2, печатая секунду * и обновления yang. Теперь у нас есть @*@**. Наконец, вызовите yin продолжение снова, который будет прыгать в строку 1, печать @. И так далее. Честно говоря, в этот момент мой мозг выбрасывает исключение из памяти, и я теряю счет всему. Но, по крайней мере, мы добрались до @*@**!
это трудно понять и еще труднее объяснить, очевидно. Идеальный способ сделать это-пройти через него в отладчике, который может представлять продолжения, но, увы, я не знаю ни одного. Надеюсь, ты ... я наслаждался этим; конечно, наслаждался.
размышления во-первых, возможный ответ в конце.
я думаю, что код можно переписать следующим образом:
; call (yin yang)
(define (yy yin yang) (yin yang))
; run (call-yy) to set it off
(define (call-yy)
(yy
( (lambda (cc) (display #\@) cc) (call/cc (lambda (c) c)) )
( (lambda (cc) (display #\*) cc) (call/cc (lambda (c) c)) )
)
)
или с некоторыми дополнительными заявлениями дисплея, чтобы помочь увидеть, что происходит:
; create current continuation and tell us when you do
(define (ccc)
(display "call/cc=")
(call-with-current-continuation (lambda (c) (display c) (newline) c))
)
; call (yin yang)
(define (yy yin yang) (yin yang))
; run (call-yy) to set it off
(define (call-yy)
(yy
( (lambda (cc) (display "yin : ") (display #\@) (display cc) (newline) cc)
(ccc) )
( (lambda (cc) (display "yang : ") (display #\*) (display cc) (newline) cc)
(ccc) )
)
)
или такой:
(define (ccc2) (call/cc (lambda (c) c)) )
(define (call-yy2)
(
( (lambda (cc) (display #\@) cc) (ccc2) )
( (lambda (cc) (display #\*) cc) (ccc2) )
)
)
Ответ
это может быть неправильно, но я попробую.
я думаю, что ключевым моментом является то, что "называется" продолжение возвращает стек в некоторое предыдущее состояние-как будто ничего не произошло. Конечно, он не знает, что мы контролируем его, отображая @ и * символы.
мы изначально определили yin продолжение A что будет:
1. restore the stack to some previous point
2. display @
3. assign a continuation to yin
4. compute a continuation X, display * and assign X to yang
5. evaluate yin with the continuation value of yang - (yin yang)
но если мы называем yang продолжение, это происходит:
1. restore the stack to some point where yin was defined
2. display *
3. assign a continuation to yang
4. evaluate yin with the continuation value of yang - (yin yang)
начнем отсюда.
первый раз через вас сделать yin=A и yang=B as yin и yang время инициализации.
The output is @*
(как A и продолжения.)
теперь (yin yang) оценивается как (A B) впервые.
мы знаем, что A делает. Это:
1. restores the stack - back to the point where yin and yang were being initialised.
2. display @
3. assign a continuation to yin - this time, it is B, we don't compute it.
4. compute another continuation B', display * and assign B' to yang
The output is now @*@*
5. evaluate yin (B) with the continuation value of yang (B')
теперь (yin yang) оценивается как (B B').
мы знаем, что B делает. Это:
1. restore the stack - back to the point where yin was already initialised.
2. display *
3. assign a continuation to yang - this time, it is B'
The output is now @*@**
4. evaluate yin with the continuation value of yang (B')
так как стек был восстановлен до точки, где yin=A, (yin yang) оценивается как (A B').
мы знаем, что A делает. Это:
1. restores the stack - back to the point where yin and yang were being initialised.
2. display @
3. assign a continuation to yin - this time, it is B', we don't compute it.
4. compute another continuation B", display * and assign B" to yang
The output is now @*@**@*
5. evaluate yin (B') with the continuation value of yang (B")
мы знаем, что B' делает. Это:
1. restore the stack - back to the point where yin=B.
2. display *
3. assign a continuation to yang - this time, it is B"
The output is now @*@**@**
4. evaluate yin (B) with the continuation value of yang (B")
теперь (yin yang) оценивается как (B B").
мы знаем, что B делает. Это:
1. restore the stack - back to the point where yin=A and yang were being initialised.
2. display *
3. assign a continuation to yang - this time, it is B'"
The output is now @*@**@***
4. evaluate yin with the continuation value of yang (B'")
так как стек был восстановлен до точки, где yin=A, (yin yang) оценивается как (A B'").
.......
я думаю, у нас есть теперь узор.
каждый раз, когда мы называем (yin yang) мы петля через стопку B продолжения, пока мы не вернемся к тому, когда yin=A и @. Мы петля через стек B продолжение написания * каждый раз.
(я был бы очень рад, если бы это примерно так!)
Спасибо за вопрос.
Yinyang головоломка написана в схеме. Я предполагаю, что вы знаете основной синтаксис схемы.
но я предполагаю, что вы не знаете let* или call-with-current-continuation, я объясню эти два ключевых слова.
объяснить let*
если вы уже знаете, что, вы можете перейти к Explain call-with-current-continuation
let*, который выглядит как let, действует как let, но будет оценивать его определенные переменные ((yin ...) и (yang ...)) один за другим и с нетерпением. Что значит, он сначала оценит yin и yang.
вы можете прочитать больше здесь: использование Let in Scheme
объяснить call-with-current-continuation
если вы уже знаете, что, вы можете перейти к Yin-Yang puzzle.
это немного трудно объяснить call-with-current-continuation. Поэтому я использую метафору, чтобы объяснить это.
изображение волшебника, который знал заклинание, которое было call-with-current-continuation. Как только он произнесет заклинание, он создаст новое. Вселенная, и отправить его-себя к ней. Но он мог! .. --215-->ничего в новой вселенной, но ждет, когда кто-то назовет его имя. После называют, волшебник вернется в исходную вселенную, имея бедного парня - "кого-то" - в руке, и продолжит свою волшебную жизнь. Если не был вызван, когда новая вселенная закончилась, мастер также вернулся в исходную вселенную.
Хорошо, давайте будем более техническими.
call-with-current-continuation функция которые принимают функцию как параметр. Как только вы позвоните call-with-current-continuation С функцией F, он упакует текущую рабочую среду, которая называется current-continuation в качестве параметра C, и отправьте его в функцию F, и выполнить F. Таким образом, вся программа становится (F C). Или быть более JavaScript:F(C);. C действует как функция. Если C не вызывается F, тогда это обычная программа, когда F возвращает call-with-current-continuation имеет значение Fвозврата значение. Но если ... --46--> вызывается с параметром V, это снова изменит всю программу. Программа возвращается к государство, когда call-with-current-continuation называют. Но теперь ... --28--> возвращает значение, которое V. И программа продолжается.
возьмем пример.
(define (f return)
(return 2)
3)
(display (f whatever)) ;; 3
(display (call-with-current-continuation f)) ;; 2
(display (call-with-current-continuation (lambda (x) 4))) ;; 4
первый display выход 3, причины.
, а второй display выход 2. Почему?
давайте погрузимся в он.
при оценке (display (call-with-current-continuation f)), он сначала оценивает (call-with-current-continuation f). Мы знаем, что это изменит всю программу на
(f C)
учитывая определение для f, она имеет (return 2). Мы должны оценить (C 2). Вот когда continuation называют. Поэтому измените всю программу на
(display (call-with-current-continuation f))
но сейчас...call-with-current-continuation имеет значение 2. Так программа становится:
(display 2)
Инь-Ян головоломка
давайте посмотрим на головоломку.
(let* ((yin
((lambda (cc) (display #\@) cc) (call-with-current-continuation (lambda (c) c))))
(yang
((lambda (cc) (display #\*) cc) (call-with-current-continuation (lambda (c) c)))))
(yin yang))
давайте сделаем его более читабельным.
(define (id c) c)
(define (f cc) (display #\@) cc)
(define (g cc) (display #\*) cc)
(let* ((yin
(f (call-with-current-continuation id)))
(yang
(g (call-with-current-continuation id))))
(yin yang))
давайте запустим программу в нашем мозгу.
круглый 0
let* заставить нас оценить yin первый. yin is
(f (call-with-current-continuation id))
Итак, мы оцениваем (call-with-current-continuation id) первый. Он упаковывает текущую среду, которую мы называем C_0 отличить с другим продолжением в линии времени, и оно входит в совершенно новое Вселенная: id. Но!--79--> просто возвращает C_0.
мы должны помнить, что C_0 есть. C_0 это такая программа:
(let* ((yin
(f ###))
(yang
(g (call-with-current-continuation id))))
(yin yang))
### является заполнителем, который в будущем будет заполняться значением, которое C_0 забирает.
но id просто возвращает C_0. Он не зовет C_0. Если он позовет, мы войдем 'ы. Но этого не произошло, поэтому мы продолжаем оценивать yin.
(f C_0) ;; yields C_0
f - это функция, как id, но он имеет побочный эффект -- вывод @.
Итак, вывод программы @ и пусть yin на C_0. Теперь программа становится
(let* ((yin C_0)
(yang
(g (call-with-current-continuation id))))
(yin yang))
после yin оценено, мы начинаем оценивать yang. yang is
(g (call-with-current-continuation id))
call-with-current-continuation здесь создайте еще одно продолжение, названное C_1. C_1 is:
(let* ((yin C_0)
(yang
(g ###)))
(yin yang))
### это заполнитель. Обратите внимание, что в этом продолжении, yinопределяется значение (вот что let* do). Мы уверены, что - это C_0 здесь.
с (id C_1) is C_1, so - это
(g C_1)
g имеет побочный эффект -- outputting *. Так делает программа.
теперь C_1.
к настоящему времени мы показали @*
так что теперь становится:
(let* ((yin C_0)
(yang C_1))
(yin yang))
как yin и yang решены, мы должны оценить (yin yang). Это
(C_0 C_1)
Святой SH*Т!
но, наконец, C_0 называется. Итак, мы летим в C_0 Вселенная и забыть все об этих sh * ts. Мы никогда больше не вернемся в эту вселенную.
раунд 1
C_0 возьмите с C_1 обратно. Программа теперь становится(если вы забыли, что C_0 расшифровывается, вернуться чтобы увидеть его):
(let* ((yin
(f C_1))
(yang
(g (call-with-current-continuation id))))
(yin yang))
Ах, мы находим, что yinзначение еще не определено. Поэтому мы оцениваем его. В процессе оценки yin, мы выводим @ as fпобочный эффект. И мы знаем!--36-- > is C_1 сейчас.
начинаем оценивать yang и call-with-current-continuation снова. Мы практикуемся. Создаем продолжение C_2 что означает:
(let* ((yin C_1)
(yang
(g ###)))
(yin yang))
и мы показываем * as g выполнения. И мы идем сюда
(let* ((yin C_1)
(yang C_2))
(yin yang))
Итак, мы получили:
(C_1 C_2)
ты знаешь, куда мы идем. Мы собираемся 'ы. Мы вспоминаем его из памяти (или копируем и вставляем с веб-страницы). Теперь:
(let* ((yin C_0)
(yang
(g C_2)))
(yin yang))
мы знаем, что в C_1с Вселенной, yin's значение было определено. Итак, мы начинаем оценивать yang. Поскольку мы практикуемся, я прямо скажу вам, что он отображает * и будет:
(C_0 C_2)
теперь у нас есть напечатано @*@**, и мы собираемся C_0Вселенная берет с C_2.
Раунд 2
как мы практикуемся, я скажу вам, что мы показываем'@',yin is C_2, и мы создаем новое продолжение C_3, что означает:
(let* ((yin C_2)
(yang
(g ###)))
(yin yang))
и *, yang is C_3, и он становится
(C_2 C_3)
и мы можем продолжить. Но я остановлюсь здесь, я показал вам, что такое головоломка Инь-Ян первые несколько выходов.
почему количество * увеличивается?
теперь ваша голова полна деталей. Я сделаю для вас резюме.
я буду использовать синтаксис Haskell как для упрощения. И cc сокращенно call-with-current-continuation.
, когда #C_i# отмечается #, это означает, что продолжение создается здесь. ; средства производства
yin = f cc id
yang = g cc id
yin yang
---
yin = f #C_0# ; @
yang = g cc id
yin yang
---
yin = C_0
yang = g #C_1# ; *
yin yang
---
C_0 C_1
---
yin = f C_1 ; @
yang = g #C_2# ; *
yin yang
---
C_1 C_2
---
yin = C_0
yang = g C_2 ; *
yin yang
---
C_0 C_2
---
yin = f C_2 ; @
yang = g #C_3#; *
yin yang
---
C_2 C_3
---
yin = C_1
yang = g C_3 ; *
yin yang
---
C_1 C_3
---
yin = C_0
yang = g C_3 ; *
yin yang
---
C_0 C_3
если вы внимательно наблюдаете, это будет очевидно тебе то
- существует множество вселенных (на самом деле бесконечных), но
C_0- это единственная вселенная, которая началась сf. Другие запускаетсяg. -
C_0 C_nвсегда делает новое продолжениеC_max. Это потому чтоC_0это первая вселенная, котораяg cc idи не была исполнена. -
C_0 C_nи надпись@.C_n C_mкоторый n не 0 будет отображаться*. - время от времени программа выводится на
C_0 C_n, и я докажу, чтоC_0 C_nотделяется все более и более другим выражением, которое приводит к@*@**@***...
немного математики
предположим 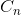
C_0 C_n называется.
Предположение: Когда C_0 C_n называется C_n текущий максимальный номер продолжение.
теперь 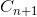
C_0 C_n такой:
yin = f C_n ; @
yang = g #C_{n+1}#
yin yang
Итак, мы заключаем, что:
Теорема I. Если C_0 C_n называется, он будет производить продолжение 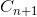
yin is C_n.
тогда следующий шаг -C_n C_{n+1}.
yin = C_{n-1}
yang = g C_{n+1} ; *
yin yang
почему yin is C_{n-1}, что когда C_n будучи создан он повиновался Теорема Я!--216-->.
а то C_{n-1} C_{n+1} называется, и мы знаем, что когда C_{n-1} создан, он также повиновался Теорема I. Итак, мы имеем C_{n-2} C_{n+1}.
C_{n+1}-это вариации. Итак, у нас есть вторая теорема:
Теорема II. Если C_n C_m, который n < m и n > 0 называется, станет C_{n-1} C_m.
и мы вручную проверили C_0 C_1 C_2 C_3. Они подчиняются предположение и все теоремы. И мы знаем, как сначала @ и это.
так мы можем написать картины ниже.
C_0 C_1 ; @ *
C_[1-0] C_2 ; @ * *
C_[2-0] C_3 ; @ * * *
...
это не так строго, но хотелось бы написать:
В. Е. Д.
как сказал другой ответ, мы сначала упростим (call-with-current-continuation (lambda (c) c)) С get-cc.
(let* ((yin
((lambda (cc) (display #\@) cc) get-cc))
(yang
((lambda (cc) (display #\*) cc) get-cc)) )
(yin yang))
теперь две лямбды - это просто идентичная функция, связанная с побочными эффектами. Назовем эти функции f (для display #\@) и g (для display #\*).
(let* ((yin (f get-cc))
(yang (g get-cc)))
(yin yang))
Далее нам нужно разработать порядок оценки. Чтобы быть ясным, я введу "выражение шага", которое делает каждый шаг оценки явным. Сначала давайте спросим: Что такое вышеуказанная функция требует?
это требует определения f и g. В выражении шага мы пишем
s0 f g =>
первый шаг-вычислить yin, но что требуют оценки (f get-cc), а после get-cc.
грубо говоря, get-cc дает вам значение, представляющее "текущее продолжение". Допустим, это s1 так как это следующий шаг. Так пишем
s0 f g => s1 f g ?
s1 f g cc =>
обратите внимание, что параметры scopeless, что означает f и g на s0 и s1 не обязательно то же самое, и они должны использоваться только в рамках текущего шага. Это делает контекстную информацию явной. Теперь, что значение cc? Поскольку это "текущее продолжение", это своего рода то же самое s1 С f и g привязано к тому же значению.
s0 f g => s1 f g (s1 f g)
s1 f g cc =>
как только у нас есть cc, мы можем оценить f get-cc. Кроме того, так как f не используется в следующих код, мы не должны передавать это значение.
s0 f g => s1 f g (s1 f g)
s1 f g cc => s2 g (f cc)
s2 g yin =>
следующий похож на yang. Но теперь у нас есть еще одно значение для передачи:yin.
s0 f g => s1 f g (s1 f g)
s1 f g cc => s2 g (f cc)
s2 g yin => s3 g yin (s3 g yin)
s3 g yin cc => s4 yin (g cc)
s4 yin yang =>
наконец, последний шаг-применить yang to yin.
s0 f g => s1 f g (s1 f g)
s1 f g cc => s2 g (f cc)
s2 g yin => s3 g yin (s3 g yin)
s3 g yin cc => s4 yin (g cc)
s4 yin yang => yin yang
это завершило построение выражения шага. Перевести его обратно на схему просто:
(let* ([s4 (lambda (yin yang) (yin yang))]
[s3 (lambda (yin cc) (s4 yin (g cc))]
[s2 (lambda (yin) (s3 yin ((lambda (cc) (s3 yin cc))))]
[s1 (lambda (cc) (s2 (f cc)))])
(s1 s1))
подробный порядок оценки (здесь лямбда внутри тела s2 было просто выражено как частичная оценка s3 yin, а не (lambda (cc) (s3 yin cc))):
(s1 s1)
=> (s2 (f s1))
=> @|(s2 s1)
=> @|(s3 s1 (s3 s1))
=> @|(s4 s1 (g (s3 s1)))
=> @*|(s4 s1 (s3 s1))
=> @*|(s1 (s3 s1))
=> @*|(s2 (f (s3 s1)))
=> @*@|(s2 (s3 s1))
=> @*@|(s2 (s3 s1))
=> @*@|(s3 (s3 s1) (s3 (s3 s1)))
=> @*@|(s4 (s3 s1) (g (s3 (s3 s1))))
=> @*@*|(s4 (s3 s1) (s3 (s3 s1)))
=> @*@*|(s3 s1 (s3 (s3 s1)))
=> @*@*|(s4 s1 (g (s3 (s3 s1))))
=> @*@**|(s4 s1 (s3 (s3 s1)))
=> @*@**|(s1 (s3 (s3 s1)))
=> ...
(помните, при оценке s2 или s4 параметр будет оцениваться первая
Это старая головоломка от мастера обфускации Дэвида Мадоре, который создан Unlambda. Головоломка была обсуждена comp.ленг.схема несколько раз.
хорошее решение от Тейлора Кэмпбелла: https://groups.google.com/d/msg/comp.lang.scheme/pUedvrKYY5w/uIjTc_T1LOEJ
оригинальный пост от David Madore (1999): https://groups.google.com/d/msg/comp.lang.scheme/Fysq_Wplxsw/awxEZ_uxW20J
