Как работает оператор двоеточия MATLAB?
как отметил в этот ответ Сэма Робертса и этот другой ответ gnovice, оператор двоеточия MATLAB (start:step:stop) создает вектор значений по-другому, что linspace делает. В частности, Сэм Робертс заявляет:
оператор двоеточия добавляет инкременты в начальную точку и вычитает декременты из конечной точки, чтобы достичь средней точки. Таким образом, он гарантирует, что выходной вектор так же симметричен, как вероятный.
однако официальная документация об этом из MathWorks была удалена с их сайта.
если описание Сэма правильное, разве ошибки в размерах шага не будут симметричными?
>> step = 1/3;
>> C = 0:step:5;
>> diff(C) - step
ans =
1.0e-15 *
Columns 1 through 10
0 0 0.0555 -0.0555 -0.0555 0.1665 -0.2776 0.6106 -0.2776 0.1665
Columns 11 through 15
0.1665 -0.2776 -0.2776 0.6106 -0.2776
интересные вещи, чтобы отметить об операторе двоеточия:
-
его значения зависят от ее длины:
>> step = 1/3; >> C = 0:step:5; >> X = 0:step:3; >> C(1:10) - X ans = 1.0e-15 * 0 0 0 0 0 -0.2220 0 -0.4441 0.4441 0 -
он может генерировать повторяющиеся значения, если они округлено:
>> E = 1-eps : eps/4 : 1+eps; >> E-1 ans = 1.0e-15 * -0.2220 -0.2220 -0.1110 0 0 0 0 0.2220 0.2220 -
существует допуск для последнего значения, если размер шага создает значение чуть выше конца, это конечное значение все еще используется:
>> A = 0 : step : 5-2*eps(5) A = Columns 1 through 10 0 0.3333 0.6667 1.0000 1.3333 1.6667 2.0000 2.3333 2.6667 3.0000 Columns 11 through 16 3.3333 3.6667 4.0000 4.3333 4.6667 5.0000 >> A(end) == 5 - 2*eps(5) ans = logical 1 >> step*15 - 5 ans = 0
1 ответов
удаленная страница, на которую ссылается Сэм по-прежнему архивируется на обратном пути машины. К счастью, даже прилагаемый M-файл colonop это тоже есть. И кажется, что эта функция все еще соответствует тому, что делает MATLAB (я на R2017a):
>> all(0:step:5 == colonop(0,step,5))
ans =
logical
1
>> all(-pi:pi/21:pi == colonop(-pi,pi/21,pi))
ans =
logical
1
я повторю здесь, что функция делает для общего случая (есть некоторые ярлыки для генерации целочисленных векторов и обработки особых случаев). Я заменяю имена переменных функции с более значимыми. Входы start, step и stop.
сначала он вычисляет сколько шагов между start и stop. Если последний шаг превышает stop более чем допуском, не принимается:
n = round((stop-start)/step);
tol = 2.0*eps*max(abs(start),abs(stop));
sig = sign(step);
if sig*(start+n*step - stop) > tol
n = n - 1;
end
это объясняет последнее замечание, упомянутое в вопросе.
затем он вычисляет значение последнего элемента и удостоверяется, что он не превышает stop значение, даже если его отпустили мимо него в предыдущем расчете.
last = start + n*step;
if sig*(last-stop) > -tol
last = stop;
end
вот почему значение lasat в векторе A в вопросе на самом деле есть stop значение, последнее значение.
затем он вычисляет выходной массив в двух частях, как объявлено: левая и правая половины массива заполняются независимо:
out = zeros(1,n+1);
k = 0:floor(n/2);
out(1+k) = start + k*step;
out(n+1-k) = last - k*step;
обратите внимание, что они не заполняются приращением, а вычислением целого массива и умножением его на размер шага, как и linspace делает. Этот exaplains замечание о массиве E в этом вопросе. Разница в том, что правая половина массива заполняется путем вычитания этих значений из last значение.
в качестве последнего шага для нечетных массивов среднее значение вычисляется отдельно, чтобы убедиться, что оно лежит ровно на половине двух конечных точек:
if mod(n,2) == 0
out(n/2+1) = (start+last)/2;
end
полная функция colonop копируется внизу.
обратите внимание, что заполнение левого и правая сторона массива отдельно не означает, что ошибки в размерах шагов должны быть идеально симметричными. Эти ошибки задаются ошибками roundoff. Но это имеет значение, где stop точка не достигается точно размером шага, как в случае array A в этом вопросе. В этом случае немного более короткий размер шага берется в середине массива, а не в конце:
>> step=1/3;
>> A = 0 : step : 5-2*eps(5);
>> A/step-(0:15)
ans =
1.0e-14 *
Columns 1 through 10
0 0 0 0 0 0 0 -0.0888 -0.4441 -0.5329
Columns 11 through 16
-0.3553 -0.3553 -0.5329 -0.5329 -0.3553 -0.5329
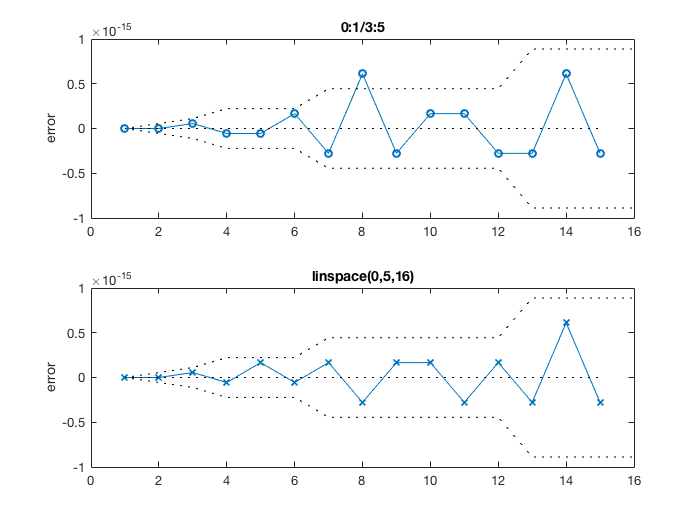
но даже в том случае, когда stop точка достигнута точно, какая-то дополнительная ошибка накапливается посередине. Возьмем для примера массив C в этом вопросе. Это накопление ошибок не происходит с linspace:
C = 0:1/3:5;
lims = eps(C);
subplot(2,1,1)
plot(diff(C)-1/3,'o-')
hold on
plot(lims,'k:')
plot(-lims,'k:')
plot([1,15],[0,0],'k:')
ylabel('error')
title('0:1/3:5')
L = linspace(0,5,16);
subplot(2,1,2)
plot(diff(L)-1/3,'x-')
hold on
plot(lims,'k:')
plot(-lims,'k:')
plot([1,15],[0,0],'k:')
title('linspace(0,5,16)')
ylabel('error')
colonop:
function out = colonop(start,step,stop)
% COLONOP Demonstrate how the built-in a:d:b is constructed.
%
% v = colonop(a,b) constructs v = a:1:b.
% v = colonop(a,d,b) constructs v = a:d:b.
%
% v = a:d:b is not constructed using repeated addition. If the
% textual representation of d in the source code cannot be
% exactly represented in binary floating point, then repeated
% addition will appear to have accumlated roundoff error. In
% some cases, d may be so small that the floating point number
% nearest a+d is actually a. Here are two imporant examples.
%
% v = 1-eps : eps/4 : 1+eps is the nine floating point numbers
% closest to v = 1 + (-4:1:4)*eps/4. Since the spacing of the
% floating point numbers between 1-eps and 1 is eps/2 and the
% spacing between 1 and 1+eps is eps,
% v = [1-eps 1-eps 1-eps/2 1 1 1 1 1+eps 1+eps].
%
% Even though 0.01 is not exactly represented in binary,
% v = -1 : 0.01 : 1 consists of 201 floating points numbers
% centered symmetrically about zero.
%
% Ideally, in exact arithmetic, for b > a and d > 0,
% v = a:d:b should be the vector of length n+1 generated by
% v = a + (0:n)*d where n = floor((b-a)/d).
% In floating point arithmetic, the delicate computatations
% are the value of n, the value of the right hand end point,
% c = a+n*d, and symmetry about the mid-point.
if nargin < 3
stop = step;
step = 1;
end
tol = 2.0*eps*max(abs(start),abs(stop));
sig = sign(step);
% Exceptional cases.
if ~isfinite(start) || ~isfinite(step) || ~isfinite(stop)
out = NaN;
return
elseif step == 0 || start < stop && step < 0 || stop < start && step > 0
% Result is empty.
out = zeros(1,0);
return
end
% n = number of intervals = length(v) - 1.
if start == floor(start) && step == 1
% Consecutive integers.
n = floor(stop) - start;
elseif start == floor(start) && step == floor(step)
% Integers with spacing > 1.
q = floor(start/step);
r = start - q*step;
n = floor((stop-r)/step) - q;
else
% General case.
n = round((stop-start)/step);
if sig*(start+n*step - stop) > tol
n = n - 1;
end
end
% last = right hand end point.
last = start + n*step;
if sig*(last-stop) > -tol
last = stop;
end
% out should be symmetric about the mid-point.
out = zeros(1,n+1);
k = 0:floor(n/2);
out(1+k) = start + k*step;
out(n+1-k) = last - k*step;
if mod(n,2) == 0
out(n/2+1) = (start+last)/2;
end