Как реализовать функцию Softmax в Python
С класс глубокого обучения Udacity, softmax y_i - это просто экспонента, деленная на сумму экспоненты всего вектора Y:
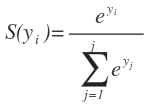
здесь S(y_i) является функцией softmax y_i и e является экспоненциальным и j нет. столбцов во входном векторе Ю.
Я пробовал следующие:
import numpy as np
def softmax(x):
"""Compute softmax values for each sets of scores in x."""
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum()
scores = [3.0, 1.0, 0.2]
print(softmax(scores))
возвращает:
[ 0.8360188 0.11314284 0.05083836]
но предлагаемое решение было:
def softmax(x):
"""Compute softmax values for each sets of scores in x."""
return np.exp(x) / np.sum(np.exp(x), axis=0)
которая производит тот же результат, что и первая реализация, хотя первая реализация явно принимает разность каждого столбца и max, а затем делится на сумму.
может кто-нибудь показать математически, почему? Один правильный, а другой неправильный?
аналогична ли реализация с точки зрения сложности кода и времени? Что больше эффективно?
16 ответов
Они оба верны, но ваш предпочтительнее с точки зрения числовой стабильности.
вы начинаете с
e ^ (x - max(x)) / sum(e^(x - max(x))
, воспользовавшись тем, что^(б - с) = (А^Б)/(а^в)
= e ^ x / (e ^ max(x) * sum(e ^ x / e ^ max(x)))
= e ^ x / sum(e ^ x)
что и говорит другой ответ. Вы можете заменить max (x) любой переменной, и она будет отменена.
(Ну... здесь много путаницы, как в вопросе, так и в ответах...)
для начала, два решения (т. е. ваше и предлагаемое) являются не эквивалентны; они быть эквивалентным только для частного случая массивов 1-D баллов. Вы бы обнаружили это, если бы вы попробовали также массив 2-D баллов в Примере Udacity quiz.
Results-wise, единственная фактическая разница между двумя решениями the :
import numpy as np
# your solution:
def your_softmax(x):
"""Compute softmax values for each sets of scores in x."""
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum()
# correct solution:
def softmax(x):
"""Compute softmax values for each sets of scores in x."""
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum(axis=0) # only difference
как я уже сказал, для массива 1-D баллов результаты действительно идентичны:
scores = [3.0, 1.0, 0.2]
print(your_softmax(scores))
# [ 0.8360188 0.11314284 0.05083836]
print(softmax(scores))
# [ 0.8360188 0.11314284 0.05083836]
your_softmax(scores) == softmax(scores)
# array([ True, True, True], dtype=bool)
тем не менее, вот результаты для массива 2-D баллов, приведенных в викторине Udacity в качестве тестового примера:
scores2D = np.array([[1, 2, 3, 6],
[2, 4, 5, 6],
[3, 8, 7, 6]])
print(your_softmax(scores2D))
# [[ 4.89907947e-04 1.33170787e-03 3.61995731e-03 7.27087861e-02]
# [ 1.33170787e-03 9.84006416e-03 2.67480676e-02 7.27087861e-02]
# [ 3.61995731e-03 5.37249300e-01 1.97642972e-01 7.27087861e-02]]
print(softmax(scores2D))
# [[ 0.09003057 0.00242826 0.01587624 0.33333333]
# [ 0.24472847 0.01794253 0.11731043 0.33333333]
# [ 0.66524096 0.97962921 0.86681333 0.33333333]]
результаты различны-второе одно действительно идентично с одним предпологаемым в Udacity quiz, где все столбцы действительно суммируются до 1, что не относится к первому (неправильному) результату.
Итак, вся суета была на самом деле для детали реализации -
Я бы сказал, что, хотя оба правильны математически, реализация мудра, первый лучше. При вычислении softmax, промежуточные значения могут стать очень большими. Деления двух больших чисел может быть численно неустойчивым. эти заметки (из Стэнфорда) упомяните трюк нормализации, который по существу является тем, что вы делаете.
Итак, это действительно комментарий к ответу desertnaut's, но я пока не могу прокомментировать его из-за моей репутации. Как он указал, ваша версия верна, только если ваш вход состоит из одного образца. Если ваш ввод состоит из нескольких образцов, это неправильно. однако решение дезертнота также неверно. проблема в том, что как только он принимает 1-мерный вход, а затем он принимает 2-мерный вход. Позвольте мне показать вам это.
import numpy as np
# your solution:
def your_softmax(x):
"""Compute softmax values for each sets of scores in x."""
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum()
# desertnaut solution (copied from his answer):
def desertnaut_softmax(x):
"""Compute softmax values for each sets of scores in x."""
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum(axis=0) # only difference
# my (correct) solution:
def softmax(z):
assert len(z.shape) == 2
s = np.max(z, axis=1)
s = s[:, np.newaxis] # necessary step to do broadcasting
e_x = np.exp(z - s)
div = np.sum(e_x, axis=1)
div = div[:, np.newaxis] # dito
return e_x / div
давайте возьмем desertnauts пример:
x1 = np.array([[1, 2, 3, 6]]) # notice that we put the data into 2 dimensions(!)
это выход:
your_softmax(x1)
array([[ 0.00626879, 0.01704033, 0.04632042, 0.93037047]])
desertnaut_softmax(x1)
array([[ 1., 1., 1., 1.]])
softmax(x1)
array([[ 0.00626879, 0.01704033, 0.04632042, 0.93037047]])
вы можете видеть, что версия desernauts потерпит неудачу в этой ситуации. (Это не было бы, если бы вход был только одномерным, как np.массив([1, 2, 3, 6]).
теперь давайте использовать 3 образца, так как именно по этой причине мы используем 2-мерный вход. Следующий x2 не совпадает с примером из desernauts.
x2 = np.array([[1, 2, 3, 6], # sample 1
[2, 4, 5, 6], # sample 2
[1, 2, 3, 6]]) # sample 1 again(!)
этот входной сигнал состоит из серии с 3 образцами. Но образец один и три по сути одинаковы. Теперь мы ожидаем 3 строки активации softmax, где первая должна быть такой же, как и третья, а также такая же, как наша активация x1!
your_softmax(x2)
array([[ 0.00183535, 0.00498899, 0.01356148, 0.27238963],
[ 0.00498899, 0.03686393, 0.10020655, 0.27238963],
[ 0.00183535, 0.00498899, 0.01356148, 0.27238963]])
desertnaut_softmax(x2)
array([[ 0.21194156, 0.10650698, 0.10650698, 0.33333333],
[ 0.57611688, 0.78698604, 0.78698604, 0.33333333],
[ 0.21194156, 0.10650698, 0.10650698, 0.33333333]])
softmax(x2)
array([[ 0.00626879, 0.01704033, 0.04632042, 0.93037047],
[ 0.01203764, 0.08894682, 0.24178252, 0.65723302],
[ 0.00626879, 0.01704033, 0.04632042, 0.93037047]])
Я надеюсь, вы видите, что это только в случае с моим решением.
softmax(x1) == softmax(x2)[0]
array([[ True, True, True, True]], dtype=bool)
softmax(x1) == softmax(x2)[2]
array([[ True, True, True, True]], dtype=bool)
кроме того, вот результаты реализации tensorflows softmax:
import tensorflow as tf
import numpy as np
batch = np.asarray([[1,2,3,6],[2,4,5,6],[1,2,3,6]])
x = tf.placeholder(tf.float32, shape=[None, 4])
y = tf.nn.softmax(x)
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(y, feed_dict={x: batch})
и в итоге:
array([[ 0.00626879, 0.01704033, 0.04632042, 0.93037045],
[ 0.01203764, 0.08894681, 0.24178252, 0.657233 ],
[ 0.00626879, 0.01704033, 0.04632042, 0.93037045]], dtype=float32)
sklearn также предлагает реализацию softmax
from sklearn.utils.extmath import softmax
import numpy as np
x = np.array([[ 0.50839931, 0.49767588, 0.51260159]])
softmax(x)
# output
array([[ 0.3340521 , 0.33048906, 0.33545884]])
С математической точки зрения обе стороны равны.
и вы можете легко доказать это. Давайте!--0-->. Теперь ваша функция softmax возвращает вектор, i-я координата которого равна
обратите внимание, что это работает для любого m, потому что для всех (даже сложных) чисел e^m != 0
С точки зрения вычислительной сложности, они также эквивалентны и оба работают в
O(n)время, гдеn- размер вектора.С устойчивость точка зрения, первое решение предпочтительнее, потому что
e^xрастет очень быстро, и даже для довольно малых значенийxон будет переполнен. Вычитание максимального значения позволяет избавиться от этого переполнения. Чтобы практически испытать материал, о котором я говорил, попробуйте накормитьx = np.array([1000, 5])в ваши функции. Один вернет правильную вероятность, второй переполнения сnanне связано с вопросом, но ваше решение работает только для векторов (Udacity quiz хочет, чтобы вы вычисляли его и для матриц). Чтобы исправить это, вам нужно использовать
sum(axis=0)
здесь вы можете узнать, почему они использовали - max.
оттуда:
"когда вы пишете код для вычисления функции Softmax на практике, промежуточные сроки могут быть очень большими из-за экспоненты. Деления больших чисел может быть численно неустойчивым, поэтому важно использовать трюк нормализации."
Я написал функцию, применяющую softmax по любой оси:
def softmax(X, theta = 1.0, axis = None):
"""
Compute the softmax of each element along an axis of X.
Parameters
----------
X: ND-Array. Probably should be floats.
theta (optional): float parameter, used as a multiplier
prior to exponentiation. Default = 1.0
axis (optional): axis to compute values along. Default is the
first non-singleton axis.
Returns an array the same size as X. The result will sum to 1
along the specified axis.
"""
# make X at least 2d
y = np.atleast_2d(X)
# find axis
if axis is None:
axis = next(j[0] for j in enumerate(y.shape) if j[1] > 1)
# multiply y against the theta parameter,
y = y * float(theta)
# subtract the max for numerical stability
y = y - np.expand_dims(np.max(y, axis = axis), axis)
# exponentiate y
y = np.exp(y)
# take the sum along the specified axis
ax_sum = np.expand_dims(np.sum(y, axis = axis), axis)
# finally: divide elementwise
p = y / ax_sum
# flatten if X was 1D
if len(X.shape) == 1: p = p.flatten()
return p
вычитание max, как описывали другие пользователи, является хорошей практикой. Я написал подробный пост об этом здесь.
чтобы предложить альтернативное решение, рассмотрим случаи, когда ваши аргументы чрезвычайно велики по величине, так что exp(x) будет underflow (в отрицательном случае) или переполнение (в положительном случае). Здесь вы хотите оставаться в пространстве журнала как можно дольше, экспонентируя только в конце, где вы можете доверять результату, будет хорошо себя вести.
import scipy.special as sc
import numpy as np
def softmax(x: np.ndarray) -> np.ndarray:
return np.exp(x - sc.logsumexp(x))
Я бы предложил так-
def softmax(z):
z_norm=np.exp(z-np.max(z,axis=0,keepdims=True))
return(np.divide(z_norm,np.sum(z_norm,axis=0,keepdims=True)))
он будет работать как для стохастика, так и для партии. Более подробно см. https://medium.com/@ravish1729/analysis-of-softmax-function-ad058d6a564d
для поддержания числовой стабильности следует вычесть max(x). Ниже приведен код для функции softmax;
def softmax (x):
if len(x.shape) > 1:
tmp = np.max(x, axis = 1)
x -= tmp.reshape((x.shape[0], 1))
x = np.exp(x)
tmp = np.sum(x, axis = 1)
x /= tmp.reshape((x.shape[0], 1))
else:
tmp = np.max(x)
x -= tmp
x = np.exp(x)
tmp = np.sum(x)
x /= tmp
return x
Я хотел бы дополнить немного больше понимания проблемы. Здесь правильно вычитать max массива. Но если вы запустите код в другом сообщении, вы обнаружите, что он не дает вам правильного ответа, когда массив имеет 2D или более высокие размеры.
здесь я даю вам несколько советов:
- чтобы получить max, попробуйте сделать это вдоль оси x, вы получите массив 1D.
- измените свой максимальный массив на оригинальную форму.
- Do np.опыт получить экспоненциальное значение.
- Do np.сумма по оси.
- получить окончательные результаты.
следуйте за результатом, вы получите правильный ответ, выполнив векторизацию. Поскольку это связано с домашним заданием колледжа, я не могу опубликовать точный код здесь, но я хотел бы дать больше предложений, если вы не понимаете.
уже ответил подробно в приведенных выше ответах. max вычитается, чтобы избежать переполнения. Я добавляю здесь еще одну реализацию в python3.
import numpy as np
def softmax(x):
mx = np.amax(x,axis=1,keepdims = True)
x_exp = np.exp(x - mx)
x_sum = np.sum(x_exp, axis = 1, keepdims = True)
res = x_exp / x_sum
return res
x = np.array([[3,2,4],[4,5,6]])
print(softmax(x))
целью функции softmax является сохранение соотношения векторов в отличие от раздавливания конечных точек сигмоидом по мере насыщения значений (то есть, как правило, + / -1 (tanh) или от 0 до 1 (logistical)). Это связано с тем, что он сохраняет больше информации о скорости изменения в конечных точках и, следовательно, более применим к нейронным сетям с кодировкой 1-of-N (т. е. если мы раздавили конечные точки, было бы сложнее дифференцировать 1-of-N выходной класс, потому что мы не можем сказать какой из них" самый большой "или" самый маленький", потому что их раздавили.); кроме того, он делает общую выходную сумму до 1, и явный победитель будет ближе к 1, в то время как другие числа, близкие друг к другу, будут суммироваться до 1/p, где p-количество выходных нейронов с аналогичными значениями.
цель вычитания максимального значения из вектора заключается в том, что при выполнении показателей e^y вы можете получить очень высокое значение, которое зажимает поплавок при максимальном значении, ведущем к галстуку, что не так в этом примере. Это становится большой проблемой, если вычесть максимальное значение, чтобы сделать отрицательное число, то у вас есть отрицательный показатель, который быстро сжимает значения, изменяющие отношение, что и произошло в вопросе плаката и дало неправильный ответ.
ответ, предоставленный Udacity, ужасно неэффективен. Первое, что нам нужно сделать, это вычислить e^y_j для всех векторных компонентов, сохранить эти значения, затем суммировать их и разделить. Где Udacity испортили они вычислите e^y_j дважды!!! Вот правильный ответ:
def softmax(y):
e_to_the_y_j = np.exp(y)
return e_to_the_y_j / np.sum(e_to_the_y_j, axis=0)
цель состояла в том, чтобы достичь аналогичных результатов с помощью Numpy и Tensorflow. Единственное изменение от исходного ответа - на np.sum API-интерфейс.
первоначальный подход : axis=0 - это, однако, не дает предполагаемых результатов, когда размеры N.
изменен подход: axis=len(e_x.shape)-1 - всегда суммировать в последнем измерении. Это дает аналогичные результаты, как функция softmax tensorflow.
def softmax_fn(input_array):
"""
| **@author**: Prathyush SP
|
| Calculate Softmax for a given array
:param input_array: Input Array
:return: Softmax Score
"""
e_x = np.exp(input_array - np.max(input_array))
return e_x / e_x.sum(axis=len(e_x.shape)-1)