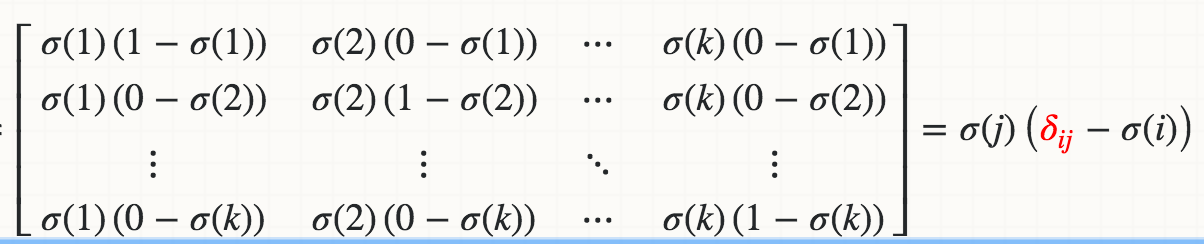Как реализовать производную Softmax независимо от любой функции потерь?

для библиотеки нейронных сетей я реализовал некоторые функции активации и функции потерь и их производные. Их можно комбинировать произвольно, и производная на выходных слоях просто становится произведением производной потерь и производной активации.

однако мне не удалось реализовать производную функции активации Softmax независимо от любой функции потерь. Из-за нормализации, т. е. знаменателя в уравнении, изменение одного входа активация изменяет все выходные активации, а не только одну.

вот моя реализация Softmax, где производная не проверяет градиент примерно на 1%. Как я могу реализовать производную Softmax, чтобы ее можно было объединить с любой функцией потерь?

import numpy as np


class Softmax:

    def compute(self, incoming):
        exps = np.exp(incoming)
        return exps / exps.sum()

    def delta(self, incoming, outgoing):
        exps = np.exp(incoming)
        others = exps.sum() - exps
        return 1 / (2 + exps / others + others / exps)


activation = Softmax()
cost = SquaredError()

outgoing = activation.compute(incoming)
delta_output_layer = activation.delta(incoming) * cost.delta(outgoing)
9
backpropagation derivative neural-network regression softmax

2 ответов

математически производная Softmax (Xi) относительно Xj равна:

enter image description here

где красная Дельта-Дельта Кронекера.

Если вы последовательно реализовать:

def softmax_grad(s):
    # input s is softmax value of the original input x. Its shape is (1,n) 
    # e.i. s = np.array([0.3,0.7]), x = np.array([0,1])

    # make the matrix whose size is n^2.
    jacobian_m = np.diag(s)

    for i in range(len(jacobian_m)):
        for j in range(len(jacobian_m)):
            if i == j:
                jacobian_m[i][j] = s[i] * (1-s[i])
            else: 
                jacobian_m[i][j] = -s[i]*s[j]
    return jacobian_m

тест:

In [95]: x
Out[95]: array([1, 2])

In [96]: softmax(x)
Out[96]: array([ 0.26894142,  0.73105858])

In [97]: softmax_grad(softmax(x))
Out[97]: 
array([[ 0.19661193, -0.19661193],
       [-0.19661193,  0.19661193]])

Если вы реализуете в векторизованной версии:

soft_max = softmax(x)    

# reshape softmax to 2d so np.dot gives matrix multiplication

def softmax_grad(softmax):
    s = softmax.reshape(-1,1)
    return np.diagflat(s) - np.dot(s, s.T)

softmax_grad(soft_max)

#array([[ 0.19661193, -0.19661193],
#       [-0.19661193,  0.19661193]])
4

это должно быть так: (x-вход в слой softmax, а DY-Дельта, исходящая из потери над ним)

    dx = y * dy
    s = dx.sum(axis=dx.ndim - 1, keepdims=True)
    dx -= y * s

    return dx

но способ вычисления ошибки должен быть:

    yact = activation.compute(x)
    ycost = cost.compute(yact)
    dsoftmax = activation.delta(x, cost.delta(yact, ycost, ytrue))

объяснение: потому что delta функция является частью алгоритма backpropagation, его обязанностью является умножение вектора dy (в моем коде outgoing в вашем случае) на Якобиан

10