Как умножить каждый столбец матрицы A на каждую строку матрицы B и суммировать результирующие матрицы в Matlab?

У меня есть проблема, которую, я надеюсь, можно легко решить. А-Н матрица G, B - NG матрица. Цель состоит в том, чтобы получить матрицу c

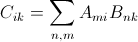
enter image description here

что равно умножению каждого столбца транспонированного A на каждую строку B и суммированию результирующих матриц; общее число таких матриц перед суммированием равно NN, их размер GG Это можно легко сделать в MatLab с двумя на-петли:

N=5;
G=10;
A=rand(N,G);
B=rand(N,G);
C=zeros(G);
for n=1:1:N
    for m=1:1:N
        C=C+A(m,:)'*B(n,:);
    end
end

однако, для больших матрицы довольно медленные.

Итак, мой вопрос: есть ли более эффективный способ вычисления матрицы C в Matlab?

спасибо

6
matlab matrix matrix-multiplication performance

3 ответов

если вы запишете все это для двух матриц 3×3, вы обнаружите, что операция в основном равна этому:

C = bsxfun(@times, sum(B), sum(A).');

запуск каждого из ответов здесь N=50, G=100 и повторяя каждый метод в 100 раз:

Elapsed time is 13.839893 seconds. %// OP's original method
Elapsed time is 19.773445 seconds. %// Luis' method
Elapsed time is 0.306447 seconds.  %// Robert's method
Elapsed time is 0.005036 seconds.  %// Rody's method

(коэффициент ≈ 4000 между самым быстрым и самым медленным методом...)

7

Я думаю, что это должно значительно улучшить производительность

C = zeros(G);
for n = 1:N
   C = C + sum(A,1)'*B(n,:);
end

вы избегаете одного цикла, а также должны избегать проблем с нехваткой памяти. По моим бенчмаркинг, это примерно в 20 раз быстрее, чем подход с двумя петлями. (Обратите внимание, мне пришлось тестировать в Octace, так как у меня нет MATLAB на этом ПК).

3

использовать bsxfun вместо петель, а потом sum дважды: 

C = sum(sum(bsxfun(@times, permute(A, [2 3 1]), permute(B,[3 2 4 1])), 3), 4);
2