Как вычислить евклидово расстояние между двумя точками, определенными матрицей, содержащей x, y?
Я очень потерялся в расчет евклидова расстояния. Я нашел функции dist2{SpatialTools} или rdist{fields} для этого, но они работают не так, как ожидалось.
Я полагаю, что одна точка имеет две координаты в картезианской системе,поэтому [x, y]. Чтобы измерить расстояние между 2 точками (определенными строкой), мне нужно 4 координаты для 2 точек, поэтому ПУНКТ А: [x1,y1]] точка B: [x2, y2]
очки координация:
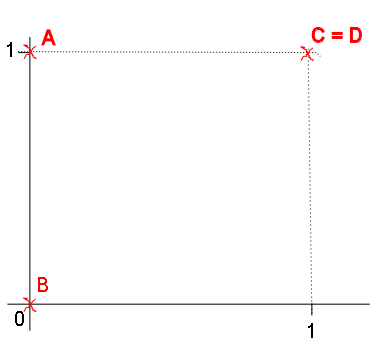
A[0,1]
B[0,0]
C[1,1]
D[1,1]
у меня есть две матрицы: x1(существуют A и C, определенные строками) и x2 (содержит B и D). Написано в матрице:
library("SpatialTools")
x1<-matrix(c(0,1,1,1), nrow = 2, ncol=2, byrow=TRUE)
x2<-matrix(c(0,0,1,1), nrow = 2, ncol=2, byrow=TRUE)
так я получаю
> x1
[,1] [,2]
[1,] 0 1 #(as xy coordinates of A point)
[2,] 1 1 #(same for C point)
> x2
[,1] [,2]
[1,] 0 0 #(same for B point)
[2,] 1 1 #(same for D point)
для вычисления евклидова расстояния между
A <-> B # same as x1[1,] <-> x2[1,]
C <-> D # same as x1[2,] <-> x2[2,]
Я предполагаю получить EuclidDist:
> x1 x2 EuclidDist
[,1] [,2] [,1] [,2]
[1,] 0 1 #A [1,] 0 0 #B 1
[2,] 1 1 #B [2,] 1 1 #D 0
Я хотел бы просто получить вектор расстояний между двумя точками идентифицировано координатами [x,y], однако, используя dist2 Я получаю матрицу:
> dist2(x1,x2)
[,1] [,2]
[1,] 1.000000 1
[2,] 1.414214 0
мой вопрос в том, какие числа описывают реальное Евклидово расстояние между A-B и C-D от этой матрицы? Я что-то не так понял? Большое спасибо за каждый совет или любое объяснение.
4 ответов
Если вы просто хотите вектор, что-то вроде этого будет работать для вас.
попробуйте что-то вроде этого:
euc.dist <- function(x1, x2) sqrt(sum((x1 - x2) ^ 2))
library(foreach)
foreach(i = 1:nrow(x1), .combine = c ) %do% euc.dist(x1[i,],x2[i,])
это будет работать для любых размеров.
Если вы не хотите использовать foreach, вы можете использовать простой цикл:
dist <- NULL
for(i in 1:nrow(x1)) dist[i] <- euc.dist(x1[i,],x2[i,])
dist
хотя, я бы рекомендовал foreach (потому что это очень легко для различных задач, как это). Подробнее об этом читайте в документации к пакету.
диагональ-это то, что вы ищете. Выходная матрица dist2 показывает расстояние между всеми точками. Номер строки на выходе соответствует строке на первом входе, а столбец на выходе соответствует строке на втором входе. Вот диаграмма, надеюсь, что это имеет смысл (это то, что я хочу, чтобы Stack Overflow поддерживал MathJax):
dist2( A_x A_y C_x C_y ( AC AD
B_x B_y , D_x D_y ) = BC BD )
dist2( x1 , x2 ) = result
в вашем случае, вы хотите, чтобы расстояние от первой точки x1 к первому пункту x2, затем второй пункт x1 второй пункт x2, следовательно, диагональ.
если у вас много данных, и вы заботитесь только о соответствующих парах, вам будет намного лучше вычислить это напрямую:
> x1 <- matrix(c(0, 1, 1, 1), ncol = 2, byrow = T)
> x2 <- matrix(c(0, 0, 1, 1), ncol = 2, byrow = T)
> sqrt(rowSums((x1 - x2)^2))
[1] 1 0
если у вас много данных (миллионы точек), это может быть стоит использовать foreach как предлагает @Shambho.
library(rgdal)
library(sp)
##**COORDINATES** DATAFRAME THAT CONTENT THE LATITUDE (LAT) AND LONGITUDE
##(LON) IN THE COORDINATE REFERENT SYSTEM (CRS) WGS84.
coordinates(COORDINATES) <- ~ LON + LAT
proj4string(COORDINATES) <- CRS("+proj=longlat +datum=WGS84") #ASSIGN THE CRS
Zone <- input$Zone #UTM ZONE FOR YOUR COUNTRY
COORDINATES <- spTransform(COORDINATES, CRS(paste("+proj=utm", " +zone=",
Zone, " +ellps=WGS84", " +datum=WGS84", "
+units=m", sep=""))) #REPROJECT THE CRS
COORDINATES <- as.data.frame(COORDINATES)
X <- COORDINATES$LON #EXTRACT THE LOGITUDE VECTOR
Y <- COORDINATES$LAT #EXTRACT THE LATITUDE VECTOR
MX1 <- X %*% t(X) #CREATE A MATRIX FOR LONGITUDE VECTOR
MX2 <- matrix(rep(t(X),nrow(COORDINATES)), ncol = nrow(COORDINATES),
nrow = nrow(COORDINATES)) #CREATE A MATRIX FOR REPEAT LONGITUDE VECTOR
MX <- MX1/MX2 #DEFENITIVE MATRIX FOR LONGITUDE VECTORS
MX <- abs((MX-MX2)**2) #SQUARE SUM OF LONGITUDE VECTORS
colnames(MX)<- paste(COORDINATES$STATION) #ASSIGN COLNAMES
rownames(MX)<- paste(COORDINATES$STATION) #ASSIGN ROWNAMES
MY1 <- Y %*% t(Y) #CREATE A MATRIX FOR LATITUDE VECTOR
MY2 <- matrix(rep(t(Y), nrow(COORDINATES)), ncol = nrow(COORDINATES),
nrow = nrow(COORDINATES)) #CREATE A MATRIX FOR REPEAT LATITUDE VECTOR
MY <- MY1/MY2 #DEFENITIVE MATRIX FOR LATITUDE VECTORS
MY <- abs((MY-MY2)*2) #SQUARE SUM OF LONGITUDE VECTORS
colnames(MY)<- paste(COORDINATES$STATION) #ASSIGN COLNAMES
rownames(MY)<- paste(COORDINATES$STATION) #ASSIGN ROWNAMES
EUCLIDEAND <- round((sqrt(MX+MY)/1000), digits = 0) #EUCLIDEAN DISTANCE FOR THESE COORDINATES
EUCLIDEAND <- as.data.frame(EUCLIDEAND)
вы всегда можете просто применить истинное уравнение (написанное для пакета sqldf, но его можно легко преобразовать):
sum(SQRT(power(a.LONG-b.lon,2)+power(a.LAT-b.lat,2))) AS DISTANCE
