Как вычислить PI в C#?
21 ответов
Если вы хотите рекурсии:
PI = 2 * (1 + 1/3 * (1 + 2/5 * (1 + 3/7 * (...))))
это станет, после некоторого переписывания:
PI = 2 * F(1);
С F (i):
double F (int i) {
return 1 + i / (2.0 * i + 1) * F(i + 1);
}
Исаак Ньютон (вы, возможно, слышали о нем раньше ;)) придумал этот трюк. Обратите внимание, что я опустил конечное условие, чтобы оно было простым. В реальной жизни он тебе нужен.
Как использовать:
double pi = Math.PI;
Если вы хотите лучшую точность, чем это, вам нужно будет использовать алгоритмическую систему и десятичный тип.
есть несколько очень, очень старое, Я удивлен, что не вижу здесь.
atan (1) = = PI/4, поэтому старый каштан, когда надежная функция дуги-тангенса присутствует 4 * atan (1).
очень симпатичная оценка с фиксированным коэффициентом, которая делает старый Western 22/7 похожим на грязь это 355/113, что хорошо для нескольких десятичных знаков (по крайней мере, три или четыре, я думаю). В некоторых случаях это даже достаточно хорошо для целочисленной арифметики: умножить на 355, а затем разделить на 113.
355/113 также легко зафиксировать в памяти (для некоторых людей, во всяком случае): сосчитайте один, один, три, три, пять, пять и помните, что вы называете цифры в знаменателе и числителе (если вы забудете, какой триплет идет сверху, мысль микросекунды обычно собирается выпрямить его).
обратите внимание, что 22/7 дает вам: 3.14285714, что неверно в тысячных.
355/113 дает вам 3.14159292, который не ошибается, пока десять-милионной.
Acc. to / usr / include / math.h на моем поле, M_PI #define'D как: 3.14159265358979323846 что, вероятно, хорошо, насколько это происходит.
урок, который вы получаете от оценки PI, заключается в том, что есть много способов сделать это, никто никогда не будет совершенным, и вы должны сортировать их по предназначению.
355/113-это старая китайская оценка, и я считаю, что она датируется 22/7 многими годами. Этому меня научил профессор физики, когда я был старшекурсник.
Если вы внимательно посмотрите на это действительно хорошее руководство:
вы найдете на странице 70 эту милую реализацию (с небольшими изменениями с моей стороны):
static decimal ParallelPartitionerPi(int steps)
{
decimal sum = 0.0;
decimal step = 1.0 / (decimal)steps;
object obj = new object();
Parallel.ForEach(
Partitioner.Create(0, steps),
() => 0.0,
(range, state, partial) =>
{
for (int i = range.Item1; i < range.Item2; i++)
{
decimal x = (i - 0.5) * step;
partial += 4.0 / (1.0 + x * x);
}
return partial;
},
partial => { lock (obj) sum += partial; });
return step * sum;
}
хороший обзор различных алгоритмов:
Я не уверен в сложности, заявленной для алгоритма Гаусса-Лежандра-Саламина в первой ссылке(я бы сказал O(N log^2(N) log(log (N)))).
Я призываю вас попробовать, хотя конвергенция действительно быстро.
кроме того, я не совсем уверен, почему пытаюсь преобразовать довольно простой процедурный алгоритм в рекурсивный?
обратите внимание, что если вас интересует производительность, то работа с ограниченной точностью (как правило, требуется "двойной", "float",... выходной) на самом деле не имеет смысла, так как очевидный ответ в таком случае просто жестко закодировать значение.
Что такое PI? Окружность круга, деленная на его диаметр.
в компьютерной графике вы можете построить / нарисовать круг с центром в 0,0 от начальной точки x, y, следующая точка x', y' можно найти с помощью простой формулы: x '= x + y / h: y' = y - x' / H
h обычно является степенью 2, так что деление можно легко сделать со сдвигом (или вычитанием из показателя на двойнике). h также хочет быть радиусом r вашего круга. Легкая точка отсчета быть x = r, y = 0, а затем считать c число шагов до x
рекурсия на любую большую глубину обычно непрактична для коммерческой программы, но хвостовая рекурсия позволяет алгоритму выражаться рекурсивно, а реализована как цикл. Рекурсивные алгоритмы поиска иногда могут быть реализованы с использованием очереди, а не стека процесса, поиск должен вернуться из тупика и принять другой путь - эти точки возврата можно поместить в очередь, и несколько процессов могут отменить очередь точек и попробовать другие пути.
вычислить следующим образом:
x = 1 - 1/3 + 1/5 - 1/7 + 1/9 (... etc as far as possible.)
PI = x * 4
У вас есть Pi !!!
Это самый простой способ я знаю.
значение PI медленно сходится к фактическому значению Pi (3.141592165......). Если вы повторяете больше раз, тем лучше.
вот хороший подход (от основная запись Википедии на pi); он сходится гораздо быстрее, чем простая формула, рассмотренная выше, и вполне поддается рекурсивному решению, если ваше намерение состоит в том, чтобы преследовать рекурсию как учебное упражнение. (Предполагая, что вы после опыта обучения, я не даю никакого фактического кода.)
базовая формула такая же, как и выше, но этот подход усредняет частичные суммы для ускорения конвергенция.
определите функцию двух параметров, pie (h, w), такую, что:
pie(0,1) = 4/1
pie(0,2) = 4/1 - 4/3
pie(0,3) = 4/1 - 4/3 + 4/5
pie(0,4) = 4/1 - 4/3 + 4/5 - 4/7
... and so on
Итак, ваша первая возможность изучить рекурсию-это закодировать это" горизонтальное "вычисление по мере увеличения параметра "ширина" (для "высоты" нуля).
затем добавьте второе измерение с этой формулой:
pie(h, w) = (pie(h-1,w) + pie(h-1,w+1)) / 2
, который используется, конечно, только для значений H больше нуля.
хорошая вещь об этом алгоритме заключается в том, что вы можете легко глумиться он с электронной таблицей, чтобы проверить ваш код, как вы исследуете результаты, полученные постепенно больших параметров. К тому времени, когда вы вычислите pie(10,10), у вас будет приблизительное значение для pi, которое достаточно хорошо для большинства инженерных целей.
Enumerable.Range(0, 100000000).Aggregate(0d, (tot, next) => tot += Math.Pow(-1d, next)/(2*next + 1)*4)
using System;
namespace Strings
{
class Program
{
static void Main(string[] args)
{
/* decimal pie = 1;
decimal e = -1;
*/
var stopwatch = new System.Diagnostics.Stopwatch();
stopwatch.Start(); //added this nice stopwatch start routine
//leibniz formula in C# - code written completely by Todd Mandell 2014
/*
for (decimal f = (e += 2); f < 1000001; f++)
{
e += 2;
pie -= 1 / e;
e += 2;
pie += 1 / e;
Console.WriteLine(pie * 4);
}
decimal finalDisplayString = (pie * 4);
Console.WriteLine("pie = {0}", finalDisplayString);
Console.WriteLine("Accuracy resulting from approximately {0} steps", e/4);
*/
// Nilakantha formula - code written completely by Todd Mandell 2014
// π = 3 + 4/(2*3*4) - 4/(4*5*6) + 4/(6*7*8) - 4/(8*9*10) + 4/(10*11*12) - (4/(12*13*14) etc
decimal pie = 0;
decimal a = 2;
decimal b = 3;
decimal c = 4;
decimal e = 1;
for (decimal f = (e += 1); f < 100000; f++)
// Increase f where "f < 100000" to increase number of steps
{
pie += 4 / (a * b * c);
a += 2;
b += 2;
c += 2;
pie -= 4 / (a * b * c);
a += 2;
b += 2;
c += 2;
e += 1;
}
decimal finalDisplayString = (pie + 3);
Console.WriteLine("pie = {0}", finalDisplayString);
Console.WriteLine("Accuracy resulting from {0} steps", e);
stopwatch.Stop();
TimeSpan ts = stopwatch.Elapsed;
Console.WriteLine("Calc Time {0}", ts);
Console.ReadLine();
}
}
}
public static string PiNumberFinder(int digitNumber)
{
string piNumber = "3,";
int dividedBy = 11080585;
int divisor = 78256779;
int result;
for (int i = 0; i < digitNumber; i++)
{
if (dividedBy < divisor)
dividedBy *= 10;
result = dividedBy / divisor;
string resultString = result.ToString();
piNumber += resultString;
dividedBy = dividedBy - divisor * result;
}
return piNumber;
}
в любом производственном сценарии я бы заставил вас искать значение до нужного количества десятичных знаков и хранить его как "const" где-то, где ваши классы могут добраться до него.
(Если вы не пишете научное программное обеспечение "Pi"...)
относительно...
... как это сделать с точки зрения обучения.
вы пытаетесь научиться программировать научные методы? или производить производственное программное обеспечение? Я надеюсь, что сообщество видит это как действительный вопрос, а не придурок.
в любом случае, я думаю, что написание собственного Pi-это решенная проблема. Дмитрий показал "математику".ПИ-константа уже. Атакуйте другую проблему в том же пространстве! Перейти на общий Ньютон приближения или что-то скользкое.
@Thomas Kammeyer:
обратите внимание, что Atan(1.0) довольно часто жестко закодирован, поэтому 4*Atan(1.0) на самом деле не является "алгоритмом", если вы вызываете функцию библиотеки Atan (довольно много уже предложенных действительно, заменяя Atan(x) серией (или бесконечным продуктом) для нее, а затем оценивая ее при x=1.
и есть очень мало случаев, когда вам понадобится pi с большей точностью, чем несколько десятков бит (который можно легко закодировать!). Я работал над приложения в математике, где, чтобы вычислить некоторые (довольно сложные) математические объекты (которые были полиномиальными с целыми коэффициентами), мне пришлось делать арифметику на вещественных и комплексных числах (включая вычисление pi) с точностью до нескольких миллионов бит... но это не очень часто "в реальной жизни":)
вы можете посмотреть следующий пример код.
Мне нравится этой статье, что объясняет, как вычислить π на основе расширения ряда Тейлора для арктангенса.
статья начинается с простого предположения, что
Atan (1) = π/4 Радиана
Atan (x) можно итеративно оценить с помощью серии Тейлора
atan (x) = x - x^3/3 + x^5/5 - x^7/7 + x^9/9...
в документе указывается, почему это не особенно эффективно и далее следует ряд логических уточнений в технике. Они также предоставляют образец программы, которая вычисляет π до нескольких тысяч цифр, в комплекте с исходным кодом, включая необходимые математические процедуры бесконечной точности.
следующая ссылка показывает, как вычислить константу pi на основе ее определения как интеграла, которая может быть записана как предел суммирования, это очень интересно: https://sites.google.com/site/rcorcs/posts/calculatingthepiconstant Файл "Pi как Интеграл" объясняет этот метод, используемый в этом посте.
во-первых, обратите внимание, что C# может использовать математику.Поле PI платформы .NET framework:
https://msdn.microsoft.com/en-us/library/system.math.pi(v=vs. 110).aspx
хорошая особенность здесь в том, что это полноточный двойной, который вы можете использовать или сравнивать с вычисленными результатами. Вкладки в этом URL-адресе имеют аналогичные константы для C++, F# и Visual Basic.
чтобы рассчитать больше мест, вы можете написать свой собственный код расширенной точности. Один, что быстро кодировать и достаточно быстро и легко программировать:
Пи = 4 * [4 * равенства arctg (1/5) - равенства arctg (1/239)]
эта формула и многие другие, в том числе некоторые, которые сходятся с удивительно быстрыми темпами, такими как 50 цифр в члене, находятся в Wolfram:
PI (π) можно рассчитать с помощью бесконечные сериалы. Вот два примера:--9-->
Серия Григория-Лейбница:
π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - ...
C# метод :
public static decimal GregoryLeibnizGetPI(int n)
{
decimal sum = 0;
decimal temp = 0;
for (int i = 0; i < n; i++)
{
temp = 4m / (1 + 2 * i);
sum += i % 2 == 0 ? temp : -temp;
}
return sum;
}
Серия Nilakantha:
π = 3 + 4 / (2x3x4) - 4 / (4x5x6) + 4 / (6x7x8) - 4 / (8x9x10) + ...
C# метод:
public static decimal NilakanthaGetPI(int n)
{
decimal sum = 0;
decimal temp = 0;
decimal a = 2, b = 3, c = 4;
for (int i = 0; i < n; i++)
{
temp = 4 / (a * b * c);
sum += i % 2 == 0 ? temp : -temp;
a += 2; b += 2; c += 2;
}
return 3 + sum;
}
входной параметр n для обеих функций представляет число итераций.
серия Nilakantha по сравнению с серией Григория-Лейбница сходится быстрее. Методы могут быть протестированы со следующим кодом:
static void Main(string[] args)
{
const decimal pi = 3.1415926535897932384626433832m;
Console.WriteLine($"PI = {pi}");
//Nilakantha Series
int iterationsN = 100;
decimal nilakanthaPI = NilakanthaGetPI(iterationsN);
decimal CalcErrorNilakantha = pi - nilakanthaPI;
Console.WriteLine($"\nNilakantha Series -> PI = {nilakanthaPI}");
Console.WriteLine($"Calculation error = {CalcErrorNilakantha}");
int numDecNilakantha = pi.ToString().Zip(nilakanthaPI.ToString(), (x, y) => x == y).TakeWhile(x => x).Count() - 2;
Console.WriteLine($"Number of correct decimals = {numDecNilakantha}");
Console.WriteLine($"Number of iterations = {iterationsN}");
//Gregory-Leibniz Series
int iterationsGL = 1000000;
decimal GregoryLeibnizPI = GregoryLeibnizGetPI(iterationsGL);
decimal CalcErrorGregoryLeibniz = pi - GregoryLeibnizPI;
Console.WriteLine($"\nGregory-Leibniz Series -> PI = {GregoryLeibnizPI}");
Console.WriteLine($"Calculation error = {CalcErrorGregoryLeibniz}");
int numDecGregoryLeibniz = pi.ToString().Zip(GregoryLeibnizPI.ToString(), (x, y) => x == y).TakeWhile(x => x).Count() - 2;
Console.WriteLine($"Number of correct decimals = {numDecGregoryLeibniz}");
Console.WriteLine($"Number of iterations = {iterationsGL}");
Console.ReadKey();
}
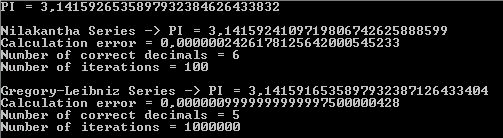
следующий вывод показывает, что серия Nilakantha возвращает шесть правильных десятичных дробей PI с сотней итераций, тогда как серия Григория-Лейбница возвращает пять правильных десятичных дробей PI с миллионом итерации:
мой код может быть протестирован >> здесь
вот хороший способ: Вычислите ряд 1 / x^2 для x от 1 до того, что вы хотите - большее число - лучший результат пирога. Умножьте результат на 6 и на sqrt (). Вот код в C# (только main):
static void Main(string[] args)
{
double counter = 0;
for (double i = 1; i < 1000000; i++)
{
counter = counter + (1 / (Math.Pow(i, 2)));
}
counter = counter * 6;
counter = Math.Sqrt(counter);
Console.WriteLine(counter);
}