Как вычислить расстояния между центроидами и матрицей данных (для алгоритма kmeans)
Я студент кластеризации и R. Чтобы получить лучшее сцепление с обоими, я хотел бы вычислить расстояние между центроидами и моей XY-матрицей для каждой итерации до ее "сходимости". Как я могу решить для шага 2 и 3 с помощью R?
library(fields)
x<-c(3,6,8,1,2,2,6,6,7,7,8,8)
y<-c(5,2,3,5,4,6,1,8,3,6,1,7)
df<-data.frame(x,y) initial matrix
a<-c(3,6,8)
b<-c(5,2,3)
df1<-data.frame(a,b)# initial centroids
вот что я хочу сделать:
- I0
- кластерные объекты на основе минимального расстояния
- определение центроидов на основе кластера в среднем
- повторение с I1
я попробовал функцию kmeans. Но по каким-то причинам он производит те центроиды, которые должны выйти в конце. То есть я определил начало:
start <- matrix(c(3,5,6,2,8,3), 3, byrow = TRUE)
cluster <- kmeans(df,centers = start, iter.max = 1)# one iteration
Kmeans не позволяет мне отслеживать движение центроидов. Поэтому я хотел бы сделать это "вручную", применив Шаг 2 & 3 с помощью R.
1 ответов
ваш главный вопрос заключается в том, как вычислить расстояния между матрицей данных и некоторым набором точек ("центров").
для этого вы можете написать функцию, которая принимает в качестве входных данных матрицу данных и ваш набор точек и возвращает расстояния для каждой строки (точки) в матрице данных для всех "центров".
вот такая функция:
myEuclid <- function(points1, points2) {
distanceMatrix <- matrix(NA, nrow=dim(points1)[1], ncol=dim(points2)[1])
for(i in 1:nrow(points2)) {
distanceMatrix[,i] <- sqrt(rowSums(t(t(points1)-points2[i,])^2))
}
distanceMatrix
}
points1 - это матрица данных с точками в виде строк и размерами в виде столбцов. points2 - это матрица центры (снова точки в виде строк). Первая строка кода задает матрицу ответа (который будет иметь столько строк, сколько строк в матрице данных и столько столбцов, сколько имеется центров). Так что точка i,j в матрице результатов будет расстояние от ith указать jth центр.
затем цикл for повторяется по всем центрам. Для каждого центра вычисляется евклидово расстояние от каждой точки до текущего центра и возвращать результат. Эта строка здесь:sqrt(rowSums(t(t(points1)-points2[i,])^2)) - евклидово расстояние. Проверьте его ближе и посмотрите формулу, Если у вас есть какие-либо проблемы с этим. (транспонирование в основном выполняется, чтобы убедиться, что вычитание выполняется по строкам).
теперь вы также можете реализовать алгоритм k-means:
myKmeans <- function(x, centers, distFun, nItter=10) {
clusterHistory <- vector(nItter, mode="list")
centerHistory <- vector(nItter, mode="list")
for(i in 1:nItter) {
distsToCenters <- distFun(x, centers)
clusters <- apply(distsToCenters, 1, which.min)
centers <- apply(x, 2, tapply, clusters, mean)
# Saving history
clusterHistory[[i]] <- clusters
centerHistory[[i]] <- centers
}
list(clusters=clusterHistory, centers=centerHistory)
}
как вы можете видеть, это также очень простая функция-она принимает матрицу данных, центры, вашу функцию расстояния (определенную выше) и количество разыскиваемых повторения.
кластеры определяются путем назначения ближайшего центра для каждой точки. И центры обновляются как среднее значение точек, назначенных этому центру. Который является основным алгоритмом k-средних).
давайте попробуем. Определите некоторые случайные точки (в 2d, поэтому количество столбцов = 2)
mat <- matrix(rnorm(100), ncol=2)
выбрать 5 случайных точек из этой матрицы в качестве исходных центров:
centers <- mat[sample(nrow(mat), 5),]
Теперь запустите алгоритм:
theResult <- myKmeans(mat, centers, myEuclid, 10)
здесь центры в 10-й итерации:
theResult$centers[[10]]
[,1] [,2]
1 -0.1343239 1.27925285
2 -0.8004432 -0.77838017
3 0.1956119 -0.19193849
4 0.3886721 -1.80298698
5 1.3640693 -0.04091114
сравните это с реализованной kmeans функция:
theResult2 <- kmeans(mat, centers, 10, algorithm="Forgy")
theResult2$centers
[,1] [,2]
1 -0.1343239 1.27925285
2 -0.8004432 -0.77838017
3 0.1956119 -0.19193849
4 0.3886721 -1.80298698
5 1.3640693 -0.04091114
работает нормально. Однако наша функция отслеживает итерации. Мы можем построить прогресс в течение первых 4 итераций следующим образом:
par(mfrow=c(2,2))
for(i in 1:4) {
plot(mat, col=theResult$clusters[[i]], main=paste("itteration:", i), xlab="x", ylab="y")
points(theResult$centers[[i]], cex=3, pch=19, col=1:nrow(theResult$centers[[i]]))
}
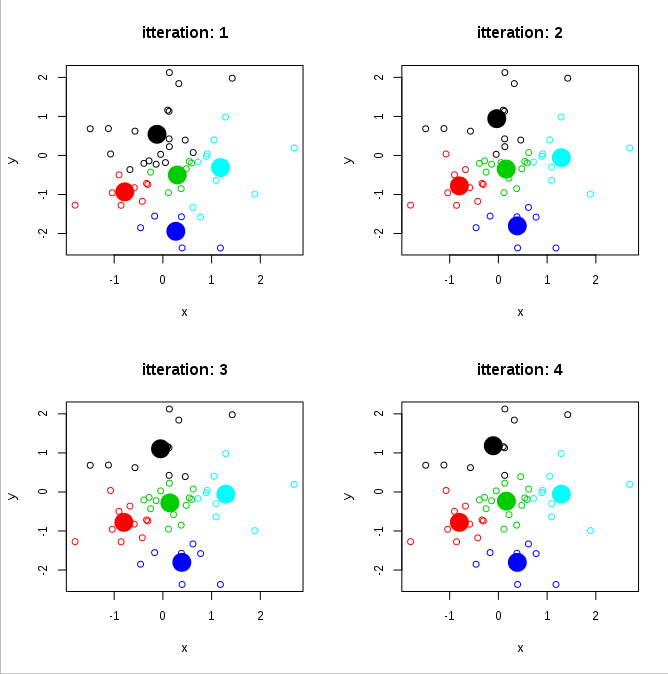
хорошо.
однако этот простой дизайн позволяет гораздо больше. Например, если мы хотим использовать другой вид расстояния (не евклидов), мы можем просто использовать любую функцию, которая принимает данные и центры как входные данные. Вот один для корреляционных расстояний:
myCor <- function(points1, points2) {
return(1 - ((cor(t(points1), t(points2))+1)/2))
}
и мы тогда можем сделать Kmeans на основе тех:
theResult <- myKmeans(mat, centers, myCor, 10)
полученное изображение для 4 итераций выглядит следующим образом:
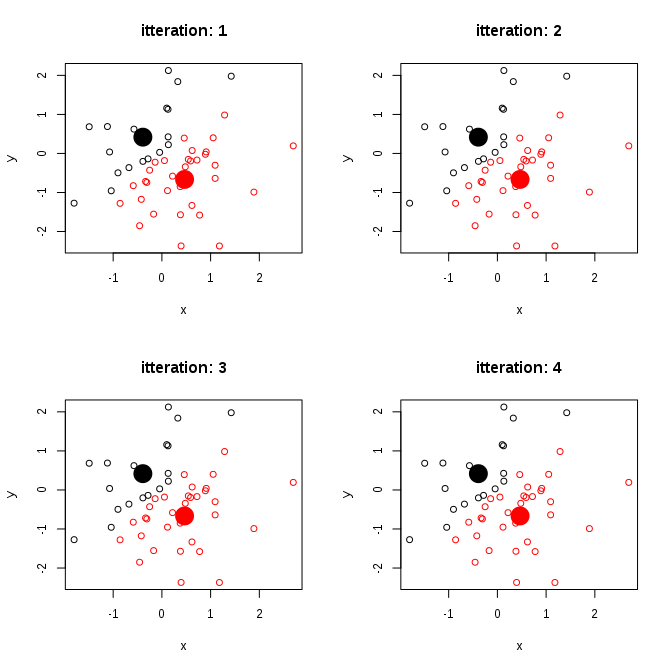
даже ты мы указали 5 кластеров - в конце осталось 2. Это связано с тем, что для 2 измерений корреляция может иметь значения - +1 или -1. Затем при поиске кластеров каждая точка get назначается один центр, даже если он имеет одинаковое расстояние до нескольких центров-выбирается первый.
в любом случае, теперь это выходит за рамки. Суть в том, что существует много возможных метрик расстояния, и одна простая функция позволяет использовать любое расстояние и отслеживать результаты по итерациям.
