Как выполнить билинейную интерполяцию по значениям RGB?
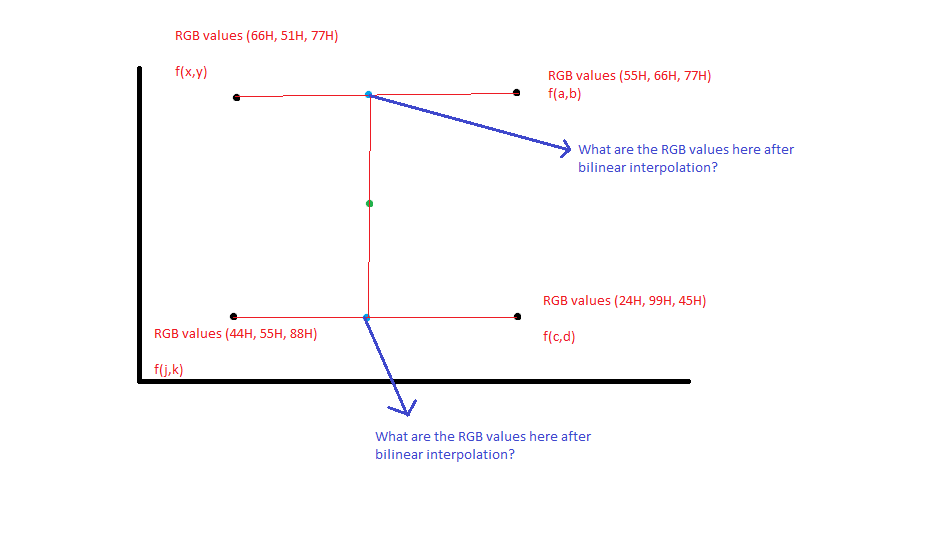
учитывая координаты черного пикселя, я мог бы интерполировать значения координат синего пикселя с помощью математического уравнения y = mx + c. Но как насчет новых значений пикселей RGB? Как я могу получить средневзвешенное значение RGB для синих пикселей, учитывая, что значения RGB черного пикселя приведены как таковые на рисунке?
любая помощь очень ценится. Спасибо заранее.
3 ответов
вы интерполируете значения независимо, выполняя расчет каждый для R, G и B. Например, интерполируя половину между (200,50,10) и (0,0,0) выходами (100,25,5).
(это может занять много времени. Я постараюсь быть кратким, в этом случае мне, вероятно, придется вернуться к моему ответу, чтобы ответить на вопросы.) Интерполяция цветового пространства в RGB часто использует трилинейную интерполяцию, которая может быть построена поверх пары билинейных интерполяций. Но нет необходимости использовать трилинейную интерполяцию. На самом деле, другие интерполанты часто лучше, например, симплициальный (или тетраэдрический) интерполант обычно предпочтительнее по целому ряду причин трилинейный. Существует несколько таких тетраэдрических рассечений решетки, которые можно использовать. Одним достаточно стандартен. (Я не буду вдаваться в подробности, по крайней мере пока.) Кроме того, нет причин, по которым нужно интерполировать в RGB вместо некоторого другого пространства, хотя можно утверждать, что RGB имеет свои собственные особые проблемы, обычно вокруг интерполяции нейтралов и близких нейтралов.
характеристика, относящаяся к RGB и интерполяции, заключается в том, что определяется нейтраль в качестве точки, такой, что R=G=B. трилинейный интерполант будет иметь максимальную ошибку вдоль этой нейтральной оси, и он обычно будет иметь характерную (зубчатую) форму для ошибок вдоль нейтрального пути через цветовое пространство.
Итак, как мы интерполируем в 3-d? Я предположу, что один интерполируется в регулярной решетке точек в цветовом пространстве. В этом случае можно определить куб, содержащий любую точку. Если вы интерполируете внутри рассеянного набора точек, то простейшим решением обычно является построение триангуляции этих точек, а затем выполнение симплициальной (линейной) интерполяции внутри любого заданного тетраэдра. Интерполяторы более высокого порядка здесь проблематичны, так как они могут вызвать проблемы с цветом в некоторых обстоятельствах. Например, не хотелось бы видеть развороты вдоль градиентов. Это может произойти, поскольку звон является серьезной проблемой с интерполяторами на основе сплайнов в областях с относительно высокой кривизной. И если есть отображение гаммы, то такие переходы, безусловно, будут проблемой. Даже если нет необходимости в отображении гаммы, все еще есть проблемы гаммы, которые необходимо решить.
существует несколько способов построения триангуляций доменов из рассеянных данных. Альфа-формы основаны на триангуляции Делоне и являются разумным выбором. Но предполагая, что у вас есть регулярная решетка и вы хотите сделать трилинейную интерполяцию, задача сводится к интерполяции внутри простого Куба в 3-D.
отметим, что трехлинейные интерполяция на самом деле не является линейной интерполяцией, как и билинейная интерполяция. Эти схемы линейны только вдоль осей решетки, но по любому другому пути через цветовое пространство они имеют полиномиальный характер. Таким образом, трилинейный интерполант покажет поведение кубического полинома по главной диагонали или по большинству общих путей через куб. Мы можем убедить себя, что трилинейная интерполяция не является истинно линейной, поскольку есть 8 точек, которые мы интерполируем между. в 3-д, 4 очка определить подлинно линейного интерполятора, как функции этих независимых переменных, но у нас 8 очков, которые определяют Куба. То есть мы будем рассматривать отображение из одного пространства RGB в другое как действительно 3 независимых отображения, таким образом, RGB --> UVW (я выбрал UVW здесь, чтобы представить некоторое общее другое цветовое пространство, которое может быть или не быть RGB по характеру.)
фокус в том, что мы строим трилинейный интерполятор, интерполируя между парой билинейных интерполяторов. Мы постройте эти билинейные интерполяторы путем линейной интерполяции между парой точек вдоль одного края, а затем выполните третью интерполяцию между ними. Таким образом, мы можем рассматривать трилинейный интерполятор как состоящий из 7 простых линейных интерполяций. Интересно, что можно показать, что не имеет значения, по каким осям мы сначала делаем интерполяции. Таким образом, мы можем сначала интерполировать вдоль осей R, затем B, затем G или выбрать любой другой порядок-трилинейный интерполант будет уникальным и идентично для любого выбранного заказа. (То же самое верно и для билинейного интерполятора.)
хитрость в том, как мы делаем линейную интерполяцию между двумя триадами точек? Во-первых, нам нужно определить, где на отрезке линии между этими точками мы лежим. Например, рассмотрим две точки в нашем цветовом пространстве, которые лежат вдоль Красного (R) ребра Куба. Я буду использовать те же значения, которые вы показали для этих точек, таким образом:
Q1 = [66, 51, 77]
Q2 = [55, 66, 77]
это значения, которые мы будем интерполировать между, по существу, выход нашего отображения, но нам также нужно знать, где эти точки лежат во входном пространстве RGB. Поэтому предположим, что эти координаты, основанные на координатах куба, из которого они пришли, являются:
P1 = [0, 0, 0]
P2 = [1, 0, 0]
это единичный куб в 3-d, как я его написал, поэтому другие точки будут лежать в
P3 = [0, 1, 0]
P4 = [1, 1, 0]
P5 = [0, 0, 1]
P6 = [1, 0, 1]
P7 = [0, 1, 1]
P8 = [1, 1, 1]
конечно, любой общий куб также работает, и нет причин для того, чтобы он был истинным кубом. Любая 3-d правая, прямоугольная 4-сторонняя призма будет работать и здесь. Вы можете всегда преобразуйте вещи в единичный куб.
теперь предположим, что мы хотим интерполировать вдоль этого края Куба между P1 и P2 в область, определенную Q1 и Q2? Выбери какую-нибудь точку вдоль этого края. Вы можете видеть, что только R изменяется вдоль этого края между этими точками, поэтому мы заботимся только о значении R в точке, в которой мы интерполируем. Подумайте об этом с точки зрения процента расстояния вдоль края. Интерполяция-это просто средневзвешенное значение двух точек, а линейная комбинация. Таким образом, для точки с красным значением r вдоль края от 0 до 1 в красном канале наша интерполяция будет
Q(r) = Q1*(1-r) + Q2*r
как вы можете видеть, когда r равен 1/2, таким образом, на полпути вдоль края, наш интерполятор уменьшится до
Q(1/2,0,0) = (Q1 + Q2)/2
логически, значение средней точки будет средним из двух конечных точек. Интерполяция для каждого выходного канала выполняется независимо.
Q(1/2,0,0) = ([66, 51, 77] + [55, 66, 77])/2 = [60.5, 58.5, 77]
работает ли это для восстановления конечных точек? Конечно делает. Когда r = 0 или r = 1, Вы можете видеть, что он возвращает точно соответствующий Q1 или Q2.
опять же, вы делаете эту интерполяцию вдоль каждого из четырех красных краев для трилинейного интерполятора. Затем вы делаете еще две интерполяции, возможно, вдоль зеленых краев четырех результатов, которые мы получили выше. И, наконец, сделать один более интерполяции вдоль синей кромки, чтобы получить трехлинейный интерполятора. Опять же, не имеет значения, в каком порядке вы выбираете оси интерполяции. Результат будет математически то же самое.
вы остановились на билинейной интерполяции, тогда есть три такие линейные интерполяции. Да, это правда, что интерполятора билинейной или трехлинейной интерполятора также может быть сделано как взвешенная сумма всех 4 (или 8) углов прямоугольника (или куб). Это можно оставить на будущее.
/*
resize an image using bilinear interpolation
*/
void bilerp(unsigned char *dest, int dwidth, int dheight, unsigned char *src, int swidth, int sheight)
{
float a, b;
float red, green, blue, alpha;
float dx, dy;
float rx, ry;
int x, y;
int index0, index1, index2, index3;
dx = ((float) swidth)/dwidth;
dy = ((float) sheight)/dheight;
for(y=0, ry = 0;y<dheight-1;y++, ry += dy)
{
b = ry - (int) ry;
for(x=0, rx = 0;x<dwidth-1;x++, rx += dx)
{
a = rx - (int) rx;
index0 = (int)ry * swidth + (int) rx;
index1 = index0 + 1;
index2 = index0 + swidth;
index3 = index0 + swidth + 1;
red = src[index0*4] * (1.0f-a)*(1.0f-b);
green = src[index0*4+1] * (1.0f-a)*(1.0f-b);
blue = src[index0*4+2] * (1.0f-a)*(1.0f-b);
alpha = src[index0*4+3] * (1.0f-a)*(1.0f-b);
red += src[index1*4] * (a)*(1.0f-b);
green += src[index1*4+1] * (a)*(1.0f-b);
blue += src[index1*4+2] * (a)*(1.0f-b);
alpha += src[index1*4+3] * (a)*(1.0f-b);
red += src[index2*4] * (1.0f-a)*(b);
green += src[index2*4+1] * (1.0f-a)*(b);
blue += src[index2*4+2] * (1.0f-a)*(b);
alpha += src[index2*4+3] * (1.0f-a)*(b);
red += src[index3*4] * (a)*(b);
green += src[index3*4+1] * (a)*(b);
blue += src[index3*4+2] * (a)*(b);
alpha += src[index3*4+3] * (a)*(b);
red = red < 0 ? 0 : red > 255 ? 255 : red;
green = green < 0 ? 0 : green > 255 ? 255 : green;
blue = blue < 0 ? 0 : blue > 255 ? 255 : blue;
alpha = alpha < 0 ? 0 : alpha > 255 ? 255 : alpha;
dest[(y*dwidth+x)*4] = (unsigned char) red;
dest[(y*dwidth+x)*4+1] = (unsigned char) green;
dest[(y*dwidth+x)*4+2] = (unsigned char) blue;
dest[(y*dwidth+x)*4+3] = (unsigned char) alpha;
}
index0 = (int)ry * swidth + (int) rx;
index1 = index0;
index2 = index0 + swidth;
index3 = index0 + swidth;
red = src[index0*4] * (1.0f-a)*(1.0f-b);
green = src[index0*4+1] * (1.0f-a)*(1.0f-b);
blue = src[index0*4+2] * (1.0f-a)*(1.0f-b);
alpha = src[index0*4+3] * (1.0f-a)*(1.0f-b);
red += src[index1*4] * (a)*(1.0f-b);
green += src[index1*4+1] * (a)*(1.0f-b);
blue += src[index1*4+2] * (a)*(1.0f-b);
alpha += src[index1*4+3] * (a)*(1.0f-b);
red += src[index2*4] * (1.0f-a)*(b);
green += src[index2*4+1] * (1.0f-a)*(b);
blue += src[index2*4+2] * (1.0f-a)*(b);
alpha += src[index2*4+3] * (1.0f-a)*(b);
red += src[index3*4] * (a)*(b);
green += src[index3*4+1] * (a)*(b);
blue += src[index3*4+2] * (a)*(b);
alpha += src[index3*4+3] * (a)*(b);
red = red < 0 ? 0 : red > 255 ? 255 : red;
green = green < 0 ? 0 : green > 255 ? 255 : green;
blue = blue < 0 ? 0 : blue > 255 ? 255 : blue;
alpha = alpha < 0 ? 0 : alpha > 255 ? 255 : alpha;
dest[(y*dwidth+x)*4] = (unsigned char) red;
dest[(y*dwidth+x)*4+1] = (unsigned char) green;
dest[(y*dwidth+x)*4+2] = (unsigned char) blue;
dest[(y*dwidth+x)*4+3] = (unsigned char) alpha;
}
index0 = (int)ry * swidth + (int) rx;
index1 = index0;
index2 = index0 + swidth;
index3 = index0 + swidth;
for(x=0, rx = 0;x<dwidth-1;x++, rx += dx)
{
a = rx - (int) rx;
index0 = (int)ry * swidth + (int) rx;
index1 = index0 + 1;
index2 = index0;
index3 = index0;
red = src[index0*4] * (1.0f-a)*(1.0f-b);
green = src[index0*4+1] * (1.0f-a)*(1.0f-b);
blue = src[index0*4+2] * (1.0f-a)*(1.0f-b);
alpha = src[index0*4+3] * (1.0f-a)*(1.0f-b);
red += src[index1*4] * (a)*(1.0f-b);
green += src[index1*4+1] * (a)*(1.0f-b);
blue += src[index1*4+2] * (a)*(1.0f-b);
alpha += src[index1*4+3] * (a)*(1.0f-b);
red += src[index2*4] * (1.0f-a)*(b);
green += src[index2*4+1] * (1.0f-a)*(b);
blue += src[index2*4+2] * (1.0f-a)*(b);
alpha += src[index2*4+3] * (1.0f-a)*(b);
red += src[index3*4] * (a)*(b);
green += src[index3*4+1] * (a)*(b);
blue += src[index3*4+2] * (a)*(b);
alpha += src[index3*4+3] * (a)*(b);
red = red < 0 ? 0 : red > 255 ? 255 : red;
green = green < 0 ? 0 : green > 255 ? 255 : green;
blue = blue < 0 ? 0 : blue > 255 ? 255 : blue;
alpha = alpha < 0 ? 0 : alpha > 255 ? 255 : alpha;
dest[(y*dwidth+x)*4] = (unsigned char) red;
dest[(y*dwidth+x)*4+1] = (unsigned char) green;
dest[(y*dwidth+x)*4+2] = (unsigned char) blue;
dest[(y*dwidth+x)*4+3] = (unsigned char) alpha;
}
dest[(y*dwidth+x)*4] = src[((sheight-1)*swidth+swidth-1)*4];
dest[(y*dwidth+x)*4+1] = src[((sheight-1)*swidth+swidth-1)*4+1];
dest[(y*dwidth+x)*4+2] = src[((sheight-1)*swidth+swidth-1)*4+2];
dest[(y*dwidth+x)*4+3] = src[((sheight-1)*swidth+swidth-1)*4+3];
}
код, который поддерживается здесь
https://github.com/MalcolmMcLean/babyxrc/blob/master/src/resize.c
