Как выполнить нелинейную оптимизацию с scipy / numpy или sympy?
Я пытаюсь найти оптимальное решение следующей системы уравнений в Python:
(x-x1)^2 + (y-y1)^2 - r1^2 = 0
(x-x2)^2 + (y-y2)^2 - r2^2 = 0
(x-x3)^2 + (y-y3)^2 - r3^2 = 0
учитывая значения точки (x, y) и радиуса (r):
x1, y1, r1 = (0, 0, 0.88)
x2, y2, r2 = (2, 0, 1)
x3, y3, r3 = (0, 2, 0.75)
каков наилучший способ найти оптимальное решение для точки (x ,y)
Используя приведенный выше пример, это будет:
~ (1, 1)
4 ответов
если я правильно понял ваш вопрос, я думаю это то, что вам нужно:
from scipy.optimize import minimize
import numpy as np
def f(coord,x,y,r):
return np.sum( ((coord[0] - x)**2) + ((coord[1] - y)**2) - (r**2) )
x = np.array([0, 2, 0])
y = np.array([0, 0, 2])
r = np.array([.88, 1, .75])
# initial (bad) guess at (x,y) values
initial_guess = np.array([100,100])
res = minimize(f,initial_guess,args = [x,y,r])
что дает:
>>> print res.x
[ 0.66666666 0.66666666]
вы также можете попробовать метод наименьших квадратов, который ожидает целевую функцию, возвращающую вектор. Он хочет минимизировать сумму квадратов этого вектора. Используя наименьшие квадраты, ваша целевая функция будет выглядеть так:
def f2(coord,args):
x,y,r = args
# notice that we're returning a vector of dimension 3
return ((coord[0]-x)**2) + ((coord[1] - y)**2) - (r**2)
и вы бы минимизировать его как Итак:
from scipy.optimize import leastsq
res = leastsq(f2,initial_guess,args = [x,y,r])
что дает:
>>> print res[0]
>>> [ 0.77961518 0.85811473]
это в основном то же самое, что и использование minimize и переписывание исходной целевой функции как:
def f(coord,x,y,r):
vec = ((coord[0]-x)**2) + ((coord[1] - y)**2) - (r**2)
# return the sum of the squares of the vector
return np.sum(vec**2)
это дает:
>>> print res.x
>>> [ 0.77958326 0.8580965 ]
отметим, что args обрабатываются немного по-разному с leastsq, и что структуры данных, возвращаемые двумя функциями, также различны. См. документацию для scipy.optimize.minimize и scipy.optimize.leastsq дополнительные подробности.
посмотреть scipy.optimize документация для дополнительных опций оптимизации.
я заметил, что код в принятом решении больше не работает... Я думаю, может быть scipy.optimize изменился его интерфейс, так как ответ был опубликован. Я могу ошибаться. Несмотря на это, я поддерживаю предложение использовать алгоритмы в scipy.optimize, и принятый ответ демонстрирует, как (или сделал в одно время, если интерфейс изменился).
я добавляю дополнительный ответ здесь, просто чтобы предложить альтернативный пакет, который использует scipy.optimize алгоритмы в ядре, но гораздо надежнее для ограниченной оптимизации. Пакет mystic. Одним из больших улучшений является то, что mystic дает ограниченное глобальные оптимизация.
во-первых, вот ваш пример, сделанный очень похоже на scipy.optimize.minimize путь, но с использованием глобального оптимизатора.
from mystic import reduced
@reduced(lambda x,y: abs(x)+abs(y)) #choice changes answer
def objective(x, a, b, c):
x,y = x
eqns = (\
(x - a[0])**2 + (y - b[0])**2 - c[0]**2,
(x - a[1])**2 + (y - b[1])**2 - c[1]**2,
(x - a[2])**2 + (y - b[2])**2 - c[2]**2)
return eqns
bounds = [(None,None),(None,None)] #unnecessary
a = (0,2,0)
b = (0,0,2)
c = (.88,1,.75)
args = a,b,c
from mystic.solvers import diffev2
from mystic.monitors import VerboseMonitor
mon = VerboseMonitor(10)
result = diffev2(objective, args=args, x0=bounds, bounds=bounds, npop=40, \
ftol=1e-8, disp=False, full_output=True, itermon=mon)
print result[0]
print result[1]
С результатами в таком виде:
Generation 0 has Chi-Squared: 38868.949133
Generation 10 has Chi-Squared: 2777.470642
Generation 20 has Chi-Squared: 12.808055
Generation 30 has Chi-Squared: 3.764840
Generation 40 has Chi-Squared: 2.996441
Generation 50 has Chi-Squared: 2.996441
Generation 60 has Chi-Squared: 2.996440
Generation 70 has Chi-Squared: 2.996433
Generation 80 has Chi-Squared: 2.996433
Generation 90 has Chi-Squared: 2.996433
STOP("VTRChangeOverGeneration with {'gtol': 1e-06, 'target': 0.0, 'generations': 30, 'ftol': 1e-08}")
[ 0.66667151 0.66666422]
2.99643333334
как уже отмечалось, выбор lambda на reduced влияет на то, какую точку оптимизатор находит, поскольку нет фактическое решение уравнений.
mystic также обеспечивает возможность преобразования символьных уравнений в функцию, где результирующая функция может использоваться как цель или как штрафная функция. Вот та же проблема, но с использованием уравнений в качестве штрафа вместо цели.
def objective(x):
return 0.0
equations = """
(x0 - 0)**2 + (x1 - 0)**2 - .88**2 == 0
(x0 - 2)**2 + (x1 - 0)**2 - 1**2 == 0
(x0 - 0)**2 + (x1 - 2)**2 - .75**2 == 0
"""
bounds = [(None,None),(None,None)] #unnecessary
from mystic.symbolic import generate_penalty, generate_conditions
from mystic.solvers import diffev2
pf = generate_penalty(generate_conditions(equations), k=1e12)
result = diffev2(objective, x0=bounds, bounds=bounds, penalty=pf, \
npop=40, gtol=50, disp=False, full_output=True)
print result[0]
print result[1]
результаты:
[ 0.77958328 0.8580965 ]
3.6473132399e+12
результаты отличаются от предыдущих, потому что примененный штраф отличается от того, что мы применяли ранее в reduced. В mystic, вы можете выбрать, какой штраф вы хотите применить.
было отмечено, что уравнение не имеет решения. Из приведенного выше результата видно, что результат сильно наказывается, так что это хороший признак того, что решения нет. Однако,mystic имеет другой способ, который вы можете увидеть там в решении. Вместо применения более традиционного penalty, что наказывает решение, в котором нарушаются ограничения... mystic предоставляет constraint, который по сути, преобразование ядра, которое удаляет все потенциальные решения, которые не соответствуют константам.
def objective(x):
return 0.0
equations = """
(x0 - 0)**2 + (x1 - 0)**2 - .88**2 == 0
(x0 - 2)**2 + (x1 - 0)**2 - 1**2 == 0
(x0 - 0)**2 + (x1 - 2)**2 - .75**2 == 0
"""
bounds = [(None,None),(None,None)] #unnecessary
from mystic.symbolic import generate_constraint, generate_solvers, simplify
from mystic.symbolic import generate_penalty, generate_conditions
from mystic.solvers import diffev2
cf = generate_constraint(generate_solvers(simplify(equations)))
result = diffev2(objective, x0=bounds, bounds=bounds, \
constraints=cf, \
npop=40, gtol=50, disp=False, full_output=True)
print result[0]
print result[1]
результаты:
[ nan 657.17740835]
0.0
здесь nan по существу указывает, что нет допустимого решения.
к вашему сведению, я автор, поэтому у меня есть некоторые предубеждения. Однако,mystic существует почти столько же, сколько scipy.optimize, является зрелым и имеет более стабильный интерфейс в течение этого периода времени. Дело в том, если вам нужен более гибкий и мощный ограниченный нелинейный оптимизатор, я предлагаю mystic.
эти уравнения можно рассматривать как описывающие все точки на окружности трех кругов в 2D-пространстве. Решение будет заключаться в точках пересечения кругов.
сумма их радиусов окружностей меньше расстояния между их центрами, так что круги не пересекаются. Я проложил круги шкалы ниже:
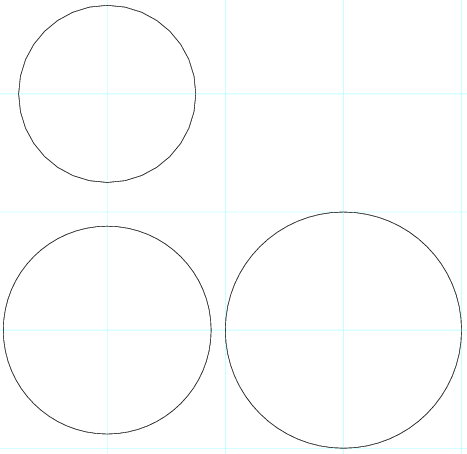
нет точек, удовлетворяющих этой системе уравнений.
Я сделал пример сценария следующим образом. Обратите внимание, что последняя строка найдет оптимальное решение (a, b):
import numpy as np
import scipy as scp
import sympy as smp
from scipy.optimize import minimize
a,b = smp.symbols('a b')
x_ar, y_ar = np.random.random(3), np.random.random(3)
x = np.array(smp.symbols('x0:%d'%np.shape(x_ar)[0]))
y = np.array(smp.symbols('y0:%d'%np.shape(x_ar)[0]))
func = np.sum(a**2+b**2-x*(a+b)+2*y)
print func
my_func = smp.lambdify((x,y), func)
print 1.0/3*my_func(x_ar,y_ar)
ab = smp.lambdify((a,b),my_func(x_ar,x_ar))
print ab(1,2)
def ab_v(x):
return ab(*tuple(x))
print ab_v((1,2))
minimize(ab_v,(0.1,0.1))
выходы :
3*a**2 + 3*b**2 - x0*(a + b) - x1*(a + b) - x2*(a + b) + 2*y0 + 2*y1 + 2*y2
1.0*a**2 - 0.739792011558683*a + 1.0*b**2 - 0.739792011558683*b +0.67394435712335
12.7806239653
12.7806239653
Out[33]:
status: 0
success: True
njev: 3
nfev: 12
hess_inv: array([[1, 0],
[0, 1]])
fun: 3.6178137388030356
x: array([ 0.36989601, 0.36989601])
message: 'Optimization terminated successfully.'
jac: array([ 5.96046448e-08, 5.96046448e-08])
