Как я могу рисовать линии в массивы numpy?
Я хотел бы иметь возможность рисовать линии в массивы numpy, чтобы получить автономные функции для распознавания он-лайн почерка. Это означает, что мне вообще не нужно изображение, но мне нужны некоторые позиции в массиве numpy, на которые будет выглядеть изображение заданного размера.
Я хотел бы иметь возможность указать размер изображения, а затем рисовать штрихи следующим образом:
import module
im = module.new_image(width=800, height=200)
im.add_stroke(from={'x': 123, 'y': 2}, to={'x': 42, 'y': 3})
im.add_stroke(from={'x': 4, 'y': 3}, to={'x': 2, 'y': 1})
features = im.get(x_min=12, x_max=15, y_min=0, y_max=111)
возможно ли что-то простое (желательно непосредственно с numpy / scipy)?
(пожалуйста обратите внимание, что мне нужна интерполяция серой шкалы. Так что features должна быть матрица значений [0, 255].)
3 ответов
спасибо Джо Кингтон за ответ! Я искал skimage.draw.line_aa.
import scipy.misc
import numpy as np
from skimage.draw import line_aa
img = np.zeros((10, 10), dtype=np.uint8)
rr, cc, val = line_aa(1, 1, 8, 4)
img[rr, cc] = val * 255
scipy.misc.imsave("out.png", img)
я наткнулся на этот вопрос, ища решение, и предоставленный ответ решает его довольно хорошо. Однако это не совсем соответствовало моим целям, для которых мне нужно было "тензоризуемое" решение (т. е. реализованное в numpy без явных циклов) и, возможно, с опцией linewidth. Я в конечном итоге реализовал свою собственную версию, и поскольку в конце концов она также довольно быстрее, чем line_aa, я подумал, что могу поделиться ею.
оно приходит в 2 флейворы, С и без linewidth. На самом деле первое не является обобщением второго и не полностью согласуется с line_aa, но для моих целей они просто прекрасны, и на сюжетах они выглядят нормально.
def naive_line(r0, c0, r1, c1):
# The algorithm below works fine if c1 >= c0 and c1-c0 >= abs(r1-r0).
# If either of these cases are violated, do some switches.
if abs(c1-c0) < abs(r1-r0):
# Switch x and y, and switch again when returning.
xx, yy, val = naive_line(c0, r0, c1, r1)
return (yy, xx, val)
# At this point we know that the distance in columns (x) is greater
# than that in rows (y). Possibly one more switch if c0 > c1.
if c0 > c1:
return naive_line(r1, c1, r0, c0)
# We write y as a function of x, because the slope is always <= 1
# (in absolute value)
x = np.arange(c0, c1+1, dtype=float)
y = x * (r1-r0) / (c1-c0) + (c1*r0-c0*r1) / (c1-c0)
valbot = np.floor(y)-y+1
valtop = y-np.floor(y)
return (np.concatenate((np.floor(y), np.floor(y)+1)).astype(int), np.concatenate((x,x)).astype(int),
np.concatenate((valbot, valtop)))
я назвал это "наивным", потому что это очень похоже на наивную реализацию в Википедия, но с некоторым сглаживанием, хотя и не идеально (например, делает очень тонкие диагонали).
взвешенная версия дает гораздо более толстую линию более выраженной анти-алиасинг.
def trapez(y,y0,w):
return np.clip(np.minimum(y+1+w/2-y0, -y+1+w/2+y0),0,1)
def weighted_line(r0, c0, r1, c1, w, rmin=0, rmax=np.inf):
# The algorithm below works fine if c1 >= c0 and c1-c0 >= abs(r1-r0).
# If either of these cases are violated, do some switches.
if abs(c1-c0) < abs(r1-r0):
# Switch x and y, and switch again when returning.
xx, yy, val = weighted_line(c0, r0, c1, r1, w, rmin=rmin, rmax=rmax)
return (yy, xx, val)
# At this point we know that the distance in columns (x) is greater
# than that in rows (y). Possibly one more switch if c0 > c1.
if c0 > c1:
return weighted_line(r1, c1, r0, c0, w, rmin=rmin, rmax=rmax)
# The following is now always < 1 in abs
slope = (r1-r0) / (c1-c0)
# Adjust weight by the slope
w *= np.sqrt(1+np.abs(slope)) / 2
# We write y as a function of x, because the slope is always <= 1
# (in absolute value)
x = np.arange(c0, c1+1, dtype=float)
y = x * slope + (c1*r0-c0*r1) / (c1-c0)
# Now instead of 2 values for y, we have 2*np.ceil(w/2).
# All values are 1 except the upmost and bottommost.
thickness = np.ceil(w/2)
yy = (np.floor(y).reshape(-1,1) + np.arange(-thickness-1,thickness+2).reshape(1,-1))
xx = np.repeat(x, yy.shape[1])
vals = trapez(yy, y.reshape(-1,1), w).flatten()
yy = yy.flatten()
# Exclude useless parts and those outside of the interval
# to avoid parts outside of the picture
mask = np.logical_and.reduce((yy >= rmin, yy < rmax, vals > 0))
return (yy[mask].astype(int), xx[mask].astype(int), vals[mask])
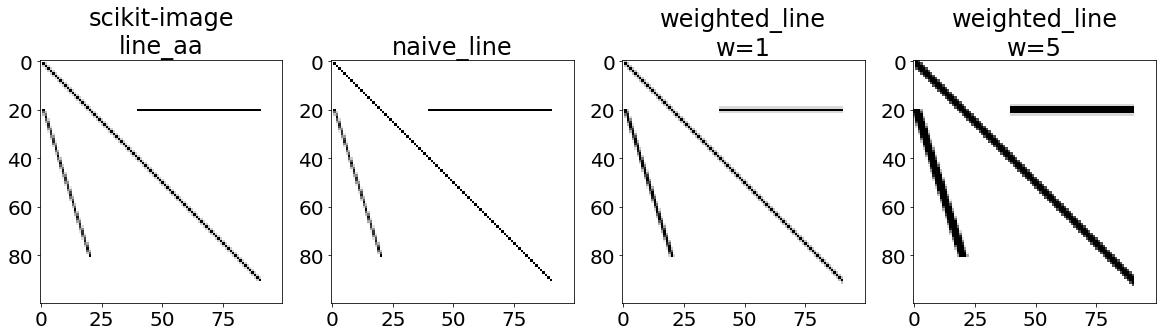
регулировка веса, по общему признанию, довольно произвольна, поэтому любой может настроить это на свой вкус. Rmin и rmax теперь необходимы, чтобы избежать пикселей за пределами изображения. Сравнение:
как вы можете видеть, даже при w=1, weighted_line немного толще, но в некотором роде однородным образом; аналогично, naive_line однородно немного тоньше.
заключительная заметка о бенчмаркинге: на моем машина, бегом!--2--> для различных функций (w=1 для weighted_line) привело к времени 90 МКС для line_aa, 84 МКС для weighted_line (хотя время, конечно, увеличивается с весом) и 18 МКС для naive_line. Опять же для сравнения, переопределение line_aa в чистом Python (вместо Cython, как в пакете) заняло 350 МКС.
Я нашел val * 255 подход в ответе неоптимальный, потому что он, кажется, работает правильно только на черном фоне. Если фон содержит более темные и яркие области, это не кажется совсем правильным:
чтобы он работал правильно на всех фонах, нужно учитывать цвета пикселей,которые покрыты сглаженной линией.
Here is a little demo that builds on the original answer:
from scipy import ndimage
from scipy import misc
from skimage.draw import line_aa
import numpy as np
img = np.zeros((100, 100, 4), dtype = np.uint8) # create image
img[:,:,3] = 255 # set alpha to full
img[30:70, 40:90, 0:3] = 255 # paint white rectangle
rows, cols, weights = line_aa(10, 10, 90, 90) # antialias line
w = weights.reshape([-1, 1]) # reshape anti-alias weights
lineColorRgb = [255, 120, 50] # color of line, orange here
img[rows, cols, 0:3] = (
np.multiply((1 - w) * np.ones([1, 3]),img[rows, cols, 0:3]) +
w * np.array([lineColorRgb])
)
misc.imsave('test.png', img)
самая интересная часть is
np.multiply((1 - w) * np.ones([1, 3]),img[rows, cols, 0:3]) +
w * np.array([lineColorRgb])
где новый цвет вычисляется из исходного цвета изображения и цвета линии с помощью линейной интерполяции с использованием значений из анти-псевдонима weights. Вот результат, оранжевая линия работает над двумя видами фона:
теперь пиксели, которые окружают линию в верхней половине, становятся темный, тогда как пиксели в нижней половине стало ярче.