Какова минимальная стоимость подключения всех островов?
существует сетка размера N x M. Некоторые клетки острова обозначается "0", а остальные вода. Каждая ячейка имеет номер, обозначающий стоимость моста, сделанные на этой камере. Вы должны найти минимальную стоимость, за которую можно подключить все острова. Ячейка соединяется с другой ячейкой, если она разделяет ребро или вершину.
какой алгоритм можно использовать для решения этой проблемы ?
изменить: что может быть используется как подход грубой силы, если значения N, M очень малы, скажем NxM
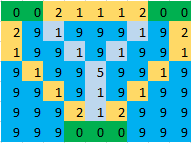
пример: на данном изображении зеленые клетки указывают на острова, синие-на воду, а светло-голубые-на клетки, на которых должен быть сделан мост. Таким образом, для следующего изображения ответ будет 17.

Первоначально я думал о маркировке всех островов как узлов и соединении каждой пары островов кратчайшим мост. Тогда проблема может быть сведена к минимальному связующему дереву, но в этом подходе я пропустил случай, когда ребра перекрываются. , на следующем изображении, кратчайшее расстояние между двумя островами составляет 7(помечено желтым цветом), поэтому при использовании минимальных охватывающих деревьев ответ будет 14, но ответ должен быть 11 (отмечены голубым цветом).
5 ответов
чтобы подойти к этой проблеме, я бы использовал целочисленную структуру программирования и определил три набора переменных решения:
- x_ij: двоичная индикаторная переменная для того, строим ли мы мост в месте расположения воды (i, j).
- y_ijbcn: двоичный индикатор того, является ли местоположение воды (i, j) n^ - м местоположением, связывающим остров b с островом c.
- l_bc: переменная двоичного индикатора для острова b и c напрямую связаны (ака вы можете ходить только по мостовым площадям от b до c).
для стоимости строительства моста c_ij, целевое значение для минимизации -sum_ij c_ij * x_ij. Нам нужно добавить в модель следующие ограничения:
- мы должны обеспечить y_ijbcn переменные являются действительными. Мы всегда можем добраться только до водной площади, если построим там мост, так что
y_ijbcn <= x_ijдля каждого местоположения воды (i, j). Далее,y_ijbc1должно быть равно 0, если (i, j) не граничит с островом b. Наконец, для n > 1,y_ijbcnможет использоваться только в том случае, если на шаге n-1 было использовано соседнее водное местоположение. ОпределениеN(i, j)чтобы быть соседними квадратами воды (i, j), это эквивалентноy_ijbcn <= sum_{(l, m) in N(i, j)} y_lmbc(n-1). - мы должны обеспечить l_bc переменные устанавливаются только в том случае, если B и c связаны. Если мы определим
I(c)чтобы быть местоположениями, граничащими с островом c, это может быть выполнено сl_bc <= sum_{(i, j) in I(c), n} y_ijbcn. - мы должны обеспечить что все острова связаны, прямо или косвенно. Это можно сделать следующим образом: для каждого непустого собственного подмножества s островов требуется, чтобы по крайней мере один остров в S был связан по крайней мере с одним островом в дополнении S, которое мы будем называть S'. В ограничениях мы можем реализовать это, добавив ограничение для каждого непустого множества s размера sum_{b in S} sum_{c in S'} l_bc >= 1.
для экземпляра проблемы с K островами, W вода квадраты и заданная максимальная длина пути N, это смешанная целочисленная модель программирования с O(K^2WN) переменные и O(K^2WN + 2^K) ограничения. Очевидно, что это станет трудноразрешимым, поскольку размер проблемы становится большим, но он может быть разрешим для размеров, которые вас волнуют. Чтобы получить представление о масштабируемости, я реализую его в python с помощью пакета pulp. Давайте начнем с карты меньшего размера 7 x 9 с 3 островами в нижней части вопроса:
import itertools
import pulp
water = {(0, 2): 2.0, (0, 3): 1.0, (0, 4): 1.0, (0, 5): 1.0, (0, 6): 2.0,
(1, 0): 2.0, (1, 1): 9.0, (1, 2): 1.0, (1, 3): 9.0, (1, 4): 9.0,
(1, 5): 9.0, (1, 6): 1.0, (1, 7): 9.0, (1, 8): 2.0,
(2, 0): 1.0, (2, 1): 9.0, (2, 2): 9.0, (2, 3): 1.0, (2, 4): 9.0,
(2, 5): 1.0, (2, 6): 9.0, (2, 7): 9.0, (2, 8): 1.0,
(3, 0): 9.0, (3, 1): 1.0, (3, 2): 9.0, (3, 3): 9.0, (3, 4): 5.0,
(3, 5): 9.0, (3, 6): 9.0, (3, 7): 1.0, (3, 8): 9.0,
(4, 0): 9.0, (4, 1): 9.0, (4, 2): 1.0, (4, 3): 9.0, (4, 4): 1.0,
(4, 5): 9.0, (4, 6): 1.0, (4, 7): 9.0, (4, 8): 9.0,
(5, 0): 9.0, (5, 1): 9.0, (5, 2): 9.0, (5, 3): 2.0, (5, 4): 1.0,
(5, 5): 2.0, (5, 6): 9.0, (5, 7): 9.0, (5, 8): 9.0,
(6, 0): 9.0, (6, 1): 9.0, (6, 2): 9.0, (6, 6): 9.0, (6, 7): 9.0,
(6, 8): 9.0}
islands = {0: [(0, 0), (0, 1)], 1: [(0, 7), (0, 8)], 2: [(6, 3), (6, 4), (6, 5)]}
N = 6
# Island borders
iborders = {}
for k in islands:
iborders[k] = {}
for i, j in islands[k]:
for dx in [-1, 0, 1]:
for dy in [-1, 0, 1]:
if (i+dx, j+dy) in water:
iborders[k][(i+dx, j+dy)] = True
# Create models with specified variables
x = pulp.LpVariable.dicts("x", water.keys(), lowBound=0, upBound=1, cat=pulp.LpInteger)
pairs = [(b, c) for b in islands for c in islands if b < c]
yvals = []
for i, j in water:
for b, c in pairs:
for n in range(N):
yvals.append((i, j, b, c, n))
y = pulp.LpVariable.dicts("y", yvals, lowBound=0, upBound=1)
l = pulp.LpVariable.dicts("l", pairs, lowBound=0, upBound=1)
mod = pulp.LpProblem("Islands", pulp.LpMinimize)
# Objective
mod += sum([water[k] * x[k] for k in water])
# Valid y
for k in yvals:
i, j, b, c, n = k
mod += y[k] <= x[(i, j)]
if n == 0 and not (i, j) in iborders[b]:
mod += y[k] == 0
elif n > 0:
mod += y[k] <= sum([y[(i+dx, j+dy, b, c, n-1)] for dx in [-1, 0, 1] for dy in [-1, 0, 1] if (i+dx, j+dy) in water])
# Valid l
for b, c in pairs:
mod += l[(b, c)] <= sum([y[(i, j, B, C, n)] for i, j, B, C, n in yvals if (i, j) in iborders[c] and B==b and C==c])
# All islands connected (directly or indirectly)
ikeys = islands.keys()
for size in range(1, len(ikeys)/2+1):
for S in itertools.combinations(ikeys, size):
thisSubset = {m: True for m in S}
Sprime = [m for m in ikeys if not m in thisSubset]
mod += sum([l[(min(b, c), max(b, c))] for b in S for c in Sprime]) >= 1
# Solve and output
mod.solve()
for row in range(min([m[0] for m in water]), max([m[0] for m in water])+1):
for col in range(min([m[1] for m in water]), max([m[1] for m in water])+1):
if (row, col) in water:
if x[(row, col)].value() > 0.999:
print "B",
else:
print "-",
else:
print "I",
print ""
это занимает 1,4 секунды для запуска с помощью решателя по умолчанию из пакета pulp (решатель CBC) и выводит правильное решение:
I I - - - - - I I
- - B - - - B - -
- - - B - B - - -
- - - - B - - - -
- - - - B - - - -
- - - - B - - - -
- - - I I I - - -
Далее рассмотрим полную проблему в верхней части вопроса, которая представляет собой сетку 13 x 14 с 7 островами:
water = {(i, j): 1.0 for i in range(13) for j in range(14)}
islands = {0: [(0, 0), (0, 1), (1, 0), (1, 1), (2, 0), (2, 1)],
1: [(9, 0), (9, 1), (10, 0), (10, 1), (10, 2), (11, 0), (11, 1),
(11, 2), (12, 0)],
2: [(0, 7), (0, 8), (1, 7), (1, 8), (2, 7)],
3: [(7, 7), (8, 6), (8, 7), (8, 8), (9, 7)],
4: [(0, 11), (0, 12), (0, 13), (1, 12)],
5: [(4, 10), (4, 11), (5, 10), (5, 11)],
6: [(11, 8), (11, 9), (11, 13), (12, 8), (12, 9), (12, 10), (12, 11),
(12, 12), (12, 13)]}
for k in islands:
for i, j in islands[k]:
del water[(i, j)]
for i, j in [(10, 7), (10, 8), (10, 9), (10, 10), (10, 11), (10, 12),
(11, 7), (12, 7)]:
water[(i, j)] = 20.0
N = 7
решатели MIP часто получают хорошие решения относительно быстро, а затем тратят огромное количество времени, пытаясь доказать оптимальность решения. Используя тот же код решателя, что и выше, программа не завершается в течение 30 минут. Однако вы можете предоставить тайм-аут решателю, чтобы получить приблизительное решение:
mod.solve(pulp.solvers.PULP_CBC_CMD(maxSeconds=120))
это дает решение с объективным значением 17:
I I - - - - - I I - - I I I
I I - - - - - I I - - - I -
I I - - - - - I - B - B - -
- - B - - - B - - - B - - -
- - - B - B - - - - I I - -
- - - - B - - - - - I I - -
- - - - - B - - - - - B - -
- - - - - B - I - - - - B -
- - - - B - I I I - - B - -
I I - B - - - I - - - - B -
I I I - - - - - - - - - - B
I I I - - - - - I I - - - I
I - - - - - - - I I I I I I
чтобы улучшить качество получаемых решений, вы можете использовать коммерческий решатель MIP (это бесплатно, если вы находитесь в Академическом учреждении и, вероятно, не бесплатно в противном случае). Например, вот производительность Gurobi 6.0.4, опять же с 2-минутным ограничением времени (хотя из журнала решений мы читаем, что решатель нашел текущее лучшее решение в течение 7 секунд):
mod.solve(pulp.solvers.GUROBI(timeLimit=120))
это на самом деле находит решение объективной ценности 16, лучше, чем OP смог найти вручную!
I I - - - - - I I - - I I I
I I - - - - - I I - - - I -
I I - - - - - I - B - B - -
- - B - - - - - - - B - - -
- - - B - - - - - - I I - -
- - - - B - - - - - I I - -
- - - - - B - - B B - - - -
- - - - - B - I - - B - - -
- - - - B - I I I - - B - -
I I - B - - - I - - - - B -
I I I - - - - - - - - - - B
I I I - - - - - I I - - - I
I - - - - - - - I I I I I I
эта проблема является вариантом дерева Штайнера под названием взвешенное узлом дерево Штайнера, специализированный определенный класс графов. Компактно, взвешенное узлом дерево Штайнера, учитывая взвешенный узлом неориентированный граф, где некоторые узлы являются терминалами, находит самый дешевый набор узлов, включая все терминалы, которые индуцируют связанный подграф. К сожалению, я не могу найти решателей в некоторых беглых поисках.
чтобы сформулировать как целочисленную программу, сделайте переменную 0-1 для каждого терминальный узел, то для всех подмножеств терминальных узлов, удаление которых из начального графа разъединяет два терминала, требуется, чтобы сумма переменных в подмножестве была не менее 1. Это вызывает слишком много ограничений, поэтому вам придется применять их лениво, используя эффективный алгоритм подключения узлов (в основном max flow) для обнаружения максимально нарушенного ограничения. Извините за отсутствие деталей, но это будет больно реализовать, даже если вы уже знакомы с целочисленное Программирование.
подход грубой силы, в псевдо-коде:
start with a horrible "best" answer
given an nxm map,
try all 2^(n*m) combinations of bridge/no-bridge for each cell
if the result is connected, and better than previous best, store it
return best
в C++, это может быть записано как
// map = linearized map; map[x*n + y] is the equivalent of map2d[y][x]
// nm = n*m
// bridged = true if bridge there, false if not. Also linearized
// nBridged = depth of recursion (= current bridge being considered)
// cost = total cost of bridges in 'bridged'
// best, bestCost = best answer so far. Initialized to "horrible"
void findBestBridges(char map[], int nm,
bool bridged[], int nBridged, int cost, bool best[], int &bestCost) {
if (nBridged == nm) {
if (connected(map, nm, bridged) && cost < bestCost) {
memcpy(best, bridged, nBridged);
bestCost = best;
}
return;
}
if (map[nBridged] != 0) {
// try with a bridge there
bridged[nBridged] = true;
cost += map[nBridged];
// see how it turns out
findBestBridges(map, nm, bridged, nBridged+1, cost, best, bestCost);
// remove bridge for further recursion
bridged[nBridged] = false;
cost -= map[nBridged];
}
// and try without a bridge there
findBestBridges(map, nm, bridged, nBridged+1, cost, best, bestCost);
}
после первого вызова (я предполагаю, что вы преобразуете свои 2d-карты в массивы 1d для удобства копирования),bestCost будет содержать стоимость лучшего ответа, и best будет содержать шаблон мостов, который дает его. Это, однако, очень медленно.
оптимизация:
- путем использование "предела моста", и запустив алгоритм увеличения максимального числа мостов, можно найти минимальные ответы, не исследуя все дерево. Нахождение 1-мостового ответа, если бы он существовал, было бы O(nm) вместо O(2^nm) - резкое улучшение.
- вы можете избежать поиска (остановив рекурсию; это также называется "обрезка"), как только вы превысили
bestCost, потому что нет смысла продолжать смотреть потом. Если не станет лучше, не копай дальше. - вышеуказанные работы обрезки лучше, если вы посмотрите на "хороших" кандидатов, прежде чем смотреть на "плохих" (как это, все ячейки просматриваются слева направо, сверху вниз). Хорошей эвристикой было бы рассматривать ячейки, близкие к нескольким несвязанным компонентам, как более приоритетные, чем ячейки, которые не являются. Однако, как только вы добавляете эвристику, ваш поиск начинает напоминать A* (и вам тоже нужна какая-то приоритетная очередь).
- дубликатов мостов и мостов в никуда следует избегать. Любой мост, который не отключает островную сеть, если удален, является избыточным.
общий алгоритм поиска, такие как A* позволяет значительно ускорить поиск, хотя поиск лучшей эвристики-непростая задача. Для более проблемного подхода, используя существующие результаты на деревьев Штейнера, как предложил @Gassa, это путь. Заметим, однако, что задача построения деревьев Штайнера на ортогональных сетках NP-полная, согласно этому бумага гари и Джонсона.
если "достаточно хорошо" достаточно, генетический алгоритм, вероятно, может быстро найти приемлемые решения, если вы добавите несколько ключевых эвристик относительно предпочтительного размещения моста.
учитывая, что эта проблема имеет место в сетке, и у вас есть хорошо определенные параметры, я бы подошел к проблеме с систематическим устранением проблемного пространства путем создания минимального остовного дерева. При этом для меня имеет смысл, если вы подойдете к этой проблеме с алгоритмом Prim.
к сожалению, теперь вы сталкиваетесь с проблемой абстрагирования сетки для создания набора узлов и ребер... следовательно, реальная проблема этого поста как сконвертировать мой n x m сетка в {V} и {E}?
этот процесс преобразования, на первый взгляд, вероятно, NP-жесткий из-за огромного количества возможных комбинаций (предположим, что все расходы на водные пути идентичны). Чтобы обрабатывать экземпляры, где пути перекрываются, вы должны рассмотреть возможность создания виртуальный остров.
когда это будет сделано, запустите алгоритм Prim, и вы должны прийти к оптимальному решению.
Я не верю, что динамическое программирование можно эффективно работать здесь потому что нет наблюдаемого принципа оптимальности. Если мы найдем минимальную стоимость между двумя островами, это не обязательно означает, что мы можем найти минимальную стоимость между этими двумя и третьим островом или другим подмножеством островов, которые будут (по моему определению, чтобы найти MST через Prim) связаны.
Если вы хотите, чтобы код (псевдо или иначе) преобразовал вашу сетку в набор {V} и {E}, пожалуйста, пришлите мне личное сообщение, и я посмотрю на сращивание реализация.
Я согласен, что это проблема коммивояжера, но ее можно грубо принудить с n=7. Рассчитайте минимальный путь затрат между каждым островом, и у вас будет только n (n-1)/2 решения = 21 вычисление
