Косинусное расстояние как векторная функция расстояния для k-средних
у меня есть граф из N вершин, где каждая вершина представляет место. Также у меня есть векторы, по одному на пользователя, каждый из N коэффициентов, где значение коэффициента-продолжительность в секундах, проведенных в соответствующем месте или 0, если это место не было посещено.
Е. Г. для графа:
вектор:
v1 = {100, 50, 0 30, 0}
означало бы, что мы потратили:
100secs at vertex 1
50secs at vertex 2 and
30secs at vertex 4
(вершины 3 & 5, где не побывал, таким образом, 0С).
Я хочу запустить кластеризацию k-means, и я выбрал cosine_distance = 1 - cosine_similarity как метрика для расстояний, где формула для cosine_similarity - это:
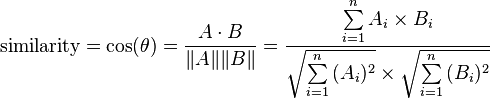
как рассказали здесь.
но я заметил следующее. Предположим k=2 и один из векторов является:
v1 = {90,0,0,0,0}
в процессе решения оптимизационной задачи минимизации общего расстояния от центроидов-кандидатов предположим, что в какой-то момент, 2 центроиды-кандидаты:
c1 = {90,90,90,90,90}
c2 = {1000, 1000, 1000, 1000, 1000}
под управлением cosine_distance формула для (v1, c1) и (v1, c2) мы получаем точно такое же расстояние 0.5527864045 для обоих.
Я бы предположил, что v1 больше похож (ближе) на c1, чем c2. Очевидно, это не так.
Q1. Почему это предположение неверно?
Q2. Является ли косинусное расстояние правильной функцией расстояния для этого случая?
Q3. Что было бы лучше, учитывая природу проблема?
3 ответов
давайте разделим косинусное сходство на части и посмотрим как и почему это работает.
косинус угла между 2 векторами - a и b - определяется как:
cos(a, b) = sum(a .* b) / (length(a) * length(b))
здесь .* является умножением по элементам. Знаменатель здесь только для нормализации, поэтому давайте просто назовем его L. С ним наши функции превращаются в:
cos(a, b) = sum(a .* b) / L
, который, в свою очередь, может быть переписан как:
cos(a, b) = (a[1]*b[1] + a[2]*b[2] + ... + a[k]*b[k]) / L =
= a[1]*b[1]/L + a[2]*b[2]/L + ... + a[k]*b[k]/L
давайте немного абстрактнее и заменим x * y / L С функцией g(x, y) (L здесь константа, поэтому мы не ставим ее в качестве аргумента функции). Таким образом, наша косинусная функция становится:
cos(a, b) = g(a[1], b[1]) + g(a[2], b[2]) + ... + g(a[n], b[n])
то есть, каждая пара элементов (a[i], b[i]) is отдельно, и результат просто sum всех процедур. И это хорошо для вашего случая, потому что вы не хотите, чтобы разные пары (разные вершины) возились с каждым другое: если user1 посетил только vertex2 и user2 - только vertex1, то у них нет ничего общего, и сходство между ними должно быть нулевым. Что вам на самом деле не нравится, так это то, как сходство между отдельными парами - т. е. функция g() - рассчитывается.
С косинусной функцией сходство между отдельными парами выглядит так:
g(x, y) = x * y / L
здесь x и y представляют время, затраченное пользователями на вершину. И вот главный вопрос:--44-->тут умножение представляет сходство между отдельными парами хорошо? Я так не думаю. Пользователь, который провел 90 секунд на какой-то вершине, должен быть близок к пользователю, который провел там, скажем, 70 или 110 секунд, но гораздо дальше от пользователей, которые проводят там 1000 или 0 секунд. Умножение (даже нормализованное на L) здесь полностью вводит в заблуждение. Что значит умножить 2 периода времени?
хорошая новость заключается в том, что это вы, кто проектирует функцию подобия. Мы уже решили, что удовлетворены независимой обработкой пар (вершин), и нам нужна только индивидуальная функция подобия g(x, y) чтобы сделать что-то разумное с ее доводами. И что такое разумная функция для сравнения периодов времени? Я бы сказал, что вычитание-хороший кандидат:
g(x, y) = abs(x - y)
это не функция подобия, а функция расстояния-чем ближе значения друг к другу, тем меньше результат g() - но в конечном итоге идея одна и та же, поэтому мы можем обмениваться ими когда понадобится.
мы также можем захотеть увеличить влияние больших несоответствий путем возведения разницы в квадрат:
g(x, y) = (x - y)^2
Эй! Мы только что изобрели (среднее) квадратов ошибок! Теперь мы можем придерживаться MSE для расчета расстояния, или мы можем продолжить поиск хорошего
косинусное сходство предназначено для случая, когда вы делаете не хотите взять длину в accoun,но только угол. Если вы хотите также включить длину, выберите другую функцию расстояния.
Косинус расстояние is тесно связано с квадратным евклидовым расстоянием (единственное расстояние, для которого действительно определено k-среднее); поэтому сферическое k-среднее работает.
связь довольно проста:
квадрат евклидова расстояния sum_i (x_i-y_i)^2 можно учесть в sum_i x_i^2 + sum_i y_i^2 - 2 * sum_i x_i*y_i. Если оба вектора нормализованы, т. е. длина не имеет значения, то первые два условия 1. В этом случае, квадрат евклидова расстояния равен 2 - 2 * cos(x,y)!
другими словами: расстояние Косинуса в квадрате евклидово расстояние с данными, нормализованными к единичной длине.
Если вы не хотите нормализовать свои данные, не используйте Косинус.
Q1. Why is this assumption wrong?
как мы видим из определения, косинусное сходство измеряет угол между 2 векторами.
в вашем случае, вектор v1 лежит плашмя на первом измерении, в то время как c1 и c2 оба одинаково выровнены по осям, и, таким образом, косинусное сходство и чтобы быть таким же.
обратите внимание, что проблема заключается в c1 и c2 указывая в том же направлении. любой v1 будет иметь тот же Косинус сходство с ними обоими. Для примера :
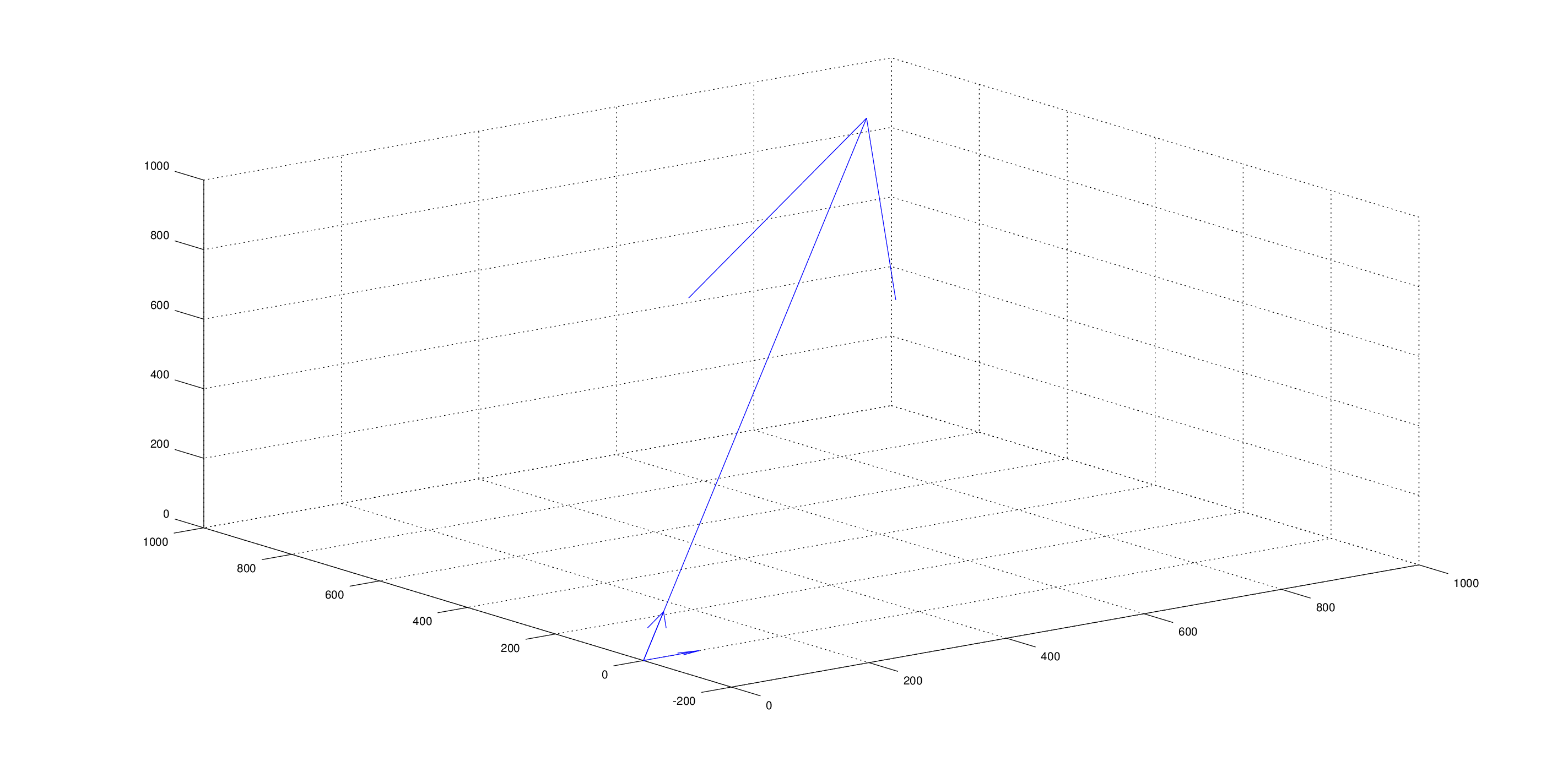
Q2. Is the cosine distance a correct distance function for this case?
как мы видим из примера в руке, наверное, нет.
Q3. What would be a better one given the nature of the problem?
считают Евклидово Расстояние.
