Косинусное сходство и tf-idf
меня смущает следующий комментарий TF-IDF и Косинус Сходство.
Я читал на обоих, а затем на wiki под Косинусным сходством я нахожу это предложение "в случае поиска информации косинусное сходство двух документов будет варьироваться от 0 до 1, так как термин частоты (TF-idf веса) не может быть отрицательным. Угол между двумя частотными векторами не может быть больше 90."
теперь я удивляющийся....разве это не две разные вещи?
tf-idf уже внутри косинусного подобия? Если да, то какого черта - я могу видеть только внутренние точечные произведения и евклидовы длины.
Я думал, что TF-idf-это то, что вы можете сделать до работает Косинус сходства на текстах. Я что-то пропустил?
5 ответов
TF-idf-это преобразование, которое вы применяете к текстам, чтобы получить два реальных вектора. Затем вы можете получить косинусное сходство любой пары векторов, взяв их точечное произведение и разделив его на произведение их норм. Что дает косинус угла между векторами.
Если d2 и q являются TF-idf векторами, то
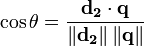
здесь θ - угол между векторами. Как θ колеблется от 0 до 90 градусов, cos θ колеблется от 1 до 0. θ можете только диапазон от 0 до 90 градусов, потому что векторы TF-idf неотрицательны.
нет особенно глубокой связи между tf-idf и моделью косинусного сходства / векторного пространства; TF-idf просто хорошо работает с матрицами документов. Однако он используется вне этой области, и в принципе вы можете заменить другое преобразование в ВСМ.
(Формула взята из Википедия, отсюда d2.)
TF-IDF-это просто способ измерить важность токенов в тексте; это просто очень распространенный способ превратить документ в список чисел (вектор термина, который обеспечивает один край угла, который вы получаете Косинус).
чтобы вычислить косинусное сходство, вам нужны два вектора документа; векторы представляют каждый уникальный термин с индексом, а значение этого индекса является некоторой мерой того, насколько важен этот термин для документа и для общей концепции документа сходство вообще.
вы можете просто подсчитать количество раз, когда каждый термин произошел в документе (Tэээ Frequency) и использовать этот целочисленный результат для оценки термина в векторе, но результаты будут не очень хорошими. Чрезвычайно распространенные термины (такие как" is"," and "и" the") могут привести к тому, что многие документы будут похожи друг на друга. (Эти примеры могут быть обработаны с помощью список стоп-слов, но и другие общие условия это недостаточно общее, чтобы считаться стоп-словом, вызывающим такую же проблему. В Stackoverflow слово "вопрос" может попасть в эту категорию. Если бы вы анализировали кулинарные рецепты, у вас, вероятно, возникли бы проблемы со словом "яйцо".)
TF-IDF корректирует частоту необработанного термина, принимая во внимание, как часто каждый термин происходит в целом (Document Frequency). Яnverse Document Frequency обычно является журналом количества документов, разделенных на количество документов, в которых встречается термин (изображение из Википедии):
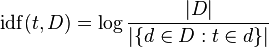
подумайте о "журнале" как о незначительном нюансе, который помогает вещам работать в долгосрочной перспективе-он растет, когда растет аргумент, поэтому, если термин редкий, IDF будет высоким (много документов, разделенных очень несколькими документами), если термин общий, IDF будет низким (много документов, разделенных множеством документов ~= 1).
скажем, у вас есть 100 рецептов, и все, кроме одного, требуют яйца, теперь у вас есть еще три документа, которые все содержат слово "яйцо", один раз в первом документе, два раза во втором документе и один раз в третьем документе. Частота термина "яйцо" в каждом документе равна 1 или 2, а частота документа-99 (или, возможно, 102, если считать новые документы. Давайте придерживаться 99).
TF-IDF "яйца" является:
1 * log (100/99) = 0.01 # document 1
2 * log (100/99) = 0.02 # document 2
1 * log (100/99) = 0.01 # document 3
Они все довольно маленькие цифры; напротив, давайте посмотрим на другое слово, которое встречается только в 9 из 100 рецептов корпуса: "руккола". Это происходит дважды в первом документе, три раза во втором и не происходит в третьем документе.
TF-IDF для "рукколы":
1 * log (100/9) = 2.40 # document 1
2 * log (100/9) = 4.81 # document 2
0 * log (100/9) = 0 # document 3
'руккола' - это действительно важно для документа 2, по крайней мере, по сравнению с "яйцом". Кого волнует, сколько раз произойдет яйцо? Все содержит яйцо! Эти векторы терминов намного более информативны, чем простые подсчеты, и они приведут к тому, что документы 1 и 2 будут намного ближе друг к другу (по отношению к документу 3), чем если бы использовались простые подсчеты терминов. В этом случае тот же результат, вероятно, возникнет (Эй! у нас здесь только два термина), но разница будет меньше.
take-home здесь заключается в том, что TF-IDF генерирует более полезные меры термина в документе, поэтому вы не фокусируетесь на действительно общих терминах (стоп-слова, "яйцо") и упускаете из виду важные термины ('руккола').
полная математическая процедура для косинусного сходства объясняется в этих учебниках
предположим, если вы хотите вычислить косинусное сходство между двумя документами, первым шагом будет вычисление векторов TF-idf двух документов. а потом найти скалярное произведение этих двух векторов. Эти учебники помогут вам:)
взвешивание tf/idf имеет некоторые случаи, когда они терпят неудачу и генерируют ошибку NaN в коде во время вычислений. Очень важно прочитать это: http://www.p-value.info/2013/02/when-tfidf-and-cosine-similarity-fail.html
TF-idf просто используется для поиска векторов из документов на основе частоты TF - Term, которая используется для определения того, сколько раз термин встречается в документе и обратной частоте документа, что дает меру того, сколько раз термин появляется во всей коллекции.
затем вы можете найти Косинус сходство между документами.
