Лево-Линейная и право-Линейная грамматики

построение эквивалентной регулярной грамматики из регулярного выражения

во-первых, я начинаю с некоторых простых правил для построения регулярной грамматики(RG) из регулярного выражения(RE).
Я пишу правила для правой линейной грамматики (оставляя в качестве упражнения писать аналогичные правила для левой линейной грамматики)

Примечание: заглавные буквы используются для переменных и небольшие для терминалов в грамматике. Нулевой символ -^. Термин 'любой номер' означает ноль или более раз, * закрытие звездой.

[ОСНОВНАЯ ИДЕЯ]

• ОДИНОЧНЫЙ ТЕРМИНАЛ: если RE просто e (e being any terminal), мы можем написать G, только с одним правилом производства S --> e (где S is the start symbol), является эквивалентным RG.

• ОПЕРАЦИЯ ОБЪЕДИНЕНИЯ: если RE имеет форму e + f, где e and f are terminals, мы можем написать G, С два производственных правила S --> e | f, является эквивалентным RG.

• конкатенация: если RE имеет форму ef, где e and f are terminals, мы можем написать G, С двумя правилами производства S --> eA, A --> f, является эквивалентным RG.

• ЗАКРЫТИЕ ЗВЕЗДЫ: если RE имеет форму e*, где e is a terminal и * Kleene star closure операция, мы можем написать два производственных правила в G, S --> eS | ^, это эквивалент RG.

• ПЛЮС ЗАКРЫТИЕ: если RE имеет форму e⁺, где e is a terminal и + Kleene plus closure операция, мы можем написать два производственных правила в G, S --> eS | e, является эквивалентным RG.

• ЗАКРЫТИЕ ЗВЕЗДЫ НА СОЮЗЕ: если RE имеет вид (e + f)*, где оба e and f are terminals, мы можем написать три правила производства G, S --> eS | fS | ^, является эквивалентным RG.

• ПЛЮС ЗАКРЫТИЕ НА UNION: если RE имеет вид (e + f)⁺, где e and f are terminals, мы можем написать четыре правила производства G, S --> eS | fS | e | f, является эквивалентным RG.

• ЗАКРЫТИЕ ЗВЕЗДЫ НА КОНКАТЕНАЦИИ: если RE имеет форму (ef)*, где оба e and f are terminals, мы можем написать три правила производства G, S --> eA | ^, A --> fS, является эквивалентным RG.

• ПЛЮС ЗАКРЫТИЕ КОНКАТЕНАЦИИ: если RE имеет форму (ef)⁺, где e and f are terminals, мы можем написать три правила производства G, S --> eA, A --> fS | f, является эквивалентным RG.

убедитесь, что вы понимаете все вышеперечисленные правила, вот сводная таблица:

+-------------------------------+--------------------+------------------------+
| TYPE                          | REGULAR-EXPRESSION | RIGHT-LINEAR-GRAMMAR   |
+-------------------------------+--------------------+------------------------+
| SINGLE TERMINAL               | e                  | S --> e                |
| UNION OPERATION               | e + f              | S --> e | f            |
| CONCATENATION                 | ef                 | S --> eA, A --> f      |
| STAR CLOSURE                  | e*                 | S --> eS | ^           |
| PLUS CLOSURE                  | e+                 | S --> eS | e           |
| STAR CLOSURE ON UNION         | (e + f)*           | S --> eS | fS | ^      |
| PLUS CLOSURE ON UNION         | (e + f)+           | S --> eS | fS | e | f  |
| STAR CLOSURE ON CONCATENATION | (ef)*              | S --> eA | ^, A --> fS |
| PLUS CLOSURE ON CONCATENATION | (ef)+              | S --> eA, A --> fS | f |
+-------------------------------+--------------------+------------------------+

Примечание: символ e и f являются терминалами, ^ является нулевым символом и S начало переменной

[ответ]

a) (0+1)*00(0+1)*

язык описание: все строки состоят из 0s и 1s, содержащие по крайней мере одну пару 00.

• Правая Линейная Грамматика:

  S --> 0S | 1S / 00A
  A --> 0A | 1A / ^

  строка может начинаться с любой строкой 0s и 1s Вот почему включены правила s --> 0S | 1S и потому, что по-крайней мере одна пара 00 ,нет нулевого символа. S --> 00A включается, поскольку 0, 1 может быть после 00. Символ A заботится о 0 и 1 после 00.

• Левая Линейная Грамматика:

  S --> S0 | S1 / A00
  A --> A0 | A1 / ^

б) 0*(1(0+1))*

язык описание: любое число 0, затем любое число 10 и 11.
{ потому что 1(0 + 1) = 10 + 11 }

• Правая Линейная Грамматика:

  S --> 0S | A/^
  A --> 1B
  B -- > 0A | 1A | 0 / 1

  строка начинается с любого числа 0 так что правило S --> 0S | ^ несколько Включено, затем правило для генерации 10 и 11 для любого количества раз, используя A --> 1B and B --> 0A | 1A | 0 | 1.

  другая альтернативная правая линейная грамматика может быть

  S --> 0S | A/^
  A -- > 10A | 11A | 10 / 11

• Левая Линейная Грамматика:

  S --> A/^
  A --> A10 | A11 / B
  B --> B0 / 0

  альтернативной формой может быть

  S --> S10 | S11 | B/^
  Си>-- B0 / 0

c) (((01+10)*11)*00)*

язык описание: во-первых, язык содержит строку null (^), потому что есть * (звезда) снаружи каждой вещи, присутствующей внутри (). Также, если строка в языке не равна null, которая вызывающе заканчивается на 00. Можно просто представить себе это регулярное выражение в виде (((A)* B) * C)*, где (A)* - (01 + 10)*, то есть любое число повторов 01 и 10. Если есть является ли экземпляр a в строке, будет B вызывающе, потому что (A)*B и B равно 11.
Некоторые примеры строк { ^, 00, 0000, 000000, 1100, 111100, 1100111100, 011100, 101100, 01110000, 01101100, 0101011010101100, 101001110001101100 ....}

• Левая Линейная Грамматика:

  S --> A00/^
  A --> B11 / S
  B --> B01 | B10 / A

  S --> A00 | ^ потому что любая строка либо null, либо если это не null он заканчивается на 00. Когда строка заканчивается на 00 переменная A соответствует шаблону ((01 + 10)* + 11)*. Опять же, этот шаблон может быть нулевым или должен заканчиваться на 11. Если его null, то A совпадает с S опять я.e строка заканчивается шаблоном like (00)*. Если шаблон не равен null,B совпадает с (01 + 10)*. Когда B матчи все возможное, A снова начинает соответствовать строке. Это закрывает out-most * in ((01 + 10)* + 11)*.

• Правая Линейная Грамматика:

  S --> A / 00S/^
  A -- > 01A | 10A / 11S

вторая часть вопроса:

For a) I have the following:
Left-linear
S --> B00 | S11
B --> B0|B1|011

Right-linear
S --> 00B | 11S
B --> 0B|1B|0|1

(ответ)
Вы решение неправильно по следующим причинам,

левая линейная грамматика неверна, потому что string 0010 невозможно создать. Правильно-линейная грамматика неверна Потому что string 1000 невозможно создать. Хотя оба они на языке, генерируемом регулярным выражением вопроса (a).

редактировать
Добавление DFA для каждого регулярного выражения. чтобы можно было найти его полезным.

a) (0+1)*00(0+1)*

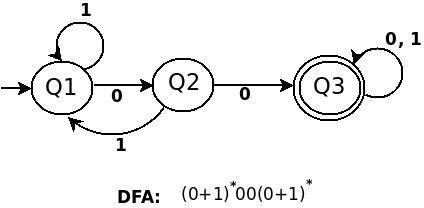
б) 0*(1(0+1))*

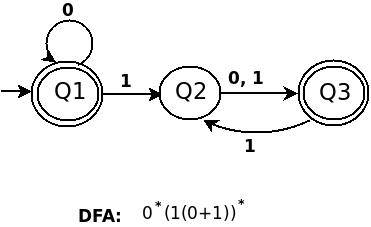
c) (((01+10)*11)*00)*

рисование DFA для этого регулярного выражения является трюком и сложным.
_{для этого я хотел добавить DFA в}

чтобы упростить задачу, мы должны думать, что вид формирования RE мне огонь (((01+10)*11)*00)* выглядит так:(a*b)*

(((01+10)*11)* 00 )*
(          a*   b )*

собственно в приведенном выше выражении a в форме (a*b)* это ((01+10)*11)*

RE (a*b)* равна (a + b)*b + ^. DFA для (Ab) в belows:

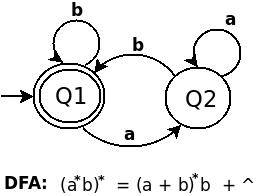
DFA для ((01+10)*11)* - это:

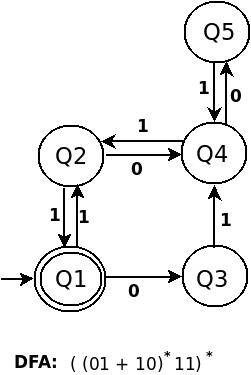
DFA для (((01+10)*11)* 00 )* - это:

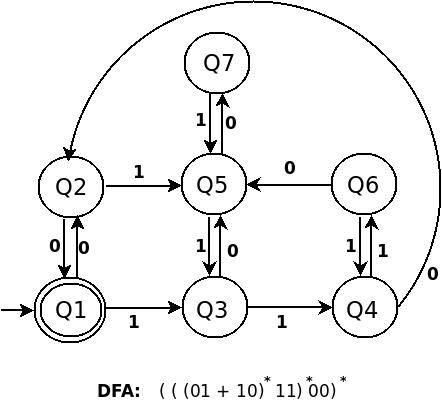
_{попробуйте найти сходство в строительстве выше трех DFA. не двигайтесь вперед, пока не поймете первого!--316-->}