Лучшие результаты в разделе set, чем при различиях

существует много работ, описывающих различные расширенные алгоритмы разбиения множеств. Вот только два из них:--3-->

• "полный алгоритм в любое время для разбиения чисел" Ричард Э. Корф.
• "эффективная полностью полиномиальная аппроксимационная схема для задачи подмножества-суммы" Ханс Келлерер и др.

честно говоря, я не знаю, какой из них дает более эффективное решение. Наверное, ни один из этих передовые алгоритмы, необходимые для решения этой проблемы SPOJ. Статья Корфа все еще очень полезна. Алгоритмы, описанные там, очень просты (для понимания и реализации). Также он рассматривает несколько еще более простых алгоритмов (в разделе 2). Поэтому, если вы хотите узнать подробности методов Горовица-Сахни или Шреппеля-Шамира (упомянутых ниже), вы можете найти их в статье Корфа. Также (в разделе 8) он пишет, что стохастические подходы не гарантируют достаточно хороших решений. Так что вряд ли вы получите значительные улучшения с чем-то вроде восхождения на холм, имитационного отжига или поиска табу.

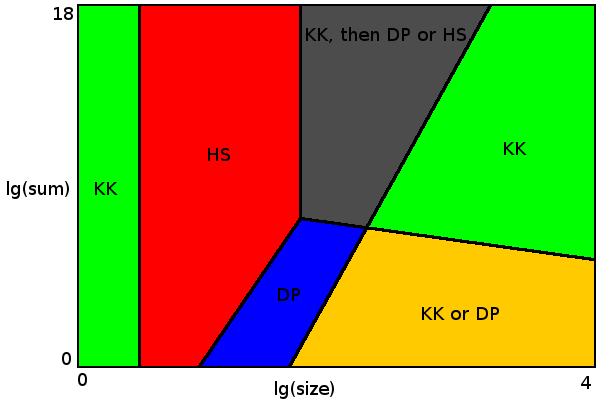
я попробовал несколько простых алгоритмов и их комбинаций для решения проблем разбиения с размером до 10000, максимальное значение до 10¹⁴, и ограничение по времени 4 сек. Они были проверены на случайных равномерно распределенных числах. И оптимальное решение было найдено для каждого экземпляра проблемы, который я пробовал. Для некоторых экземпляров задачи оптимальность гарантируется алгоритмом, для других оптимальность не гарантируется на 100%, но вероятность получения неоптимального решения очень мала.

для размеров до 4 (зеленая область слева) алгоритм Кармаркара-карпа всегда дает оптимальный результат.

для размеров до 54 алгоритм грубой силы достаточно быстр (красная область). Существует выбор между алгоритмами Горовица-Сахни или Шреппеля-Шамира. Я использовал Horowitz-Sahni, потому что он кажется более эффективным для заданных пределов. Schroeppel-Shamir использует гораздо меньше памяти (все помещается в кеш L2), поэтому может быть предпочтительнее, когда другие ядра ЦП выполняют некоторые задачи с интенсивной памятью или делают разделение с использованием нескольких потоков. Или решить большие проблемы с не столь строгим ограничением по времени (где у Горовица-Сахни просто заканчивается память).

когда размер, умноженный на сумму всех значений, меньше 5 * 10⁹ (синяя область), подход динамического программирования применим. Граница между грубой силой и области динамического программирования на диаграмме показывают, где каждый алгоритм работает лучше.

зеленая зона справа-это место, где алгоритм Кармаркара-карпа дает оптимальный результат с почти 100% вероятностью. Здесь так много совершенных вариантов разбиения (с дельтой 0 или 1), что алгоритм Кармаркара-карпа почти наверняка найдет один из них. Можно изобрести набор данных, где Кармаркар-Карп всегда дает неоптимальный результат. Например {17 13 10 10 10 ...}. Если вы умножите это для некоторого большого числа ни KK, ни DP не смогут найти оптимальное решение. К счастью, на практике такие наборы данных весьма маловероятны. Но проблемный сеттер может добавить такой набор данных, чтобы сделать конкурс более сложным. В этом случае вы можете выбрать расширенный алгоритм для улучшения результатов (но только для серых и правых зеленых областей на диаграмме).

я попробовал 2 способа реализации очереди приоритетов алгоритма Кармаркара-карпа: с максимальной кучей и с отсортированным массивом. Опция отсортированного массива немного быстрее с линейным поиском и значительно быстрее с бинарным поиском.

желтая область-это место, где вы можете выбрать между гарантированным оптимальным результатом (с DP) или просто оптимальным результатом с высокой вероятностью (с Karmarkar-Karp).

наконец, серая область, где ни один из простых алгоритмов сам по себе не дает оптимального результата. Здесь мы могли бы использовать Karmarkar-Karp для предварительной обработки данных, пока она не будет применима к Горовиц-Сахни или динамическому программированию. В этом месте есть также много совершенных вариантов разделения, но меньше, чем в зеленой зоне, поэтому Karmarkar-Karp сам по себе может иногда пропустить правильное разделение. Update: как отметил @mhum, нет необходимости реализовывать алгоритм динамического программирования, чтобы заставить вещи работать. Горовиц-Сахни с предварительной обработкой Кармаркар-карпа достаточно. Но важно, чтобы алгоритм Горовица-Сахни работал на размерах до 54 в указанный срок, чтобы (почти) гарантировать оптимальное разбиение. Так C++ или другой язык с хорошим предпочтительнее оптимизировать компилятор и быстрый компьютер.

вот как я объединил Кармаркар-Карп с другими алгоритмами:

template<bool Preprocess = false>
i64 kk(const vector<i64>& values, i64 sum, Log& log)
{
    log.name("Karmarkar-Karp");
    vector<i64> pq(values.size() * 2);
    copy(begin(values), end(values), begin(pq) + values.size());
    sort(begin(pq) + values.size(), end(pq));
    auto first = end(pq);
    auto last = begin(pq) + values.size();

    while (first - last > 1)
    {
        if (Preprocess && first - last <= kHSLimit)
        {
            hs(last, first, sum, log);
            return 0;
        }
        if (Preprocess && static_cast<double>(first - last) * sum <= kDPLimit)
        {
            dp(last, first, sum, log);
            return 0;
        }
        const auto diff = *(first - 1) - *(first - 2);
        sum -= *(first - 2) * 2;
        first -= 2;
        const auto place = lower_bound(last, first, diff);
        --last;
        copy(last + 1, place, last);
        *(place - 1) = diff;
    }

    const auto result = (first - last)? *last: 0;
    log(result);
    return result;
}

ссылка на полную реализацию C++11. эта программа определяет только разницу между суммами разделов, она не сообщает о самих разделах. предупреждение: если вы хотите запустить его на компьютере со свободной памятью менее 1 Гб, уменьшите kHSLimit константы.

редактировать вот реализация, которая начинается с дифференцирования Karmarkar-Karp, а затем пытается оптимизировать результирующие разделы.

единственными оптимизациями, которые позволяет время, являются даю 1 из одного раздела в другой и замена 1 на 1 между обоими разделами.

моя реализация Кармаркар-карпа в начале должна быть неточной, так как результирующий счет только с Кармаркар-карпом 2.711483 не 11.796614 пунктов, цитируемых OP. Счет идет на 7.718049 при использовании оптимизации.

спойлер предупреждение C# код отправки следует

using System;
using System.Collections.Generic;
using System.Linq;
public class Test
{
    // some comparer's to lazily avoid using a proper max-heap implementation
    public class Index0 : IComparer<long[]>
    {
        public int Compare(long[] x, long[] y)
        {
            if(x[0] == y[0]) return 0;
            return x[0] < y[0] ? -1 : 1;
        }
        public static Index0 Inst = new Index0();
    }
    public class Index1 : IComparer<long[]>
    {
        public int Compare(long[] x, long[] y)
        {
            if(x[1] == y[1]) return 0;
            return x[1] < y[1] ? -1 : 1;
        }
    }

    public static void Main()
    {
        // load the data
        var start = DateTime.Now;
        var list = new List<long[]>();
        int size = int.Parse(Console.ReadLine());
        for(int i=1; i<=size; i++) {
            var tuple = new long[]{ long.Parse(Console.ReadLine()), i };
            list.Add(tuple);
        }
        list.Sort((x, y) => { if(x[0] == y[0]) return 0; return x[0] < y[0] ? -1 : 1; });

        // Karmarkar-Karp differences
        List<long[]> diffs = new List<long[]>();
        while(list.Count > 1) {
            // get max
            var b = list[list.Count - 1];
            list.RemoveAt(list.Count - 1);
            // get max
            var a = list[list.Count - 1];
            list.RemoveAt(list.Count - 1);
            // (b - a)
            var diff = b[0] - a[0];
            var tuple = new long[]{ diff, -1 };
            diffs.Add(new long[] { a[0], b[0], diff, a[1], b[1] });
            // insert (b - a) back in
            var fnd = list.BinarySearch(tuple, new Index0());
            list.Insert(fnd < 0 ? ~fnd : fnd, tuple);
        }
        var approx = list[0];
        list.Clear();

        // setup paritions
        var listA = new List<long[]>();
        var listB = new List<long[]>();
        long sumA = 0;
        long sumB = 0;

        // Karmarkar-Karp rebuild partitions from differences
        bool toggle = false;
        for(int i=diffs.Count-1; i>=0; i--) {
            var inB = listB.BinarySearch(new long[]{diffs[i][2]}, Index0.Inst);
            var inA = listA.BinarySearch(new long[]{diffs[i][2]}, Index0.Inst);
            if(inB >= 0 && inA >= 0) {
                toggle = !toggle;
            }
            if(toggle == false) {
                if(inB >= 0) {
                    listB.RemoveAt(inB);
                }else if(inA >= 0) {
                    listA.RemoveAt(inA);
                }
                var tb = new long[]{diffs[i][1], diffs[i][4]};
                var ta = new long[]{diffs[i][0], diffs[i][3]};
                var fb = listB.BinarySearch(tb, Index0.Inst);
                var fa = listA.BinarySearch(ta, Index0.Inst);
                listB.Insert(fb < 0 ? ~fb : fb, tb);
                listA.Insert(fa < 0 ? ~fa : fa, ta);
            } else {
                if(inA >= 0) {
                    listA.RemoveAt(inA);
                }else if(inB >= 0) {
                    listB.RemoveAt(inB);
                }
                var tb = new long[]{diffs[i][1], diffs[i][4]};
                var ta = new long[]{diffs[i][0], diffs[i][3]};
                var fb = listA.BinarySearch(tb, Index0.Inst);
                var fa = listB.BinarySearch(ta, Index0.Inst);
                listA.Insert(fb < 0 ? ~fb : fb, tb);
                listB.Insert(fa < 0 ? ~fa : fa, ta);
            }
        }
        listA.ForEach(a => sumA += a[0]);
        listB.ForEach(b => sumB += b[0]);

        // optimize our partitions with give/take 1 or swap 1 for 1
        bool change = false;
        while(DateTime.Now.Subtract(start).TotalSeconds < 4.8) {
            change = false;
            // give one from A to B
            for(int i=0; i<listA.Count; i++) {
                var a = listA[i];
                if(Math.Abs(sumA - sumB) > Math.Abs((sumA - a[0]) - (sumB + a[0]))) {
                    var fb = listB.BinarySearch(a, Index0.Inst);
                    listB.Insert(fb < 0 ? ~fb : fb, a);
                    listA.RemoveAt(i);
                    i--;
                    sumA -= a[0];
                    sumB += a[0];
                    change = true;
                } else {break;}
            }
            // give one from B to A
            for(int i=0; i<listB.Count; i++) {
                var b = listB[i];
                if(Math.Abs(sumA - sumB) > Math.Abs((sumA + b[0]) - (sumB - b[0]))) {
                    var fa = listA.BinarySearch(b, Index0.Inst);
                    listA.Insert(fa < 0 ? ~fa : fa, b);
                    listB.RemoveAt(i);
                    i--;
                    sumA += b[0];
                    sumB -= b[0];
                    change = true;
                } else {break;}
            }
            // swap 1 for 1
            for(int i=0; i<listA.Count; i++) {
                var a = listA[i];
                for(int j=0; j<listB.Count; j++) {
                    var b = listB[j];
                    if(Math.Abs(sumA - sumB) > Math.Abs((sumA - a[0] + b[0]) - (sumB -b[0] + a[0]))) {
                        listA.RemoveAt(i);
                        listB.RemoveAt(j);
                        var fa = listA.BinarySearch(b, Index0.Inst);
                        var fb = listB.BinarySearch(a, Index0.Inst);
                        listA.Insert(fa < 0 ? ~fa : fa, b);
                        listB.Insert(fb < 0 ? ~fb : fb, a);
                        sumA = sumA - a[0] + b[0];
                        sumB = sumB - b[0] + a[0];
                        change = true;
                        break;
                    }
                }
            }
            //
            if(change == false) { break; }
        }

        /*
        // further optimization with 2 for 1 swaps
        while(DateTime.Now.Subtract(start).TotalSeconds < 4.8) {
            change = false;
            // trade 2 for 1
            for(int i=0; i<listA.Count >> 1; i++) {
                var a1 = listA[i];
                var a2 = listA[listA.Count - 1 - i];
                for(int j=0; j<listB.Count; j++) {
                    var b = listB[j];
                    if(Math.Abs(sumA - sumB) > Math.Abs((sumA - a1[0] - a2[0] + b[0]) - (sumB - b[0] + a1[0] + a2[0]))) {
                        listA.RemoveAt(listA.Count - 1 - i);
                        listA.RemoveAt(i);
                        listB.RemoveAt(j);
                        var fa = listA.BinarySearch(b, Index0.Inst);
                        var fb1 = listB.BinarySearch(a1, Index0.Inst);
                        var fb2 = listB.BinarySearch(a2, Index0.Inst);
                        listA.Insert(fa < 0 ? ~fa : fa, b);
                        listB.Insert(fb1 < 0 ? ~fb1 : fb1, a1);
                        listB.Insert(fb2 < 0 ? ~fb2 : fb2, a2);
                        sumA = sumA - a1[0] - a2[0] + b[0];
                        sumB = sumB - b[0] + a1[0] + a2[0];
                        change = true;
                        break;
                    }
                }
            }
            //
            if(DateTime.Now.Subtract(start).TotalSeconds > 4.8) { break; }
            // trade 2 for 1
            for(int i=0; i<listB.Count >> 1; i++) {
                var b1 = listB[i];
                var b2 = listB[listB.Count - 1 - i];
                for(int j=0; j<listA.Count; j++) {
                    var a = listA[j];
                    if(Math.Abs(sumA - sumB) > Math.Abs((sumA - a[0] + b1[0] + b2[0]) - (sumB - b1[0] - b2[0] + a[0]))) {
                        listB.RemoveAt(listB.Count - 1 - i);
                        listB.RemoveAt(i);
                        listA.RemoveAt(j);
                        var fa1 = listA.BinarySearch(b1, Index0.Inst);
                        var fa2 = listA.BinarySearch(b2, Index0.Inst);
                        var fb = listB.BinarySearch(a, Index0.Inst);
                        listA.Insert(fa1 < 0 ? ~fa1 : fa1, b1);
                        listA.Insert(fa2 < 0 ? ~fa2 : fa2, b2);
                        listB.Insert(fb < 0 ? ~fb : fb, a);
                        sumA = sumA - a[0] + b1[0] + b2[0];
                        sumB = sumB - b1[0] - b2[0] + a[0];
                        change = true;
                        break;
                    }
                }
            }
            //
            if(change == false) { break; }
        }
        */

        // output the correct ordered values
        listA.Sort(new Index1());
        foreach(var t in listA) {
            Console.WriteLine(t[1]);
        }

        // DEBUG/TESTING
        //Console.WriteLine(approx[0]);
        //foreach(var t in listA) Console.Write(": " + t[0] + "," + t[1]);
        //Console.WriteLine();
        //foreach(var t in listB) Console.Write(": " + t[0] + "," + t[1]);

    }
}