Максимальная активная просадка в python
недавно я задал вопрос о расчет максимальной просадки здесь Александр дал очень краткий и эффективный способ вычисления его с помощью методов фрейма данных в панд.
Я хотел продолжить, спросив, как другие вычисляют максимум активный просадка?
это вычисляет максимальную просадку. Нет! Максимальная Активная Просадка
Это то, что я реализовал для максимальной просадки на основе Ответ Александра на вопрос, связанный выше:
def max_drawdown_absolute(returns):
r = returns.add(1).cumprod()
dd = r.div(r.cummax()).sub(1)
mdd = dd.min()
end = dd.argmin()
start = r.loc[:end].argmax()
return mdd, start, end
он принимает серию возврата и возвращает max_drawdown вместе с индексами, для которых произошла просадка.
мы начинаем с генерации серии кумулятивных возвратов, чтобы действовать как индекс возврата.
r = returns.add(1).cumprod()
в каждый момент времени текущая просадка рассчитывается путем сравнения текущего уровня индекса возврата с максимальным индексом возврата для всех периодов прежде.
dd = r.div(r.cummax()).sub(1)
максимальная просадка - это минимум всех рассчитанных просадок.
мой вопрос:
Я хотел продолжить, спросив, как другие вычисляют максимум активный просадка?
предполагает, что решение будет распространяться на решение выше.
3 ответов
начиная с серии возвратов портфеля и контрольных возвратов, мы строим кумулятивные доходы для обоих. предполагается, что переменные ниже уже находятся в кумулятивном пространстве возврата.
активный возврат из периода j на срок я - это:
решение
вот как мы можем расширить Абсолют решение:
def max_draw_down_relative(p, b):
p = p.add(1).cumprod()
b = b.add(1).cumprod()
pmb = p - b
cam = pmb.expanding(min_periods=1).apply(lambda x: x.argmax())
p0 = pd.Series(p.iloc[cam.values.astype(int)].values, index=p.index)
b0 = pd.Series(b.iloc[cam.values.astype(int)].values, index=b.index)
dd = (p * b0 - b * p0) / (p0 * b0)
mdd = dd.min()
end = dd.argmin()
start = cam.ix[end]
return mdd, start, end
объяснение
подобно абсолютному случаю, в каждый момент времени мы хотим знать, какой максимальный кумулятивный активный доход был до этого момента. Мы получаем эту серию кумулятивных активных возвратов с p - b. Разница в том, что мы хотим отслеживать, какими были p и b в это время, а не саму разницу.
Итак, мы генерируем серию'когда', захваченных в cam (cumulative argmax) и последующие серии значений портфеля и бенчмарка на тех"когда'.
p0 = pd.Series(p.ix[cam.values.astype(int)].values, index=p.index)
b0 = pd.Series(b.ix[cam.values.astype(int)].values, index=b.index)
caclulation просадки теперь можно сделать аналогично используя формулу выше:
dd = (p * b0 - b * p0) / (p0 * b0)
демонстрация
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
np.random.seed(314)
p = pd.Series(np.random.randn(200) / 100 + 0.001)
b = pd.Series(np.random.randn(200) / 100 + 0.001)
keys = ['Portfolio', 'Benchmark']
cum = pd.concat([p, b], axis=1, keys=keys).add(1).cumprod()
cum['Active'] = cum.Portfolio - cum.Benchmark
mdd, sd, ed = max_draw_down_relative(p, b)
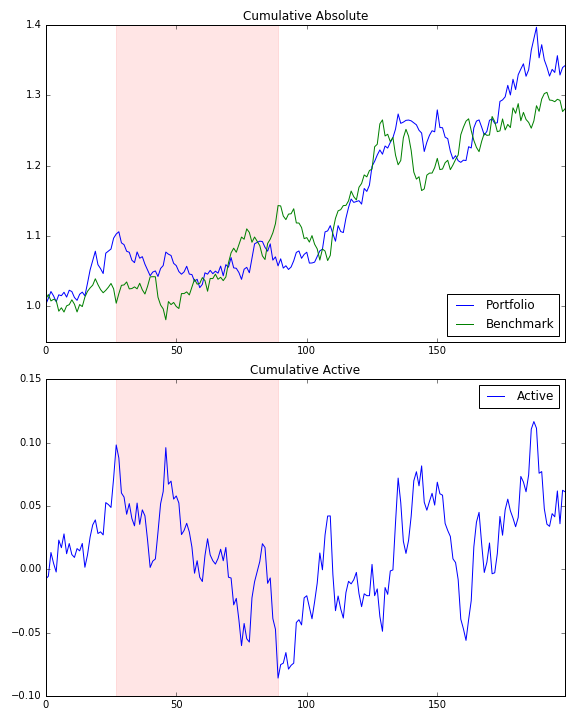
f, a = plt.subplots(2, 1, figsize=[8, 10])
cum[['Portfolio', 'Benchmark']].plot(title='Cumulative Absolute', ax=a[0])
a[0].axvspan(sd, ed, alpha=0.1, color='r')
cum[['Active']].plot(title='Cumulative Active', ax=a[1])
a[1].axvspan(sd, ed, alpha=0.1, color='r')
возможно, вы заметили, что ваши отдельные компоненты не равны целому, ни аддитивным, ни геометрическим образом:
>>> cum.tail(1)
Portfolio Benchmark Active
199 1.342179 1.280958 1.025144
это всегда тревожная ситуация, так как это указывает на то, что в вашей модели может произойти какая-то утечка.
смешивание одного периода и многопериодной атрибуции всегда является проблемой. Часть проблемы заключается в цели анализа, то есть в том, что вы пытаетесь объяснить.
если вы смотрите на кумулятивные возвраты как и в случае выше, то один из способов выполнения анализа заключается в следующем:
убедитесь, что доходность портфеля и контрольная доходность являются избыточной доходностью, т. е. вычитают соответствующую денежную доходность за соответствующий период (например, ежедневно, ежемесячно и т. д.).
Предположим, у вас есть богатый дядя, который одалживает вам $ 100m, чтобы начать свой фонд. Теперь вы можете думать о своем портфеле как о трех транзакциях, одной денежной и двух производных операции: a) инвестируйте свои $100m в денежный счет, удобно зарабатывая ставку предложения. b) ввести в капитал своп на $ 100м условный c) заключите сделку свопа с нулевым бета-хедж-фондом, опять же за $100m условно.
мы удобно предположим, что обе своп-транзакции обеспечиваются денежным счетом и что нет никаких транзакционных издержек (если только...!).
в первый день фондовый индекс вырос чуть более чем на 1% (an сверхприбыль ровно 1,00% после вычета кассового расхода за день). Некоррелированный хедж-фонд, однако, предоставил избыточную доходность -5%. Наш фонд сейчас составляет $ 96m.
день второй, как мы перебалансируем? Ваши расчеты подразумевают, что мы никогда этого не делаем. Каждый представляет собой отдельный портфель, который дрейфует вечно... Однако для целей атрибуции я считаю, что имеет смысл ежедневно перебалансировать, то есть 100% для каждой из двух стратегий.
как это просто условные экспозиции с достаточным денежным обеспечением, мы можем просто скорректировать суммы. Таким образом, вместо того, чтобы иметь $101m воздействия индекса акций на второй день и $95m воздействия хедж-фонда, мы вместо этого перебалансировка (при нулевой стоимости), так что у нас есть $96m воздействия каждого.
как это работает в панд, спросите вы? Вы уже рассчитали cum['Portfolio'], который является совокупным избыточным фактором роста портфеля (т. е. после вычета денежной прибыли). Если мы применяем текущий день превышение ориентира и возвращается в активный фактор роста портфеля в предыдущий день, мы вычисляем ежедневные ребаланс возвращает.
import numpy as np
import pandas as pd
np.random.seed(314)
df_returns = pd.DataFrame({
'Portfolio': np.random.randn(200) / 100 + 0.001,
'Benchmark': np.random.randn(200) / 100 + 0.001})
df_returns['Active'] = df.Portfolio - df.Benchmark
# Copy return dataframe shape and fill with NaNs.
df_cum = pd.DataFrame()
# Calculate cumulative portfolio growth
df_cum['Portfolio'] = (1 + df_returns.Portfolio).cumprod()
# Calculate shifted portfolio growth factors.
portfolio_return_factors = pd.Series([1] + df_cum['Portfolio'].shift()[1:].tolist(), name='Portfolio_return_factor')
# Use portfolio return factors to calculate daily rebalanced returns.
df_cum['Benchmark'] = (df_returns.Benchmark * portfolio_return_factors).cumsum()
df_cum['Active'] = (df_returns.Active * portfolio_return_factors).cumsum()
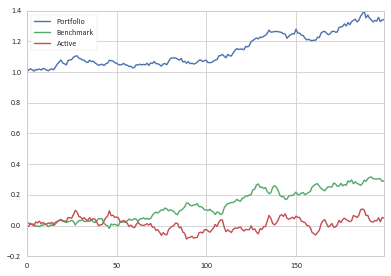
теперь мы видим, что активная доходность плюс базовая доходность плюс начальные денежные средства равны текущей стоимости портфеля.
>>> df_cum.tail(3)[['Benchmark', 'Active', 'Portfolio']]
Benchmark Active Portfolio
197 0.303995 0.024725 1.328720
198 0.287709 0.051606 1.339315
199 0.292082 0.050098 1.342179
при строительстве df_cum['Portfolio'] = 1 + df_cum['Benchmark'] + df_cum['Active'].
Потому что этот метод трудно вычислить (без панд!) и понять (большинство людей не получат условный exposures), отраслевая практика обычно определяет активную доходность как совокупную разницу в доходности за определенный период времени. Например, если фонд вырос на 5,0% в месяц, а рынок упал на 1,0%, то избыточная доходность за этот месяц обычно определяется как +6,0%. Проблема с этим упрощенным подходом, однако, заключается в том, что ваши результаты будут дрейфовать друг от друга с течением времени из-за усложнения и перебалансировки проблем, которые должным образом не учитываются в расчетах.
так дали наши!--6--> столбец, мы могли бы определить просадку как:
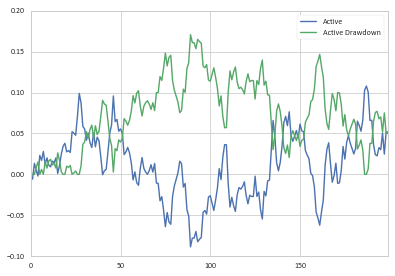
drawdown = pd.Series(1 - (1 + df_cum.Active)/(1 + df_cum.Active.cummax()), name='Active Drawdown')
>>> df_cum.Active.plot(legend=True);drawdown.plot(legend=True)
затем вы можете определить начальную и конечную точки просадки, как вы это делали ранее.
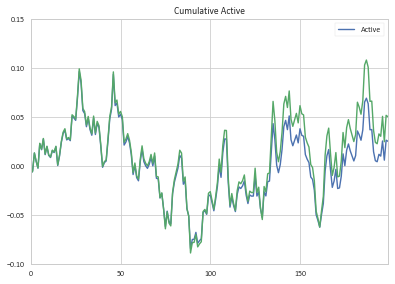
сравнивая мой кумулятивный активный вклад возврата с суммами, которые вы рассчитали, вы обнаружите, что они сначала похожи, а затем дрейфуют друг от друга с течением времени (мои расчеты возврата в зеленом цвете):
мои дешевые два Пенни в чистом Python:
def find_drawdown(lista):
peak = 0
trough = 0
drawdown = 0
for n in lista:
if n > peak:
peak = n
trough = peak
if n < trough:
trough = n
temp_dd = peak - trough
if temp_dd > drawdown:
drawdown = temp_dd
return -drawdown