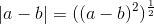Математически найти максимальное значение без условного сравнения

Я думаю, это было бы самым простым, если бы нам удалось найти разницу между двумя числами (только величина не знак)

max = ((a+b)+|a-b|)/2;

здесь |a-b| является величиной разницы между a и b.

Если вы не можете доверять своей среде для создания соответствующих операций без ветвей, когда они доступны, см. на этой странице для дальнейших действий. Обратите внимание на ограничение диапазона ввода; используйте для операции более крупный целочисленный тип, если вы не можете гарантировать, что ваши входные данные будут соответствовать.

решения без условия. Приведите к uint, затем вернитесь к int, чтобы получить abs.

int abs (a) { return (int)((unsigned int)a); }
int max (a, b) { return (a + b + abs(a - b)) / 2; }

int max3 (a, b, c) { return (max(max(a,b),c); }

используя только логические операции, оценку короткого замыкания и предполагая соглашение c округления до нуля, можно выразить это как:

int lt0(int x) {
    return x && (!!((x-1)/x));
}

int mymax(int a, int b) {
    return lt0(a-b)*b+lt0(b-a)*a;
}

основная идея заключается в реализации оператора сравнения, который будет возвращать 0 или 1. Можно сделать аналогичный трюк, если ваш язык сценариев следует соглашению округления к значению пола, как это делает python.

Хммм. Я предполагаю, что нет, и, и или побитовые? Если это так, для решения этой проблемы будет побитовое выражение. Обратите внимание, что A | B даст число >= A и >= B. возможно, есть метод обрезки для выбора числа с наибольшим количеством битов.

чтобы расширить, нам нужно следующее, Чтобы определить, является ли a (0) или B (1) больше.

таблица истинности:

0|0 = 0  
0|1 = 1
1|0 = 0
1|1 = 0

!A and B

поэтому, даст индекс большего бита. Ergo, сравните каждый бит в обоих числах, и если они разные, используйте приведенное выше выражение (Не A и B), чтобы определить, какое число было больше. Начните с самого значительного бита и продолжите работу с обоих байтов. Если у вас нет конструкции цикла, вручную сравните каждый бит.

реализация ", когда они бывают разные":

(A != B) и (моя логика здесь)

попробуйте это, (но имейте в виду для переполнений) (Код в C#)

    public static Int32 Maximum(params Int32[] values)
    {
        Int32 retVal = Int32.MinValue;
        foreach (Int32 i in values)
            retVal += (((i - retVal) >> 31) & (i - retVal));
        return retVal;        
    }

function Min(x,y:integer):integer;
  Var
   d:integer;
   abs:integer;
 begin
  d:=x-y;
  abs:=d*(1-2*((3*d) div (3*d+1)));
  Result:=(x+y-abs) div 2;
 end;

вы можете выразить это как ряд арифметических и побитовых операций, например:

int myabs(const int& in) {
  const int tmp = in >> ((sizeof(int) * CHAR_BIT) - 1);
  return tmp - (in ^ tmp(;
}

int mymax(int a, int b) {
    return ((a+b) + myabs(b-a)) / 2;
}

пожалуйста, посмотрите на эту программу.. это может быть лучшим ответом до даты на этой странице...

#include <stdio.h>

int main()
{
    int a,b;
    a=3;
    b=5;
    printf("%d %d\n",a,b);
    b = (a+b)-(a=b); // this line is doing the reversal
    printf("%d %d\n",a,b);
    return 0;
}

//Assuming 32 bit integers 
int is_diff_positive(int num)
{
    ((num & 0x80000000) >> 31) ^ 1; // if diff positive ret 1 else 0
}
int sign(int x)
{
   return ((num & 0x80000000) >> 31);
}

int flip(int x)
{
   return x ^ 1;
}

int max(int a, int b)
{
  int diff = a - b;

  int is_pos_a = sign(a);
  int is_pos_b = sign(b);

  int is_diff_positive = diff_positive(diff);
  int is_diff_neg = flip(is_diff_positive);

  // diff (a - b) will overflow / underflow if signs are opposite
  // ex: a = INT_MAX , b = -3 then a - b => INT_MAX - (-3) => INT_MAX + 3
  int can_overflow = is_pos_a ^ is_pos_b;
  int cannot_overflow = flip(can_overflow);
  int res = (cannot_overflow * ( (a * is_diff_positive) + (b * 
            is_diff_negative)) + (can_overflow * ( (a * is_pos_a) + (b * 
            is_pos_b)));

  return res;

}

Это зависит от того, какой язык вы используете, но Тернарный Оператор может быть полезно.

но тогда, если вы не можете выполнять условные проверки в своем "скриптовом приложении", у вас, вероятно, нет троичного оператора.

если A всегда больше B .. [ можно использовать] .. MAX = (A - B) + B;

нет необходимости. Просто используйте:int maxA(int A, int B){ return A;}

(1) Если условия разрешают вам делать max = a>b ? a : b.

(2) Любой другой метод либо использует определенный набор чисел, либо полагается на неявные условные проверки.

(2а) max = a-((a-b)&((a-b)>>31)) это аккуратно, но это работает только if вы используете 32-битные числа. Вы можете развернуть его произвольным большим числом N, но метод потерпит неудачу, если вы пытаетесь найти max (N-1, N+1). Этот алгоритм работает для автоматов конечного состояния, но не для машины Тьюринга.

(2b) величина |a-b| условие |a-b| = a-b>0 a-b : b-a

о:

квадратный корень также является условием. Всякий раз, когда c>0 и c^2 = d у нас есть второе решение -c, потому что (-c)^2 = (-1)^2*c^2 = 1*c^2 = d. Квадратный корень возвращает наибольшее значение в паре. Я поставляется со сборкой в int max(int c1, int c2){return max(c1, c2);}

без сравнения операторная математика очень симметрична, а также ограничена по мощности. Положительные и отрицательные числа нельзя различить без if что-то в этом роде.

#region GetMaximumNumber
/// <summary>
/// Provides method to get maximum values.
/// </summary>
/// <param name="values">Integer array for getting maximum values.</param>
/// <returns>Maximum number from an array.</returns>
private int GetMaximumNumber(params int[] values)
{
  // Declare to store the maximum number.
  int maximumNumber = 0;
  try
  {
    // Check that array is not null and array has an elements.
    if (values != null &&
        values.Length > 0)
    {
      // Sort the array in ascending order for getting maximum value.
      Array.Sort(values);

      // Get the last value from an array which is always maximum.
      maximumNumber = values[values.Length - 1];
    }
  }
  catch (Exception ex)
  {
    throw ex;
  }
  return maximumNumber;
}
#endregion