Matlab-Удаление Шума Сигнала

У меня есть вектор данных, который содержит целые числа в диапазоне -20 20.

Ниже приведен график со значениями:

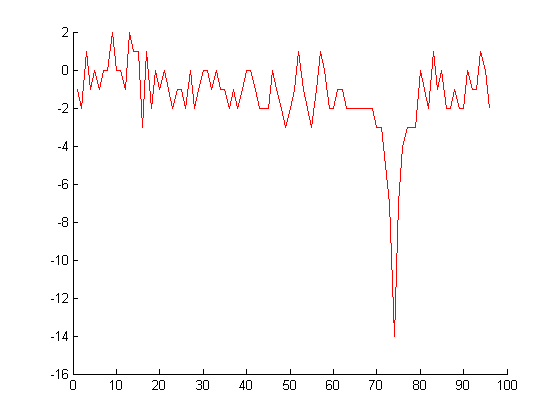
enter image description here

это выборка из 96 элементов из векторных данных. Большинство элементов расположены в интервале -2, 2, Как видно из приведенного выше графика.

Я хочу устранить шум из данных. Я хочу устранить пики низкой амплитуды и сохранить пик высокой амплитуды, а именно такие пики, как по индексу 74.

в принципе, я просто хочу увеличить контраст между пиками высокой амплитуды и пиками низкой амплитуды, и если бы можно было устранить пики низкой амплитуды.

Не могли бы вы предложить мне способ сделать это?

Я пробовал mapstd функция, но проблема в том, что она также нормализует этот пик высокой амплитуды.

Я думал об использовании инструментария вейвлет-преобразования, но я не знаю точно, как восстановите данные по коэффициентам вейвлет-декомпозиции.

можете ли вы порекомендовать мне способ сделать это?

8
matlab signal-processing wavelet

5 ответов

Если это только для демонстративных целей, и вы на самом деле не собираетесь использовать эти масштабированные значения ни для чего, мне иногда нравится увеличивать контраст следующим образом:

% your data is in variable 'a'
plot(a.*abs(a)/max(abs(a)))

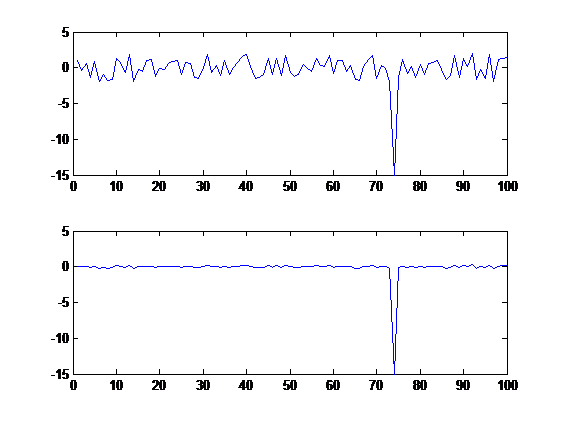
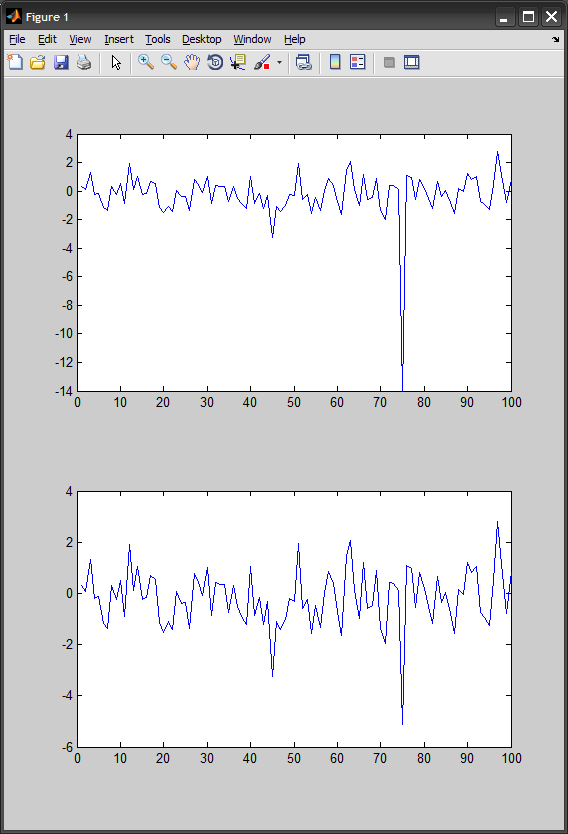
edit: поскольку мы публикуем изображения, вот мой (до/после): enter image description here

7

один подход для обнаружения выбросов-использовать правило трех стандартных отклонений. Пример:

%# some random data resembling yours
x = randn(100,1);
x(75) = -14;
subplot(211), plot(x)

%# tone down the noisy points
mu = mean(x); sd = std(x); Z = 3;
idx = ( abs(x-mu) > Z*sd );         %# outliers
x(idx) = Z*sd .* sign(x(idx));      %# cap values at 3*STD(X)
subplot(212), plot(x)

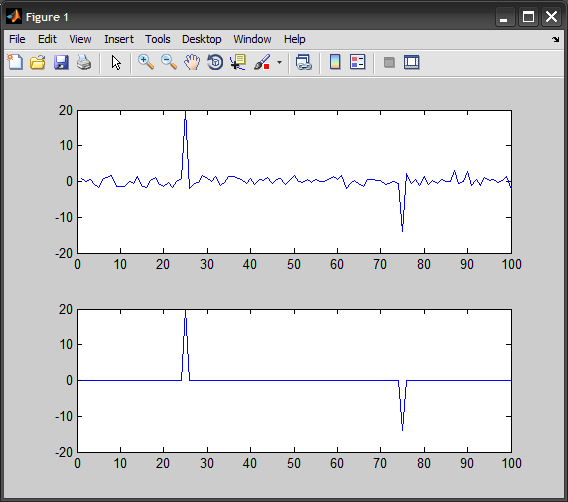
enter image description here

EDIT:

Кажется, я неправильно понял цель здесь. Если вы хотите сделать наоборот, что-то вроде этого:

%# some random data resembling yours
x = randn(100,1);
x(75) = -14; x(25) = 20;
subplot(211), plot(x)

%# zero out everything but the high peaks
mu = mean(x); sd = std(x); Z = 3;
x( abs(x-mu) < Z*sd ) = 0;
subplot(212), plot(x)

enter image description here

8

вы можете попробовать фильтр разделенного окна. Если x-ваш текущий образец, фильтр будет выглядеть примерно так:

k = [L L L L L L 0 0 0 x 0 0 0 R R R R R R]

для каждого образца x вы усредняете полосу окружающих образцов слева (L) и полосу окружающих образцов справа. Если ваши образцы положительные и отрицательные (как ваши), то вы должны принять АБС. сначала значение. Затем вы делите образец x на среднее значение этих окружающих образцов.

y[n] = x[n] / mean(abs(x([L R])))

каждый раз, когда вы делаете это пики подчеркнуты, а шум приглушен. Вы можете сделать более одного прохода, чтобы увеличить эффект. Он несколько чувствителен к выбору ширины этих полос, но может работать. Например:

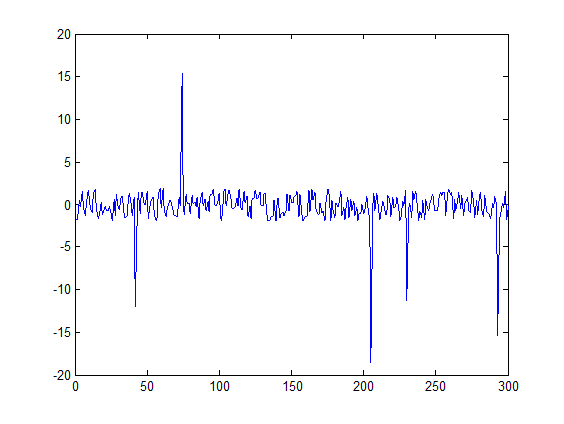
before

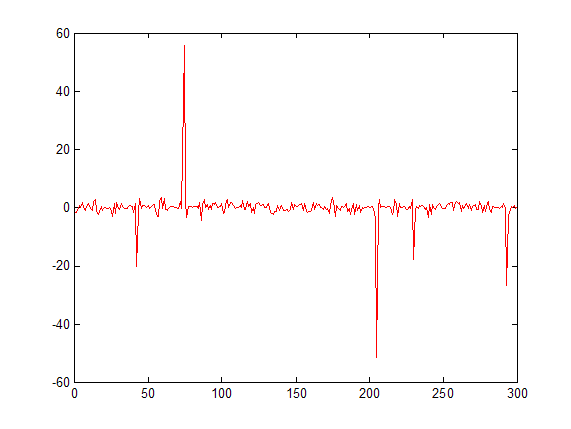
два прохода:

after

6

на самом деле вам нужно какое-то сжатие для масштабирования ваших данных, то есть: значения между -2 и 2 масштабируются определенным фактором, а все остальное масштабируется другим фактором. Грубый способ сделать это - свести все малые значения к нулю, то есть

x = randn(1,100)/2; x(50) = 20; x(25) = -15; % just generating some data
threshold = 2;
smallValues = (abs(x) <= threshold);
y = x;
y(smallValues) = 0;
figure; 
plot(x,'DisplayName','x'); hold on; 
plot(y,'r','DisplayName','y'); 
legend show;

пожалуйста, не думайте, что это очень нелинейная операция (например, когда вы хотите пики, оцененные в 2.1 и 1.9, они будут производить совсем другое поведение: один будет удален, другой будет хранившийся.) Поэтому для показа, это может быть все, что вам нужно, для дальнейшей обработки, это может зависеть от того, что вы пытаетесь сделать.

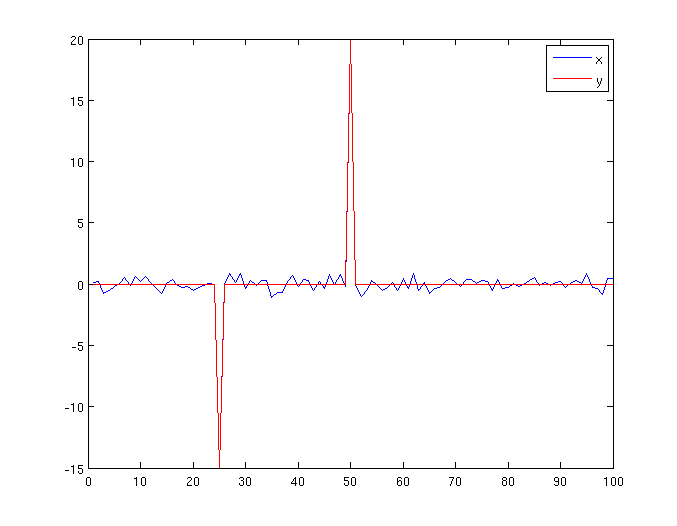
enter image description here

3

чтобы устранить пики низкой амплитуды, вы собираетесь приравнять весь сигнал низкой амплитуды к шуму и игнорировать.

Если у вас есть какие-либо знания априори, просто используйте его.

если ваш сигнал a, то

a(abs(a)<X) = 0

где X-максимальный ожидаемый размер шума.

Если вы хотите получить фантазии и найти это "на лету", то используйте kmeans 3. Это в наборе инструментов статистики, здесь:

http://www.mathworks.com/help/toolbox/stats/kmeans.html

кроме того, вы можете использовать метод Otsu для абсолютных значений данных и использовать знак назад.

обратите внимание, что эти и все другие методы, которые я видел в этом потоке, предполагают, что вы выполняете постобработку. Если вы делаете эту обработку в режиме реального времени, все должно измениться.

2