Множеством выходов гауссовского процесса регрессии в пакет scikit-учиться
Я использую пакет scikit узнать для операции регрессии гауссовского процесса (GPR) для прогнозирования данных. Мои данные обучения следующие:
x_train = np.array([[0,0],[2,2],[3,3]]) #2-D cartesian coordinate points
y_train = np.array([[200,250, 155],[321,345,210],[417,445,851]]) #observed output from three different datasources at respective input data points (x_train)
тестовые точки (2-D), где среднее и дисперсия/стандартное отклонение должны быть предсказаны:
xvalues = np.array([0,1,2,3])
yvalues = np.array([0,1,2,3])
x,y = np.meshgrid(xvalues,yvalues) #Total 16 locations (2-D)
positions = np.vstack([x.ravel(), y.ravel()])
x_test = (np.array(positions)).T
теперь, после запуска GPR (GausianProcessRegressor) fit (здесь продукт ConstantKernel и RBF используется в качестве ядра в GaussianProcessRegressor), среднее и отклонение / стандартное отклонение можно предсказать, следуя линии код:
y_pred_test, sigma = gp.predict(x_test, return_std =True)
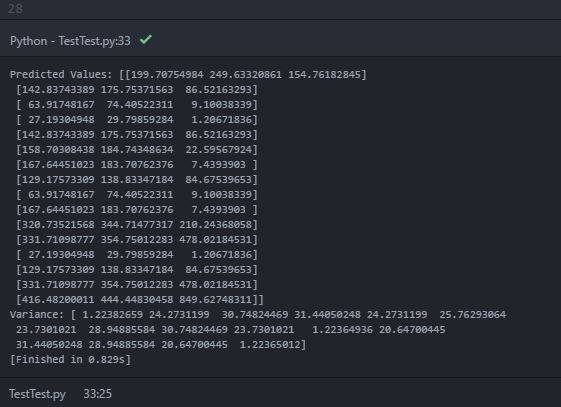
при печати прогнозируемого среднего (y_pred_test) и дисперсии (sigma), Я получаю следующий вывод, напечатанный в консоли:
в прогнозируемых значениях (среднее значение) печатается "вложенный массив" с тремя объектами внутри внутреннего массива. Можно предположить, что внутренние массивы являются предсказанными средними значениями каждого источника данных в каждой 2-D точке тестирования. Однако напечатанное отклонение содержит только одно массив из 16 объектов (возможно, для 16 точек проверки). Я знаю, что дисперсия дает указание на неопределенность оценки. Следовательно, я ожидал предсказанной дисперсии для каждого источника данных в каждой тестовой точке. Мои ожидания ошибочны? Как получить прогнозируемую дисперсию для каждого источника данных в каждой тестовой точке? Это из-за неправильного кода?
спасибо!
2 ответов
Ну, вы случайно наткнулись на айсберг...
в качестве прелюдии давайте проясним, что понятия дисперсии и стандартного отклонения определяются только для скаляр переменные; для векторных переменных (например, ваш собственный 3d-выход здесь) понятие дисперсии больше не имеет смысла, а матрица ковариации используется (Википедия, Вольфрам).
продолжая прелюдию, форма ваш sigma действительно, как и ожидалось в соответствии с scikit-learn docs на predict метод (т. е. нет кодирование ошибка в вашем случае):
возвращает:
y_mean : array, shape = (n_samples, [n_output_dims])
среднее предиктивного распределения точек запроса
y_std : array, shape = (n_samples,), необязательно
стандартное отклонение прогнозного распределения в точках запроса. Возвращается, только если return_std имеет значение True.
y_cov : array, shape = (n_samples, n_samples), необязательно
ковариация совместного предсказательного распределения точек запроса. Возвращается, только если return_cov имеет значение True.
в сочетании с моим предыдущим замечанием о ковариационной матрице первым выбором было бы попробовать predict функция с аргументом return_cov=True вместо этого (с момента запроса дисперсия векторной переменной бессмысленно); но опять же, это приведет к матрице 16x16 вместо матрицы 3x3 (ожидаемая форма ковариационной матрицы для 3 выходных переменных)...
уточнив эти детали, перейдем к сути вопроса.
В основе вашего вопроса лежит что-то редко (или даже намекнул) на практике и в соответствующих учебных пособий: гауссовский процесс регрессия с несколько выходов весьма нетривиальная и все еще область активных исследований. Возможно, scikit-learn действительно не может справиться с этим делом, несмотря на то, что это будет внешне выглядеть так, не выдав хотя бы какое-то соответствующее предупреждение.
давайте искать некоторые подтверждения этого утверждения в последние научная литература:
регрессия гауссовского процесса с несколькими переменными ответа (2015) - цитирую (выделено мой):
большинство реализаций GPR моделируют только одну переменную ответа, в связи с трудность формулирования ковариационной функции для коррелированные переменные множественного ответа, которые описывают не только корреляция между точками данных, но также корреляция между ответы. В документе предлагается прямая формулировка функция ковариации для мульти-ответ ППГ, основан на идее, что [...]
несмотря на высокое понимание GPR для различных задач моделирования, там все еще существуют некоторые нерешенные проблемы с методом GPR. Из особый интерес в этой статье представляет необходимость моделирования нескольких переменная отклика. традиционно одна переменная ответа рассматривается как гауссовский процесс и несколько ответов моделируются независимо без учета их соотношения. это прагматично и во многих приложениях применялся простой подход (например, [7, 26, 27]), хотя это не идеально. Ключ к моделированию множественной реакции Гауссовы процессы-это формулировка ковариационной функции, которая описывает не только корреляцию между точками данных, но и корреляция между ответами.
замечания по многовыходной гауссовой регрессии процесса (2018) - цитирование (акцент в оригинале):
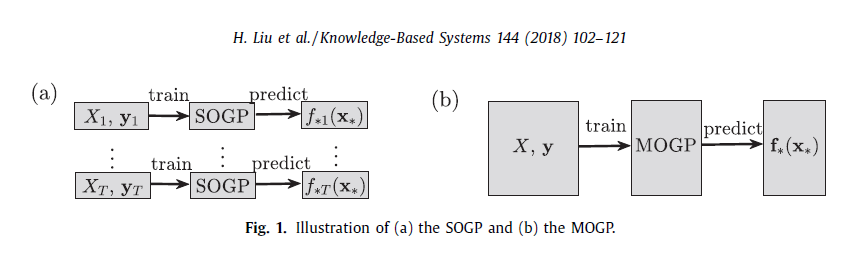
Типичный GPs обычно конструирован для сценариев одиночн-выхода при котором результатом является скаляр. Однако, проблемы multi-выхода имеют возникшие в различных областях, [...]. Предположим, что мы пытаемся аппроксимировать t выходов {f (t}, 1 ≤t ≤T , одна интуитивная идея заключается в том, чтобы использовать один выход GP(SOGP) для аппроксимации их индивидуально, используя связанные обучающие данные D(t) = { X(t), y (t)}, см. рис. 1 (a). Учитывая, что выходы каким-то образом коррелированы, моделирование их индивидуально может привести к потере ценной информации. Следовательно, увеличивая разнообразие применений инженерства приступая к использованию многовыходного GP (MOGP), который концептуально изображен на рис. 1 (b), для суррогатного моделирования.
изучение MOGP имеет длинную историю и как multivariate Кригинг или ко-Кригинг в геостатистическом сообществе; [...] MOGP обрабатывает проблемы с основным предположением, что выходы каким-то образом коррелированы. Следовательно, ключевой проблемой в MOGP является эксплуатируйте корреляции выхода такие что выходы могут использовать информацию от одного другой для того, чтобы обеспечить более точные прогнозы по сравнению с моделированием их по отдельности.
основанные на физике Ковариационные модели для гауссовых процессов с несколькими выходами (2013) - цитирую:
гауссовский анализ процессов с множественными выходами ограничено тем, что гораздо меньше хороших классов ковариации функции существуют по сравнению со скалярными случай (одиночн-выхода). [...]
трудность поиска "хороших" ковариационных моделей для нескольких результаты могут иметь важные практические последствия. Неправильный структура ковариационной матрицы может значительно уменьшить эффективность процесса количественной оценки неопределенности, а также прогноз эффективности в выводах кригинга [16]. Поэтому мы спорим, ковариационная модель может играть еще более глубокую роль в совместном кригинге [7, 17]. Этот аргумент применяется, когда структура ковариации выводится из данных, как это обычно бывает.
следовательно, мое понимание, как я уже сказал, заключается в том, что sckit-learn действительно не способен обрабатывать такие случаи, несмотря на то, что нечто подобное не упоминается или не намекается в документации (может быть интересно открыть соответствующий вопрос на странице проекта). Кажется, это заключение в это актуально так нити тоже, как и в этот CrossValidated thread относительно набора инструментов GPML (Matlab).
сказав это, и помимо возврата к выбору простого моделирования каждого выхода отдельно (не недопустимый выбор, если вы помните, что вы можете выбрасывать полезную информацию из корреляции между вашими 3-D выходными элементами), есть по крайней мере один набор инструментов Python, который, кажется, способен моделировать GPS с несколькими выходами, а именно runlmc (статьи, код, документация).
прежде всего, если используемый параметр "Сигма", это относится к стандартному отклонению, а не к дисперсии (напомним, дисперсия-это просто квадрат стандартного отклонения).
легче осмыслить через дисперсии, так как дисперсия определяется как Евклидово расстояние от точки данных до среднего набора.
в вашем случае, у вас есть набор 2D точек. Если вы считаете их точками на 2D-плоскости, то дисперсия - это просто расстояние от каждой точки до среднего. Стандартное отклонение, чем было бы положительным корнем дисперсии.
в этом случае у вас есть 16 тестовых точек и 16 значений стандартного отклонения. Это имеет смысл, так как каждая тестовая точка имеет свое собственное определенное расстояние от среднего значения набора.
Если вы хотите вычислить дисперсию набора точек, вы можете сделать это, суммируя дисперсию каждой точки по отдельности, деля ее на количество точек, а затем вычитая среднее квадратное значение. Позитив корень этого числа даст стандартное отклонение множества.
в сторону: это также означает, что если вы измените набор путем вставки, удаления или замены, стандартное отклонение каждой точки изменится. Это связано с тем, что среднее значение будет пересчитано для размещения новых данных. Этот итерационный процесс является фундаментальной силой кластеризации k-средних.