Найдите точку, заданное расстояние, вдоль простой кубической кривой Безье. (На iPhone!)
представьте, что у вас есть совершенно нормальная четырехточечная кривая Безье (две точки и две контрольные точки), созданная с помощью curveToPoint:controlPoint1:controlPoint2: в вашем приложении cocoa:
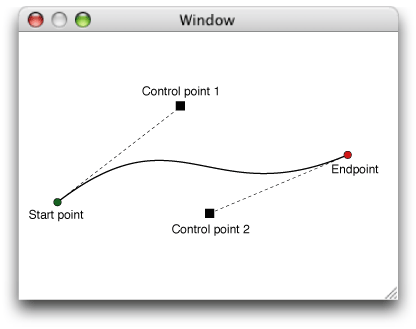
Как вы находите точки (и касательные), вдоль кривой?
позже: для полный, упрощенный, решением основываясь на ответе Михала ниже, нажмите на:
найти касательную точки На кубической кривой Безье (на iPhone)
и просто скопируйте и вставьте код из: https://stackoverflow.com/a/31317254/294884
3 ответов
есть простая математика для вычисления позиций, вы можете прочитать об этом в каждой статье, обсуждающей кривые Безье, даже в Википедии. В любом случае, я могу относиться ко всем, кто в беде, чтобы фактически реализовать его в коде, поэтому я написал этот образец UIView, поскольку это, вероятно, самый простой способ начать работу.
#import "MBBezierView.h"
CGFloat bezierInterpolation(CGFloat t, CGFloat a, CGFloat b, CGFloat c, CGFloat d) {
CGFloat t2 = t * t;
CGFloat t3 = t2 * t;
return a + (-a * 3 + t * (3 * a - a * t)) * t
+ (3 * b + t * (-6 * b + b * 3 * t)) * t
+ (c * 3 - c * 3 * t) * t2
+ d * t3;
}
@implementation MBBezierView
- (void)drawRect:(CGRect)rect {
CGPoint p1, p2, p3, p4;
p1 = CGPointMake(30, rect.size.height * 0.33);
p2 = CGPointMake(CGRectGetMidX(rect), CGRectGetMinY(rect));
p3 = CGPointMake(CGRectGetMidX(rect), CGRectGetMaxY(rect));
p4 = CGPointMake(-30 + CGRectGetMaxX(rect), rect.size.height * 0.66);
[[UIColor blackColor] set];
[[UIBezierPath bezierPathWithRect:rect] fill];
[[UIColor redColor] setStroke];
UIBezierPath *bezierPath = [[[UIBezierPath alloc] init] autorelease];
[bezierPath moveToPoint:p1];
[bezierPath addCurveToPoint:p4 controlPoint1:p2 controlPoint2:p3];
[bezierPath stroke];
[[UIColor brownColor] setStroke];
for (CGFloat t = 0.0; t <= 1.00001; t += 0.05) {
CGPoint point = CGPointMake(bezierInterpolation(t, p1.x, p2.x, p3.x, p4.x), bezierInterpolation(t, p1.y, p2.y, p3.y, p4.y));
UIBezierPath *pointPath = [UIBezierPath bezierPathWithArcCenter:point radius:5 startAngle:0 endAngle:2*M_PI clockwise:YES];
[pointPath stroke];
}
}
@end
вот что я получил:

приближение, что t-расстояние вдоль кривой, которую предлагает Михал, может быть затруднительным с некоторыми кривыми и для некоторых целей. К сожалению, я довольно долго искал без везения для реализации Obj-C правильного решения.
решение, однако, описано довольно фантастическим образом Майком "Pomax" Kamermans в его удивительном праймер на кривых Безье. Он даже имеет весь код, написанный в обработке и в общественном достоянии. Я удивительно, что никто еще не преобразовал это в Obj-C. Очень соблазнительно.
любой Beziér кривая может быть просто рассматривать как полиномиальные функции с векторными или комплексными коэффициентами. Кубическая кривая Безьера, такая как на вашем скриншоте, будет генерироваться полиномиальной функцией порядка 3, и каждая точка на кривой описывает результат B (t) полинома кривой, вычисленного для определенного входного значения t. Если я не ошибаюсь, как только вы узнаете полином, используемый для создания кривой, вы можете просто решить для B (t) = a+bi, где a+bi описывает точку на комплексной плоскости, которую вы хотите найти t значение. Поиск корней в таких многочленах является хорошо понятной задачей и может быть решен алгебраически для кривых порядка 2 или ниже и с использованием некоторого метода, такого как форвард-Ньютон для многочленов более высокой степени. Если вы знаете производящий полином, конечно, также должно быть очень просто найти производные. Beziér обычно черпаются из "шаблона полиномов" где изменяются только коэффициенты, когда рисуется другая кривая, поэтому вы можете найти ее где-нибудь в документации.
