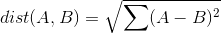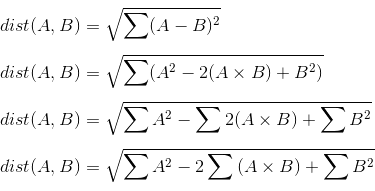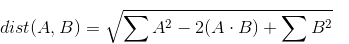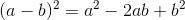Numpy Broadcast для выполнения векторизации евклидова расстояния

вот исходные входные переменные:

A = np.array([[1,1,1,1],[2,2,2,2]])
B = np.array([[1,2,3,4],[1,1,1,1],[1,2,1,9]])
A
# array([[1, 1, 1, 1],
#        [2, 2, 2, 2]])
B
# array([[1, 2, 3, 4],
#        [1, 1, 1, 1],
#        [1, 2, 1, 9]])

a-массив 2x4. B-массив 3x4.

мы хотим вычислить операцию евклидовой матрицы расстояний в одной полностью векторизованной операции, где dist[i,j] содержит расстояние между I-м экземпляром в A и J-м экземпляром в B. So dist в этом примере 2x3.

на расстояние

может быть якобы написано с numpy as

dist = np.sqrt(np.sum(np.square(A-B))) # DOES NOT WORK
# Traceback (most recent call last):
#   File "<stdin>", line 1, in <module>
# ValueError: operands could not be broadcast together with shapes (2,4) (3,4)

однако, как показано выше, проблема заключается в том, что операция вычитания A-B включает несовместимые размеры массива, в частности 2 и 3 в первом измерении.

A has dimensions 2 x 4
B has dimensions 3 x 4

чтобы сделать элементарное вычитание, мы должны заполнить либо A, либо B, чтобы удовлетворить правила трансляции numpy. Я выберу pad A с дополнительным измерением, чтобы он стал 2 x 1 x 4, что позволяет измерениям массивов выстраиваться в линию для трансляции. Для большего numpy вещания, см учебник в руководстве scipy и последний пример в в этом уроке.

вы можете выполнить прокладку с np.newaxis или с . Я показываю оба ниже:

# First approach is to add the extra dimension to A with np.newaxis
A[:,np.newaxis,:] has dimensions 2 x 1 x 4
B has dimensions                     3 x 4

# Second approach is to reshape A with np.reshape
np.reshape(A, (2,1,4)) has dimensions 2 x 1 x 4
B has dimensions                          3 x 4

как вы можете видеть, использование любого подхода позволит измерениям выровняться. Я буду использовать первый подход с np.newaxis. Итак, теперь это будет работать для создания A - B, который является 2x3x4 массив:

diff = A[:,np.newaxis,:] - B
# Alternative approach:
# diff = np.reshape(A, (2,1,4)) - B
diff.shape
# (2, 3, 4)

теперь мы можем поместить это выражение различия в dist утверждение уравнения, чтобы получить окончательный результат:

dist = np.sqrt(np.sum(np.square(A[:,np.newaxis,:] - B), axis=2))
dist
# array([[ 3.74165739,  0.        ,  8.06225775],
#        [ 2.44948974,  2.        ,  7.14142843]])

отметим, что sum над axis=2, что означает взять сумму по третьей оси массива 2x3x4 (где идентификатор оси начинается с 0).

если ваши массивы малы, то вышеуказанная команда будет работать просто отлично. Однако, если у вас есть большие массивы, вы можете столкнуться с проблемами памяти. Обратите внимание, что в приведенном выше примере, numpy внутренне создал массив 2x3x4 для выполнения трансляции. Если мы обобщим A, чтобы иметь размеры a x z и B, чтобы иметь размеры b x z, тогда numpy внутренне создаст a x b x z массив для радиовещания.

мы можем избежать создания этого промежуточного массива, выполнив некоторые математические манипуляции. Поскольку вы вычисляете евклидово расстояние как сумму квадратов разностей, мы можем воспользоваться математическим фактом, что сумма квадратов разностей может быть переписанный.

обратите внимание, что средний срок включает в себя сумму более элемент-мудрый умножение. Эта сумма за multiplcations более известный как скалярное произведение. Поскольку A и B-каждая матрица, то эта операция на самом деле является матричным умножением. Таким образом, мы можем переписать, как:

затем мы можем написать следующий numpy код:

threeSums = np.sum(np.square(A)[:,np.newaxis,:], axis=2) - 2 * A.dot(B.T) + np.sum(np.square(B), axis=1)
dist = np.sqrt(threeSums)
dist
# array([[ 3.74165739,  0.        ,  8.06225775],
#        [ 2.44948974,  2.        ,  7.14142843]])

обратите внимание, что ответ выше точно такой же, как и в предыдущей реализации. Опять же, преимущество здесь заключается в том, что нам не нужно создавать промежуточный массив 2x3x4 для вещания.

для полноты, давайте дважды проверим, что размеры каждого слагаемого в threeSums разрешена трансляция.

np.sum(np.square(A)[:,np.newaxis,:], axis=2) has dimensions 2 x 1
2 * A.dot(B.T) has dimensions                               2 x 3
np.sum(np.square(B), axis=1) has dimensions                 1 x 3

Итак, как и ожидалось, заключительный dist массив имеет размеры 2x3.

это использование точечного продукта вместо суммы элементарное умножение также обсуждается в в этом уроке.

недавно у меня была такая же проблема с deep learning (stanford cs231n, Assignment1), но когда я использовал

 np.sqrt((np.square(a[:,np.newaxis]-b).sum(axis=2)))

произошла ошибка

MemoryError

это означает, что у меня закончилась память(на самом деле, это произвело массив 500*5000*1024 в середине.Он такой огромный!)

чтобы предотвратить эту ошибку,мы можем использовать формулы для упрощения:

код:

import numpy as np
aSumSquare = np.sum(np.square(a),axis=1);
bSumSquare = np.sum(np.square(b),axis=1);
mul = np.dot(a,b.T);
dists = np.sqrt(aSumSquare[:,np.newaxis]+bSumSquare-2*mul)

эта функция уже включена в пространственный модуль сципи и я рекомендую использовать его, поскольку он будет векторизован и оптимизирован под капотом. Но, как видно из другого ответа, есть способы сделать это самостоятельно.

import numpy as np
a = np.array([[1,1,1,1],[2,2,2,2]])
b = np.array([[1,2,3,4],[1,1,1,1],[1,2,1,9]])
np.sqrt((np.square(a[:,np.newaxis]-b).sum(axis=2)))
# array([[ 3.74165739,  0.        ,  8.06225775],
#       [ 2.44948974,  2.        ,  7.14142843]])
from scipy.spatial.distance import cdist
cdist(a,b)
# array([[ 3.74165739,  0.        ,  8.06225775],
#       [ 2.44948974,  2.        ,  7.14142843]])

используя numpy.linalg.норма!--4--> также хорошо работает с вещания. Указание целочисленного значения для axis будет использовать векторную норму, которая по умолчанию является евклидовой нормой.

import numpy as np

a = np.array([[1,1,1,1],[2,2,2,2]])
b = np.array([[1,2,3,4],[1,1,1,1],[1,2,1,9]])
np.linalg.norm(a[:, np.newaxis] - b, axis = 2)

# array([[ 3.74165739,  0.        ,  8.06225775],
#       [ 2.44948974,  2.        ,  7.14142843]])