Обход Графа C#
этот алгоритм отлично справляется с обходом узлов на графике.
Dictionary<Node, bool> visited = new Dictionary<Node, bool>();
Queue<Node> worklist = new Queue<Node>();
visited.Add(this, false);
worklist.Enqueue(this);
while (worklist.Count != 0)
{
Node node = worklist.Dequeue();
foreach (Node neighbor in node.Neighbors)
{
if (!visited.ContainsKey(neighbor))
{
visited.Add(neighbor, false);
worklist.Enqueue(neighbor);
}
}
}
Я могу использовать это, чтобы найти целевой узел в графе. В извлекает список (или соз) элементы рабочего списка обрабатывается. Как только я найду цель, как я могу вернуть полный путь к узлу?
обновление Я пытаюсь понять, как изменить путь к корню. Метод вызывается на корневом узле, после этого у детей может быть два родителя, поэтому он не является так же просто, как вызов родительского свойства на каждом узле и перемещение обратно.
цель метода-найти путь, а не перебирать все узлы или проверить, существует ли узел.
5 ответов
следите за узлами предшественника. В простой реализации, это словарь, и обычно обозначается как π в псевдо-код:
Dictionary<Node, bool> visited = new Dictionary<Node, bool>();
Dictionary<Node, Node> π = new Dictionary<Node, Node>();
Queue<Node> worklist = new Queue<Node>();
visited.Add(this, false);
worklist.Enqueue(this);
while (worklist.Count != 0)
{
Node node = worklist.Dequeue();
foreach (Node neighbor in node.Neighbors)
{
if (!visited.ContainsKey(neighbor))
{
visited.Add(neighbor, false);
π.Add(neighbor, node);
worklist.Enqueue(neighbor);
}
}
}
затем вы можете перебирать эти предшественники, чтобы отследить путь от любого узла, скажем e:
while (π[e] != null) {
Console.WriteLine(e);
e = π[e];
}
Я попытался использовать этот фрагмент, чтобы получить альтернативные пути от вершины (вершины в моем коде), используя источник и судьбу, но просто не работает...
public String EncontrarMenorCaminho(Vertice o, Vertice d)
{
Dictionary<Vertice, bool> visited = new Dictionary<Vertice, bool>();
Dictionary<Vertice, Vertice> previous = new Dictionary<Vertice, Vertice>();
Queue<Vertice> worklist = new Queue<Vertice>();
String operacao = "Registro de operações realizadas:\r\n\r\n";
visited.Add(o, false);
worklist.Enqueue(o);
while (worklist.Count != 0)
{
Vertice v = worklist.Dequeue();
foreach (Vertice neighbor in EncontrarVizinhos(v))
{
if (!visited.ContainsKey(neighbor))
{
visited.Add(neighbor, false);
previous.Add(neighbor, v);
worklist.Enqueue(neighbor);
}
}
}
if (previous.Count > 0)
{
for (int p = 0; p < previous.Count; p++)
{
Vertice v1 = previous.ElementAt(p).Key;
Vertice v2 = previous.ElementAt(p).Value;
EncontrarAresta(v1, v2).Selecionado = true;
EncontrarAresta(v2, v1).Selecionado = true;
operacao += v1.Info.ToString() + "x" + v2.Info.ToString() + "\r\n";
}
}
List<Vertice> grupos = new List<Vertice>();
foreach (Aresta a in ArestasSelecionadas())
{
if (!grupos.Contains(a.Origem)) grupos.Add(a.Origem);
}
foreach (Vertice v in grupos)
{
int menorpeso = this.infinito;
foreach(Vertice vz in EncontrarVizinhos(v))
{
Aresta tmp = EncontrarAresta(v,vz);
if (tmp.Selecionado == true && tmp.Peso < menorpeso)
{
menorpeso = tmp.Peso;
}
else
{
tmp.Selecionado = false;
}
}
}
DesenharMapa();
return operacao;
в основном операция получает все отмеченные ребра (Selecionado = true) и проверяет снова, если необходимо продолжить выбор...
в этом примере я хочу получить кратчайший путь от vertext 'N' до вершины 'Q':
см. предварительный просмотр изображения здесь:
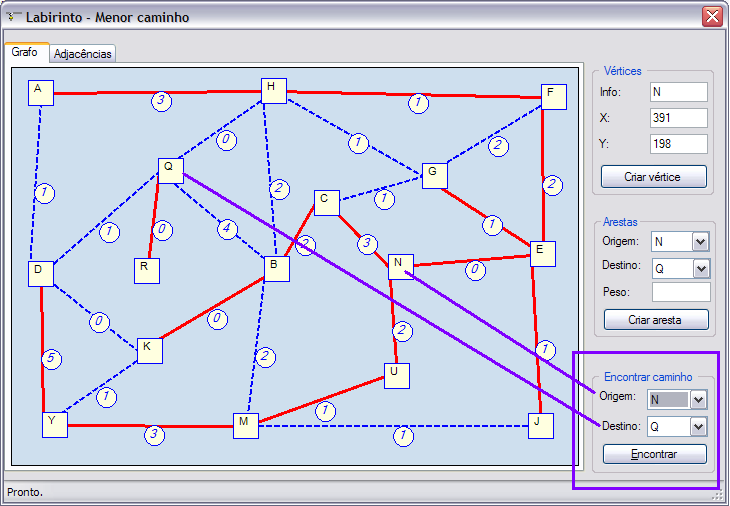
является ли" это", то есть текущий экземпляр," корнем " графика, если такая вещь существует?
является ли граф циклическим или ациклическим? Боюсь, я не знаю всех терминов для теории графов.
вот что мне действительно интересно:
A -> B -> C ------> F
B -> D -> E -> F
вот мои вопросы:
- это произойдет?
- может ли "это" в вашем коде когда-либо начинаться с B?
- каким будет путь к F?
если график никогда не соединяется вместе, когда он разделился, не содержит циклов, и "это" всегда будет корнем/началом графика, простой словарь будет обрабатывать путь.
Dictionary<Node, Node> PreNodes = new Dictionary<Node, Node>();
для каждого узла, который вы посещаете, добавьте соседний узел в качестве ключа, а узел был соседом в качестве значения. Это позволит вам, как только вы найдете целевой узел, вернуться назад, чтобы получить обратный путь.
другими словами, словарь для графика выше, после полного пересечение будет:
B: A
C: B
D: B
E: D
F: C (or E, or both?)
чтобы найти путь к E-узлу, просто вернитесь:
E -> D -> B -> A
который дает вам путь:
A -> B -> D -> E
поскольку вы не отслеживаете путь к "текущему" узлу во все времена, вам придется построить это, когда вы найдете цель. Если ваш класс узла имеет родительское свойство, вы можете легко отследить дерево, чтобы построить полный путь.
Питер почти прав. Я не думаю, что вы можете сохранить ссылку на родительскую вершину в классе node, потому что она изменяется в зависимости от вершины, с которой вы начинаете свой первый поиск ширины. Вам нужно создать родительский словарь с ключами, являющимися узлами, и значениями, являющимися родительскими узлами. Когда вы посещаете каждую вершину (но перед обработкой), вы добавляете родителей в словарь. Затем вы можете подняться по родительскому пути обратно к корневой вершине.
