Обнаружение центра и угла прямоугольников в изображении с помощью Opencv
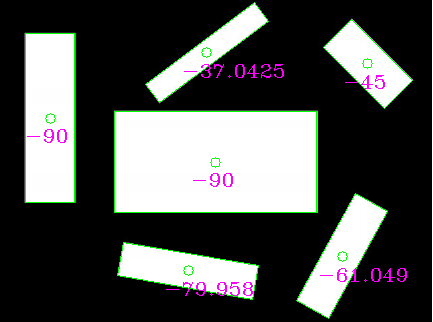
У меня есть изображение, как показано ниже :
Мне нужно узнать количество прямоугольников, центр каждого прямоугольника и измерить угол между осью, параллельной более длинному краю прямоугольника, проходящего через центр, и измерить угол в направлении против часовой стрелки от горизонтали.Я выяснил количество прямоугольников на изображении.Я поражен, обнаружив центр и угол отражения.Найти центр через мгновения-это не давая мне правильного ответа.
мой код :
import cv2
import numpy as np
import sys
img = cv2.imread(str(sys.argv[1]),0)
ret,thresh = cv2.threshold(img,127,255,0)
contours,hierarchy = cv2.findContours(thresh,1,2)
for contour in contours:
area = cv2.contourArea(contour)
if area>100000:
contours.remove(contour)
cnt = contours[0]
epsilon = 0.02*cv2.arcLength(cnt,True)
approx = cv2.approxPolyDP(cnt,epsilon,True)
print 'No of rectangles',len(approx)
#finding the centre of the contour
M = cv2.moments(cnt)
cx = int(M['m10']/M['m00'])
cy = int(M['m01']/M['m00'])
print cx,cy
3 ответов
вот как вы можете сделать это с помощью функции minAreaRect openCV. Он написан на C++ , но, вероятно, вы можете легко адаптироваться, так как использовались почти только функции OpenCV.
cv::Mat input = cv::imread("../inputData/rectangles.png");
cv::Mat gray;
cv::cvtColor(input,gray,CV_BGR2GRAY);
// since your image has compression artifacts, we have to threshold the image
int threshold = 200;
cv::Mat mask = gray > threshold;
cv::imshow("mask", mask);
// extract contours
std::vector<std::vector<cv::Point> > contours;
cv::findContours(mask, contours, CV_RETR_EXTERNAL, CV_CHAIN_APPROX_NONE);
for(int i=0; i<contours.size(); ++i)
{
// fit bounding rectangle around contour
cv::RotatedRect rotatedRect = cv::minAreaRect(contours[i]);
// read points and angle
cv::Point2f rect_points[4];
rotatedRect.points( rect_points );
float angle = rotatedRect.angle; // angle
// read center of rotated rect
cv::Point2f center = rotatedRect.center; // center
// draw rotated rect
for(unsigned int j=0; j<4; ++j)
cv::line(input, rect_points[j], rect_points[(j+1)%4], cv::Scalar(0,255,0));
// draw center and print text
std::stringstream ss; ss << angle; // convert float to string
cv::circle(input, center, 5, cv::Scalar(0,255,0)); // draw center
cv::putText(input, ss.str(), center + cv::Point2f(-25,25), cv::FONT_HERSHEY_COMPLEX_SMALL, 1, cv::Scalar(255,0,255)); // print angle
}
в результате этого изображения:
как вы можете видеть, углы, вероятно, не то, что вы хотите (потому что они случайно использовать больше или меньше строки в качестве ссылки). Вместо этого вы можете извлечь более длинные стороны прямоугольников и вычислить угол вручную.
Если вы выбираете более длинный край повернутых прямых и вычисляете угол от него, это выглядит так:
// choose the longer edge of the rotated rect to compute the angle
cv::Point2f edge1 = cv::Vec2f(rect_points[1].x, rect_points[1].y) - cv::Vec2f(rect_points[0].x, rect_points[0].y);
cv::Point2f edge2 = cv::Vec2f(rect_points[2].x, rect_points[2].y) - cv::Vec2f(rect_points[1].x, rect_points[1].y);
cv::Point2f usedEdge = edge1;
if(cv::norm(edge2) > cv::norm(edge1))
usedEdge = edge2;
cv::Point2f reference = cv::Vec2f(1,0); // horizontal edge
angle = 180.0f/CV_PI * acos((reference.x*usedEdge.x + reference.y*usedEdge.y) / (cv::norm(reference) *cv::norm(usedEdge)));
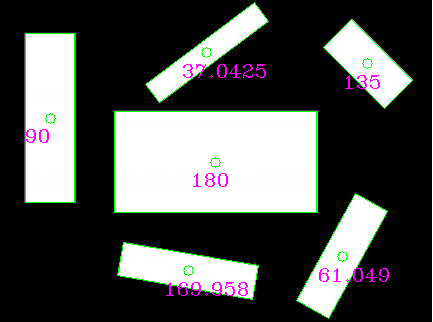
давая этот результат, который должен быть тем, что вы ищете!
EDIT: похоже, op не использует входное изображение, которое он опубликовал, потому что центры ссылочных прямоугольников будут находиться вне изображения.
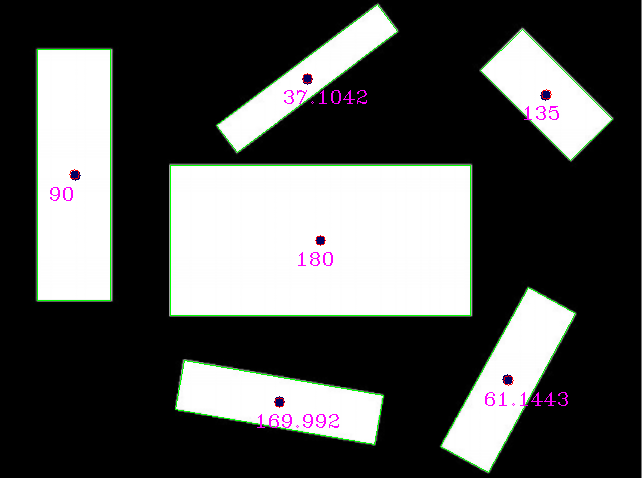
используя этот вход (вручную масштабируется, но, вероятно, все еще нет optimal):
Я получаю эти результаты (синие точки являются ссылочными центрами прямоугольника, предоставляемыми op):
сравнение ссылки с обнаружениями:
reference (x,y,angle) detection (x,y,angle)
(320,240,0) (320, 240, 180) // angle 180 is equal to angle 0 for lines
(75,175,90) (73.5, 174.5, 90)
(279,401,170) (279.002, 401.824, 169.992)
(507,379,61) (507.842, 379.75, 61.1443)
(545,95,135) (545.75, 94.25, 135)
(307,79,37) (306.756, 77.8384, 37.1042)
Я хотел бы увидеть реальное входное изображение, хотя, возможно, результат будет еще лучше.
вот как вы можете сделать это:
- маркировка подключенного компонента для обнаружения каждого шаблона (в вашем случае прямоугольников)
- разделите шаблоны в разных изображениях
- (необязательно) если шаблон не все прямоугольники, то используйте индексы формы, чтобы различать их
- вычислить основную ось с помощью анализа основных компонентов (PCA), это даст вам угол, который вы ищете.
approx = cv2.approxPolyDP (cnt,epsilon,True) создает аппроксимированный многоугольник заданного замкнутого контура. Сегменты линий в полигоне имеют переменную длину, что приводит к неправильному вычислению момента, поскольку он ожидает, что точки будут выбраны из регулярной сетки, чтобы дать вам правильный центр.
есть три решения вашей проблемы:
- используйте моменты исходных контуров перед вызовом метода аппроксимации полигона.
- использовать drawContours для создания маски областей внутри каждого замкнутого контура, а затем использовать моменты сгенерированной маски для вычисления центра.
- примеры точек на единичном расстоянии вдоль каждого сегмента линии вашего замкнутого многоугольника и используйте результирующие коллекции точек для вычисления моментов самостоятельно. Это должно дать вам тот же самый центр.