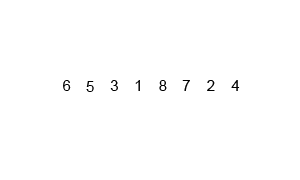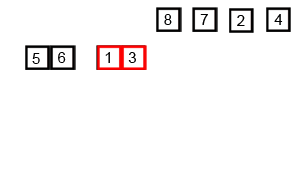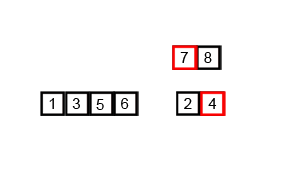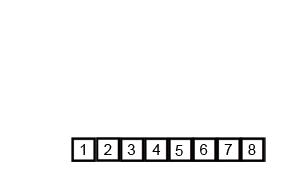Объяснение сортировки слияния для чайников
Я нашел этот код на сайте:
def merge(left, right):
result = []
i ,j = 0, 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:]
result += right[j:]
return result
def mergesort(list):
if len(list) < 2:
return list
middle = len(list) / 2
left = mergesort(list[:middle])
right = mergesort(list[middle:])
return merge(left, right)
он работает 100% , когда я его запускаю. Я просто не понимаю, как работает сортировка слиянием или как рекурсивная функция может правильно упорядочивать как левый, так и правый.
8 ответов
Я считаю, что ключом к пониманию сортировки слияния является понимание следующего принципа - Я назову его принципом слияния:
учитывая два отдельных списка A и B, упорядоченных от наименьшего до наибольшего, создайте список C, многократно сравнивая наименьшее значение A с наименьшим значением B, удаляя меньшее значение и добавляя его в C. Когда один список исчерпан, добавьте оставшиеся элементы в другом списке на C по порядку. Список C также сортируется список.
если вы поработаете над этим вручную несколько раз, вы увидите, что это правильно. Например:
A = 1, 3
B = 2, 4
C =
min(min(A), min(B)) = 1
A = 3
B = 2, 4
C = 1
min(min(A), min(B)) = 2
A = 3
B = 4
C = 1, 2
min(min(A), min(B)) = 3
A =
B = 4
C = 1, 2, 3
теперь a исчерпан, поэтому расширьте C с оставшимися значениями из B:
C = 1, 2, 3, 4
принцип слияния также легко доказать. Минимальное значение A меньше всех других значений A, а минимальное значение B меньше всех других значений B. Если минимальное значение A меньше минимального значения B, то оно также должно быть меньше все значения B. Поэтому меньше всех значений A и всех значений B.
пока вы продолжаете добавлять значение, соответствующее этим критериям, в C, вы получаете отсортированный список. Это merge выше функции.
теперь, учитывая этот принцип, очень легко понять метод сортировки, который сортирует список, разделяя его на меньшие списки, сортируя эти списки, а затем объединяя эти отсортированные списки вместе. The merge_sort функция просто функцию, которая делит список пополам, сортирует эти два списка, а затем объединяет эти два списка вместе, как описано выше.
единственный улов заключается в том, что, поскольку он рекурсивен, когда он сортирует два под-списка, он делает это, передавая их себе! Если вам трудно понять рекурсию здесь, я бы предложил сначала изучить более простые проблемы. Но если вы уже получили основы рекурсии, то все, что вам нужно понять, это то, что список из одного элемента уже сортированный. Слияние двух списков из одного элемента создает сортированный список из двух элементов; слияние двух списков из двух элементов создает сортированный список из четырех элементов; и так далее.
когда я столкнулся с трудностями, чтобы понять, как работает алгоритм, я добавляю отладочный вывод, чтобы проверить, что действительно происходит внутри алгоритма.
здесь код отладки. Попробуйте выполнить все шаги с рекурсивными вызовами mergesort и что merge делает вывод:
def merge(left, right):
result = []
i ,j = 0, 0
while i < len(left) and j < len(right):
print('left[i]: {} right[j]: {}'.format(left[i],right[j]))
if left[i] <= right[j]:
print('Appending {} to the result'.format(left[i]))
result.append(left[i])
print('result now is {}'.format(result))
i += 1
print('i now is {}'.format(i))
else:
print('Appending {} to the result'.format(right[j]))
result.append(right[j])
print('result now is {}'.format(result))
j += 1
print('j now is {}'.format(j))
print('One of the list is exhausted. Adding the rest of one of the lists.')
result += left[i:]
result += right[j:]
print('result now is {}'.format(result))
return result
def mergesort(L):
print('---')
print('mergesort on {}'.format(L))
if len(L) < 2:
print('length is 1: returning the list withouth changing')
return L
middle = len(L) / 2
print('calling mergesort on {}'.format(L[:middle]))
left = mergesort(L[:middle])
print('calling mergesort on {}'.format(L[middle:]))
right = mergesort(L[middle:])
print('Merging left: {} and right: {}'.format(left,right))
out = merge(left, right)
print('exiting mergesort on {}'.format(L))
print('#---')
return out
mergesort([6,5,4,3,2,1])
выход:
---
mergesort on [6, 5, 4, 3, 2, 1]
calling mergesort on [6, 5, 4]
---
mergesort on [6, 5, 4]
calling mergesort on [6]
---
mergesort on [6]
length is 1: returning the list withouth changing
calling mergesort on [5, 4]
---
mergesort on [5, 4]
calling mergesort on [5]
---
mergesort on [5]
length is 1: returning the list withouth changing
calling mergesort on [4]
---
mergesort on [4]
length is 1: returning the list withouth changing
Merging left: [5] and right: [4]
left[i]: 5 right[j]: 4
Appending 4 to the result
result now is [4]
j now is 1
One of the list is exhausted. Adding the rest of one of the lists.
result now is [4, 5]
exiting mergesort on [5, 4]
#---
Merging left: [6] and right: [4, 5]
left[i]: 6 right[j]: 4
Appending 4 to the result
result now is [4]
j now is 1
left[i]: 6 right[j]: 5
Appending 5 to the result
result now is [4, 5]
j now is 2
One of the list is exhausted. Adding the rest of one of the lists.
result now is [4, 5, 6]
exiting mergesort on [6, 5, 4]
#---
calling mergesort on [3, 2, 1]
---
mergesort on [3, 2, 1]
calling mergesort on [3]
---
mergesort on [3]
length is 1: returning the list withouth changing
calling mergesort on [2, 1]
---
mergesort on [2, 1]
calling mergesort on [2]
---
mergesort on [2]
length is 1: returning the list withouth changing
calling mergesort on [1]
---
mergesort on [1]
length is 1: returning the list withouth changing
Merging left: [2] and right: [1]
left[i]: 2 right[j]: 1
Appending 1 to the result
result now is [1]
j now is 1
One of the list is exhausted. Adding the rest of one of the lists.
result now is [1, 2]
exiting mergesort on [2, 1]
#---
Merging left: [3] and right: [1, 2]
left[i]: 3 right[j]: 1
Appending 1 to the result
result now is [1]
j now is 1
left[i]: 3 right[j]: 2
Appending 2 to the result
result now is [1, 2]
j now is 2
One of the list is exhausted. Adding the rest of one of the lists.
result now is [1, 2, 3]
exiting mergesort on [3, 2, 1]
#---
Merging left: [4, 5, 6] and right: [1, 2, 3]
left[i]: 4 right[j]: 1
Appending 1 to the result
result now is [1]
j now is 1
left[i]: 4 right[j]: 2
Appending 2 to the result
result now is [1, 2]
j now is 2
left[i]: 4 right[j]: 3
Appending 3 to the result
result now is [1, 2, 3]
j now is 3
One of the list is exhausted. Adding the rest of one of the lists.
result now is [1, 2, 3, 4, 5, 6]
exiting mergesort on [6, 5, 4, 3, 2, 1]
#---
Merge sort всегда был одним из моих любимых алгоритмов.
вы начинаете с коротких отсортированных последовательностей и продолжаете объединять их по порядку в более крупные отсортированные последовательности. Столь простой.
рекурсивная часть означает, что вы работаете в обратном направлении - начиная со всей последовательности и сортируя две половины. Каждая половина также разделяется, пока сортировка не станет тривиальной, когда в последовательности есть только ноль или один элемент. В качестве функции recursed вернуть отсортированный последовательности сделать больше, как я и сказал в первоначальном описании.
несколько способов помочь себе понять это:
шаг через код в отладчике и посмотреть, что происходит. Или, Пройдите через него на бумаге (с очень маленьким примером) и посмотрите, что произойдет.
(лично я считаю, что делать такие вещи на бумаге более поучительно)
концептуально это работает следующим образом:
Входной список продолжает дробиться на все меньшие и меньшие части, будучи вдвое меньше (например,list[:middle] Это первая половина). Каждая половина делится пополам снова и снова, пока его длина не станет меньше 2. Т. е. до тех пор, пока это вообще ничего или один элемент. Эти отдельные части затем объединяются с помощью процедуры слияния, добавляя или чередуя 2 sub-списка в result list, и, следовательно, вы получаете отсортированный список. Поскольку 2 под-списка должны быть отсортированы, добавление / чередование является быстрым (O (n) операции).
ключ к этому (на мой взгляд) не является процедурой слияния, что довольно очевидно один раз вы понимаете, что входы в него всегда будут отсортированы. "Трюк" (я использую кавычки, потому что это не трюк, это компьютерная наука:-) ) заключается в том, что для того, чтобы гарантировать, что входные данные для слияния отсортированы, вы должны продолжать рекурсировать вниз, пока не доберетесь до списка, который должны сортироваться, и именно поэтому вы продолжаете рекурсивно вызывать mergesort до тех пор, пока список не будет меньше 2 элементов.
рекурсия и по расширению сортировки слияния могут быть неочевидными, когда вы впервые пришли поперек них. Вы можете обратиться к хорошей книге алгоритмов (например,DPV доступен онлайн, легально и бесплатно), но вы можете получить долгий путь, пройдя через код, который у вас есть. Если вы действительно хотите попасть в Стэнфорд / Coursera algo курс скоро снова работает, а он покрывает сортировка слиянием мелких деталей.
Если вы действительно хотите понять, прочитайте главу 2 этой книги, а затем выбросьте код, приведенный выше и переписать с нуля. Серьезно.
в основном вы получаете свой список, затем вы разделяете его, а затем сортируете его, но вы применяете этот метод рекурсивно, чтобы в конечном итоге разбить его снова и снова, пока у вас нет тривиального набора, который вы можете легко сортировать, а затем объединить все простые решения, чтобы получить полностью отсортированный массив.
вы можете иметь хорошую визуализацию о том, как сортировка слиянием работает здесь:
http://www.ee.ryerson.ca / ~courses/coe428/sorting/mergesort.html
надеюсь, это поможет.
Как Википедия статья объясняет, Есть много ценных способов выполнить сортировку слияния. Способ выполнения слияния также зависит от коллекции вещей, которые должны быть объединены, определенных коллекций, позволяющих определенные инструменты, которые коллекция имеет в своем распоряжении.
Я не собираюсь отвечать на этот вопрос с помощью Python, просто потому, что я не могу его написать; однако, принятие части алгоритма "сортировки слияния", похоже, действительно находится в центре вопроса, в большой. Ресурс, который помог мне, - это довольно устаревший K. I. T. E страница по алгоритму (написанному профессором), просто потому, что автор контента исключает контекст-осмысленные идентификаторы.
мой ответ получен из этого ресурса.
помните, алгоритмы сортировки слияния работают, разбирая предоставленную коллекцию, а затем снова складывая каждую из отдельных частей вместе, сравнивая части друг с другом как коллекция перестроена.
вот " код "(посмотрите в конец для Java "скрипки"):
public class MergeSort {
/**
* @param a the array to divide
* @param low the low INDEX of the array
* @param high the high INDEX of the array
*/
public void divide (int[] a, int low, int high, String hilo) {
/* The if statement, here, determines whether the array has at least two elements (more than one element). The
* "low" and "high" variables are derived from the bounds of the array "a". So, at the first call, this if
* statement will evaluate to true; however, as we continue to divide the array and derive our bounds from the
* continually divided array, our bounds will become smaller until we can no longer divide our array (the array
* has one element). At this point, the "low" (beginning) and "high" (end) will be the same. And further calls
* to the method will immediately return.
*
* Upon return of control, the call stack is traversed, upward, and the subsequent calls to merge are made as each
* merge-eligible call to divide() resolves
*/
if (low < high) {
String source = hilo;
// We now know that we can further divide our array into two equal parts, so we continue to prepare for the division
// of the array. REMEMBER, as we progress in the divide function, we are dealing with indexes (positions)
/* Though the next statement is simple arithmetic, understanding the logic of the statement is integral. Remember,
* at this juncture, we know that the array has more than one element; therefore, we want to find the middle of the
* array so that we can continue to "divide and conquer" the remaining elements. When two elements are left, the
* result of the evaluation will be "1". And the element in the first position [0] will be taken as one array and the
* element at the remaining position [1] will be taken as another, separate array.
*/
int middle = (low + high) / 2;
divide(a, low, middle, "low");
divide(a, middle + 1, high, "high");
/* Remember, this is only called by those recursive iterations where the if statement evaluated to true.
* The call to merge() is only resolved after program control has been handed back to the calling method.
*/
merge(a, low, middle, high, source);
}
}
public void merge (int a[], int low, int middle, int high, String source) {
// Merge, here, is not driven by tiny, "instantiated" sub-arrays. Rather, merge is driven by the indexes of the
// values in the starting array, itself. Remember, we are organizing the array, itself, and are (obviously
// using the values contained within it. These indexes, as you will see, are all we need to complete the sort.
/* Using the respective indexes, we figure out how many elements are contained in each half. In this
* implementation, we will always have a half as the only way that merge can be called is if two
* or more elements of the array are in question. We also create to "temporary" arrays for the
* storage of the larger array's elements so we can "play" with them and not propogate our
* changes until we are done.
*/
int first_half_element_no = middle - low + 1;
int second_half_element_no = high - middle;
int[] first_half = new int[first_half_element_no];
int[] second_half = new int[second_half_element_no];
// Here, we extract the elements.
for (int i = 0; i < first_half_element_no; i++) {
first_half[i] = a[low + i];
}
for (int i = 0; i < second_half_element_no; i++) {
second_half[i] = a[middle + i + 1]; // extract the elements from a
}
int current_first_half_index = 0;
int current_second_half_index = 0;
int k = low;
while (current_first_half_index < first_half_element_no || current_second_half_index < second_half_element_no) {
if (current_first_half_index >= first_half_element_no) {
a[k++] = second_half[current_second_half_index++];
continue;
}
if (current_second_half_index >= second_half_element_no) {
a[k++] = first_half[current_first_half_index++];
continue;
}
if (first_half[current_first_half_index] < second_half[current_second_half_index]) {
a[k++] = first_half[current_first_half_index++];
} else {
a[k++] = second_half[current_second_half_index++];
}
}
}
У меня также есть версия, здесь, который будет выводить полезную информацию и дать более наглядное представление о том, что происходит выше. Подсветка синтаксиса также лучше, если это полезно.
картинка стоит тысячи слов, а анимация стоит 10,000.
Checkout следующая анимация взята из Википедия это поможет вам визуализировать, как на самом деле работает алгоритм сортировки слиянием.
полная анимации с объяснением для каждого шага в процессе сортировки для любознательных.
другое интересные анимации различных типов алгоритмов сортировки.