определитель матрицы дифференцирования в tensorflow

меня интересует вычисление производной матричного детерминанта с использованием TensorFlow. Из экспериментов я вижу, что TensorFlow не реализовал метод дифференцирования через определитель:

LookupError: No gradient defined for operation 'MatrixDeterminant' 
(op type: MatrixDeterminant)

небольшое дальнейшее исследование показало, что на самом деле можно вычислить производную; см., например,формула Якоби. Я определил, что для реализации этого средства дифференцирования через определитель, который мне нужно используйте функцию декоратора,

@tf.RegisterGradient("MatrixDeterminant")
def _sub_grad(op, grad):
    ...

однако я недостаточно знаком с тензорным потоком, чтобы понять, как это может быть достигнуто. У кого-нибудь есть какие-нибудь соображения на этот счет?

вот пример, где я сталкиваюсь с этой проблемой:

x = tf.Variable(tf.ones(shape=[1]))
y = tf.Variable(tf.ones(shape=[1]))

A = tf.reshape(
    tf.pack([tf.sin(x), tf.zeros([1, ]), tf.zeros([1, ]), tf.cos(y)]), (2,2)
)
loss = tf.square(tf.matrix_determinant(A))


optimizer = tf.train.GradientDescentOptimizer(0.001)
train = optimizer.minimize(loss)

init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)


for step in xrange(100):
    sess.run(train)
    print sess.run(x)
6
determinants python tensorflow

3 ответов

пожалуйста, проверьте раздел "реализовать градиент в Python"здесь

в частности, вы можете реализовать это следующим образом

@ops.RegisterGradient("MatrixDeterminant")
def _MatrixDeterminantGrad(op, grad):
  """Gradient for MatrixDeterminant. Use formula from 2.2.4 from
  An extended collection of matrix derivative results for forward and reverse
  mode algorithmic differentiation by Mike Giles
  -- http://eprints.maths.ox.ac.uk/1079/1/NA-08-01.pdf
"""
  A = op.inputs[0]
  C = op.outputs[0]
  Ainv = tf.matrix_inverse(A)
  return grad*C*tf.transpose(Ainv)

затем простой цикл обучения, чтобы проверить, что он работает:

a0 = np.array([[1,2],[3,4]]).astype(np.float32)
a = tf.Variable(a0)
b = tf.square(tf.matrix_determinant(a))
init_op = tf.initialize_all_variables()
sess = tf.InteractiveSession()
init_op.run()

minimization_steps = 50
learning_rate = 0.001
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
train_op = optimizer.minimize(b)

losses = []
for i in range(minimization_steps):
  train_op.run()
  losses.append(b.eval())

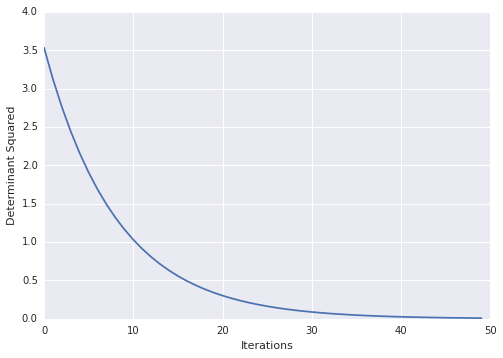
тогда вы можете визуализировать свои потери с течением времени

import matplotlib.pyplot as plt

plt.ylabel("Determinant Squared")
plt.xlabel("Iterations")
plt.plot(losses)

должен увидеть что-то вроде этого Loss plot

8

Я думаю, что вы путаете с тем, что такое производная матричного детерминанта.

матричный определитель-это функция, которая вычисляется по элементам матрицы по некоторой формуле. Поэтому, если все элементы матрицы являются числами, вы определителем будете вы только одно число и производная будет 0. Когда некоторые из элементов являются переменными, вы получите выражение этих переменных. Например:

x, x^2
1, sin(x)

в определителем будет x*sin(x) - x^2 и производное 2x + sin(x) + x*cos(x). Формула Якоби просто соединяет определитель с вспомогательной матрицей.

в вашем примере ваша матрица A состоит только из чисел, и поэтому определителем является только число и loss - это просто число, а также. GradientDescentOptimizer необходимо иметь некоторые свободные переменные для минимизации и не имеет, потому что ваш loss - это просто число.

0

для тех, кто заинтересован, я обнаружил решение, которое работает над моими проблемами:

@tf.RegisterGradient("MatrixDeterminant")
def _MatrixDeterminant(op, grad):
    """Gradient for MatrixDeterminant."""
    return op.outputs[0] * tf.transpose(tf.matrix_inverse(op.inputs[0]))
0