Оптимизация Hyperparameter для глубокого изучения конструкций с использованием Байесовской оптимизации

хотя я все еще не полностью понимаю оптимизацию алгоритм, я питаюсь, как будто он мне очень поможет.

во-первых, позвольте мне вкратце объяснить эту часть. Байесовские методы оптимизации направлены на решение проблемы поиска-разработки компромисса в проблема многоруких бандитов. В этой проблеме есть неизвестный функция, которую мы можем оценить в любой точке, но каждая оценка стоит (прямой штраф или издержки), и цель состоит в том, чтобы найти ее максимум, используя как можно меньше попыток. В принципе, компромисс таков: вы знаете функцию в конечном наборе точек (из которых некоторые хорошие, а некоторые плохие), поэтому вы можете попробовать область вокруг текущего локального максимума, надеясь улучшить ее (эксплуатация), или вы можете попробовать совершенно новую область пространства, которая потенциально может быть намного лучше или намного хуже (исследование), или где-то между ними.

методы Байесовской оптимизации (например PI, EI, UCB), построить модель целевой функции с помощью Процесс Гауссовский (GP) и на каждом шаге выбирают наиболее "перспективную" точку на основе их модели GP (обратите внимание, что "перспективные" могут быть определены по-разному различными конкретными методами).

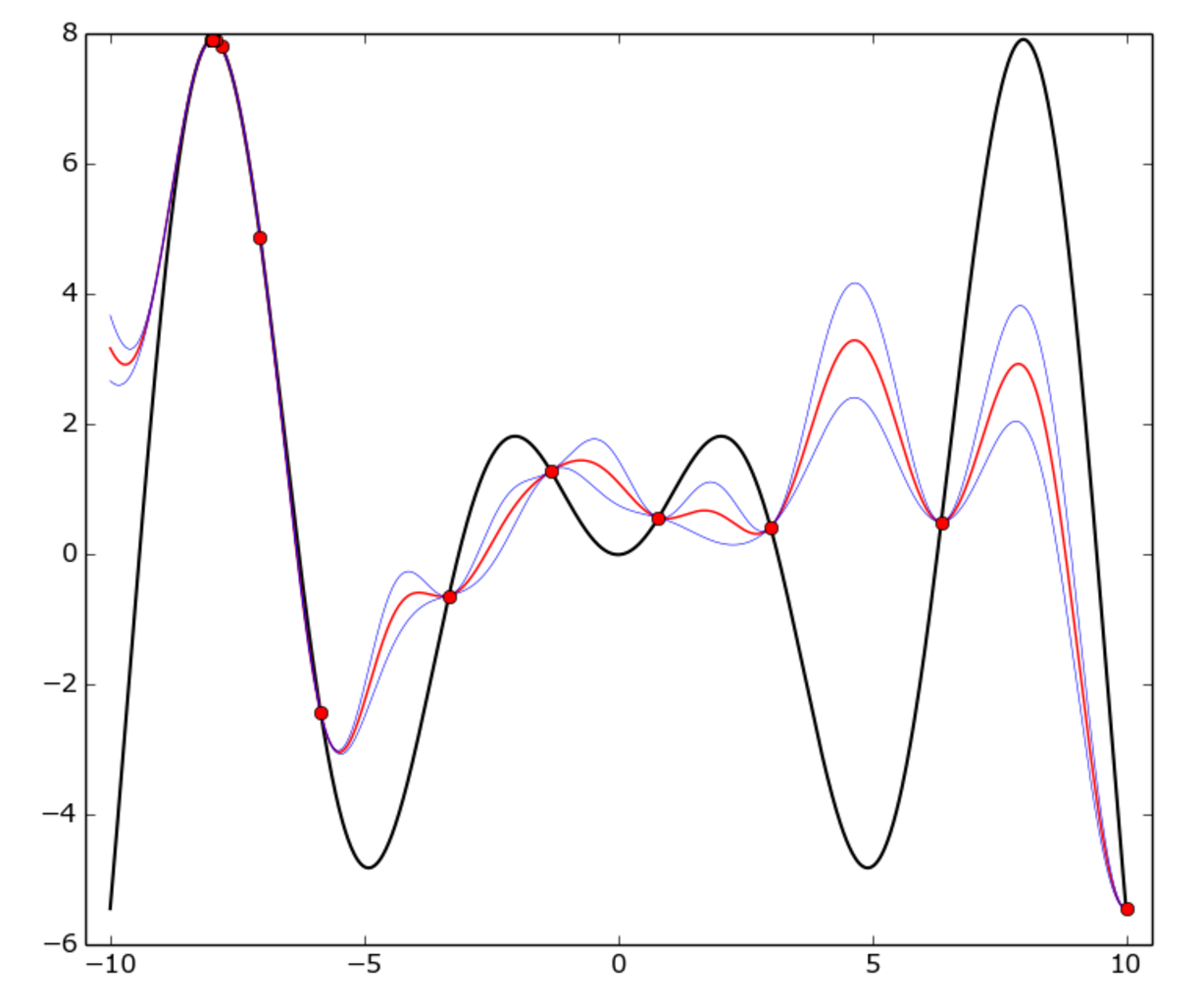
вот пример:

истинная функция f(x) = x * sin(x) (черная кривая) on [-10, 10] интервал. Красные точки представляют каждое испытание, красная кривая GP mean, синяя кривая-это средний плюс или минус один стандартное отклонение. Как вы можете видеть, модель GP не везде соответствует истинной функции, но оптимизатор довольно быстро определил "горячую" область вокруг -8 и начал его эксплуатировать.

как настроить байесовскую оптимизацию в отношении глубокого сеть?

в этом случае пространство определяется (возможно, преобразованными) гиперпараметрами, обычно многомерный единичный гиперкуб.

например, предположим, что у вас есть три гиперпараметра: скорость обучения α in [0.001, 0.01], регуляризатор λ in [0.1, 1] (как непрерывный), так и скрытый размер слоя N in [50..100] (целое число). Пространство для оптимизации-это 3-мерный куб [0, 1]*[0, 1]*[0, 1]. Каждый пункт (p0, p1, p2) в этом кубе соответствует Троице (α, λ, N) следующие преобразования:

p0 -> α = 10**(p0-3)
p1 -> λ = 10**(p1-1)
p2 -> N = int(p2*50 + 50)

какова функция, которую я пытаюсь оптимизировать? Это стоимость этот проверка установлена после N эпох?

правильно, целевая функция-точность проверки нейронной сети. Понятно, что каждая оценка стоит дорого, потому что для обучения требуется как минимум несколько эпох.

также обратите внимание, что целевая функция случайные, т. е. две оценки в одной и той же точке могут немного отличаться, но это не блокатор для Байесовской оптимизации, хотя это, очевидно, увеличивает неопределенность.

мята является хорошей отправной точкой для этой задачи? Любой другой предложения для этой задачи?

мята хорошая библиотека, вы можете определенно работать с этим. Я также могу рекомендовать hyperopt.

в моих собственных исследованиях я закончил писать свою собственную крошечную библиотеку, в основном по двум причинам: я хотел использовать точный Байесовский метод (в частности, я нашел портфолио UCB и PI сошлись быстрее, чем что-либо еще, в моем случае); плюс есть еще одна техника, которая может сэкономить до 50% времени обучения под названием предсказание кривой обучения (идея в том, чтобы пропустить полный цикл обучения, когда оптимизатор уверен, модель не учится так быстро, как в других областях). Я не знаю никакой библиотеки, которая реализует это, поэтому я закодировал ее сам, и в конце концов это окупилось. Если вам интересно, код на GitHub.