Пересечение Окружности Отрезка Линии
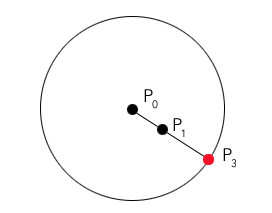
Я пытаюсь определить точку, в которой отрезок линии пересекаются окружности. Например, учитывая любую точку между P0 и P3 (а также предполагая, что вы знаете радиус), какой самый простой способ определить P3?
5 ответов
у вас есть система уравнений. Круг определяется: x^2 + y^2 = r^2. Линии определяется y = y0 + [(y1 - y0) / (x1 - x0)]·(x - x0). Подставьте вторую в первую, вы получите x^2 + (y0 + [(y1 - y0) / (x1 - x0)]·(x - x0))^2 = r^2. Решите это, и вы получите значения 0-2 для x. Подключите их обратно в любое уравнение, чтобы получить ваши значения для y.
как правило,
- найти угол между P0 и P1
- нарисуйте линию под этим углом от P0 на расстоянии r, что даст вам P3
в псевдокоде,
theta = atan2(P1.y-P0.y, P1.x-P0.x)
P3.x = P0.x + r * cos(theta)
P3.y = P0.y + r * sin(theta)
из центра круга и радиуса вы можете написать уравнение, описывающее круг. Из двух точек P0 и P1 можно написать уравнение, описывающее линию.
таким образом, у вас есть 2 уравнения в 2 неизвестных, которые вы можете решить путем замены.
Let (x0,y0) = координаты точки P0
и (x1,y1) = координаты точки P1
и r = радиус круг.
уравнение для круга:
(x-x0)^2 + (y-y0)^2 = r^2
уравнение для строка:
(y-y0) = M(x-x0) // where M = (y1-y0)/(x1-x0)
подключение 2-го уравнения в первое, получим:
(x-x0)^2*(1 + M^2) = r^2
x - x0 = r/sqrt(1+M^2)
аналогично вы можете найти, что
y - y0 = r/sqrt(1+1/M^2)
точка (x,y) - это точка пересечения между линией и кругом, (x,y) - ваш ответ.
P3 = (x0 + r/sqrt(1+M^2), y0 + r/sqrt(1+1/M^2))
перейти к этому коду..его сэкономить время
private boolean circleLineIntersect(float x1, float y1, float x2, float y2, float cx, float cy, float cr ) {
float dx = x2 - x1;
float dy = y2 - y1;
float a = dx * dx + dy * dy;
float b = 2 * (dx * (x1 - cx) + dy * (y1 - cy));
float c = cx * cx + cy * cy;
c += x1 * x1 + y1 * y1;
c -= 2 * (cx * x1 + cy * y1);
c -= cr * cr;
float bb4ac = b * b - 4 * a * c;
if(bb4ac<0){
return false; // No collision
}else{
return true; //Collision
}
}
КОД MATLAB
функция [ флаг] = circleLineSegmentIntersection2 (Ax, Ay, Bx, By, Cx, Cy, R)
% A и B - две конечные точки отрезка линии, а C-центр окружность, % R-радиус окружности. Эта вычислительная функция ближайшая точка fron C к сегменту %, если расстояние до ближайшая точка > R возврат 0 else 1
Dx = Bx-Ax;
Dy = By-Ay;
LAB = (Dx^2 + Dy^2);
t = ((Cx - Ax) * Dx + (Cy - Ay) * Dy) / LAB;
if t > 1
t=1;
elseif t<0
t=0;
end;
nearestX = Ax + t * Dx;
nearestY = Ay + t * Dy;
dist = sqrt( (nearestX-Cx)^2 + (nearestY-Cy)^2 );
if (dist > R )
flag=0;
else
flag=1;
end
конец
